XPNAV-1卫星先期发布数据的计时分析

朱鸿旭，童明雷，杨廷高，赵成仕，李 琳，高玉平

(1. 中国科学院国家授时中心，西安 710600；2. 中国科学院时间频率基准重点实验室，西安 710600；3. 中国科学院大学，北京 100049)

0 引言

脉冲星是自转非常稳定的自然天体，通常具有从射电一直到Gamma射线的多波段电磁辐射。而毫秒脉冲星由于自转稳定性更高，更值得我们关注。对毫秒脉冲星的计时观测，在科学和工程上有诸多应用。利用地面上的射电望远镜对脉冲星做长期计时观测，可以开展脉冲星时间尺度建立[1-3]、探测低频引力波[4-7]、测量太阳系行星质量[8]等方面的研究工作。利用X射线脉冲星可以实现各类空间飞行器自主导航，尤其适用于深空探测飞行器导航。理论上，若星载原子钟精度足够高，同时观测三颗脉冲星即可对航天器展开绝对导航。在观测多颗脉冲星相对困难的情况下，还可以利用脉冲星进行相对导航[9]。目前，深空探测飞行器导航主要依赖地面跟踪测量技术，如美国的深空跟踪网(Deep space network,DSN)或甚长基线干涉测量(Very long baseline interferometry,VLBI)技术。由于深空探测飞行器距离地球遥远，信号延迟大(如1AU距离，信号延迟约8.5 min，探测冥王星飞行器信号延迟达到约4 h)，不能做到实时定位测量。另外，地面跟踪测量精度随着飞行器距离增大而降低。脉冲星作为宇宙中的自然天体，当其自转参数(自转频率及其导数)与天体测量参数(方向，距离与自行)经过精确测定后，可以为太阳系范围内各类飞行器进行导航，其导航精度与飞行器距离无关。另外，脉冲星也有可能用作卫星导航的备用或辅助导航手段以及某些特殊情况下的自主导航[10-11]。2004年Sheikh[12]、Sala等[13]基于现代卫星导航系统体制的思想，各自论证了基于X射线脉冲星航天器自主导航的可行性。自此，各国脉冲星自主导航的相关研究进入快轨道[14-19]。尤其随着美国NICER/SEXTANT项目成功运行，脉冲星导航的可实现性与可操作性受到越来越广泛的认可[20]。我国在X射线脉冲星导航领域近几年也发展迅速。硬X射线调制望远镜(HXMT/慧眼卫星)、天宫二号搭载的POLAR、X射线脉冲星导航试验卫星(XPNAV-1)等平台均在进行X射线观测，开展了脉冲星导航试验，并取得了一系列进展和成果[21-24]。对于脉冲星导航而言，Crab脉冲星是这些X射线观测任务的一个主要目标源。

Crab脉冲星是公元1054年超新星爆发的产物[25]，它的X射线波段辐射在所有脉冲星中最强。由于Crab脉冲星比较年轻，内部物理过程仍频繁发生，导致其自转不稳定，需要每月甚至更频繁地更新自转参数。但由于Crab脉冲星具有全波段的辐射，且流量很强，便于观测、分析。因此，利用卫星对Crab脉冲星展开持续观测，进行脉冲星导航试验仍是很有必要的。

目前我国的天基脉冲星导航试验均基于人造地球卫星开展，今后可能会基于其他天体卫星(如：人造火星卫星)展开试验，并应用于深空探测飞行器。对于人造卫星而言，若利用脉冲星对其进行自主导航，目前比较成熟的是基于轨道动力学[21]与X射线脉冲星计时观测相结合的Kalman滤波[26-27]的方法。Kalman滤波的状态方程包括轨道动力学模型及星载原子钟的状态方程；Kalman滤波的测量方程即为脉冲星计时观测[28]。更重要的是建立卫星的轨道动力学模型，一般包括地球(火星)中心引力以及对应非球形摄动力模型。若对地球卫星进行导航，第三体主要考虑太阳与月亮的影响。对于低轨道卫星，还应该建立大气阻力模型。由此可见，若对人造卫星进行脉冲星导航，对地球(火星)重力场展开精确测量显得尤为重要[29-30]。高精度动力学模型有利于卫星轨道预报。但动力学模型的误差具有累积性，会导致卫星轨道位置偏离越来越大。因而需要依赖外部观测手段，如脉冲星计时观测，实时测量卫星的轨道位置。设计合适的Kalman滤波器，在滤波器内将动力学预报与脉冲星计时观测结合起来，从而实现具有一定精度的卫星轨道位置的预报与更新。如果知道卫星的多普勒频移信息，可以将其与前述信息进行融合以提高导航精度[31]。根据XPNAV-1卫星轨道参数特征，理论上，利用轨道动力学模型与Crab脉冲星观测，可以验证Kalman滤波方法精度。但XPNAV-1观测Crab脉冲星35组数据时间跨度为31天，如果由每组观测，计算得到一个TOA(TimE-of-artival)，在删除错误观测后，实际上平均每天约只有一个有效TOA测量值。1天内卫星绕卫星轨道运动大约近20圈。利用如此稀疏的测量数据，估计难以用Kalman滤波方法直接检验XPNAV-1导航精度。而在测量方程中，TOA的测量精度和脉冲星计时模型精度是影响脉冲星导航精度的两个重要因素。如果脉冲到达时刻的测量和脉冲星计时模型的精度都很高，那么二者之差(计时残差)也会很小。因此，计时残差的大小对脉冲星导航的精确度有着根本的影响：计时残差的标准差σ每增大10 μs，导航精度至少下降3 km。不仅如此，获得X射线脉冲星的计时残差，是构建天基授时系统的基础，对建立综合脉冲星时同样有着深远的意义。

鉴于此，本文将对XPNAV-1先期发布的35组Crab脉冲星观测数据[32]进行计时精度分析，每组数据观测积分时间为50 min左右。XPNAV-1搭载了两种不同体制的X射线探测器，工作能谱为0.5～10 keV[22]。首先将观测数据时间尺度由UTC(Universal time coordinated)时间尺度转换为质子力学时(TDB)时间尺度，同时采用英国Jordrell Bank台发布的Crab脉冲星星历[33-34]与美国JPL发布的DE200历表[35]将光子到达卫星时刻转换至太阳系质心(Solar system barycenter,SSB)。随后利用35组数据建立积分脉冲轮廓与标准脉冲轮廓并进行互相关处理，得到观测的脉冲到达时刻(TOA)。再与Crab脉冲星模型参数预报的TOA作差得到计时残差。

1 光子到达时刻转换与脉冲轮廓建立

对于X射线脉冲星计时观测而言，要获得TOA，通常需要先将光子达到航天器时刻转换到达到SSB的时刻，然后进行周期折叠建立积分脉冲轮廓，再与标准脉冲轮廓进行互相关，得到TOA。当然，也可以采用美国SEXTANT脉冲星导航试验观测脉冲星的处理方法。该方法利用最大似然估计，直接由观测记录的光子到达时刻序列数据，计算得到脉冲星脉冲到达探测器时刻与多普勒频移两个参数[36]。鉴于目前XPNAV-1公开发布的数据脉冲信噪比有限，因此本文仍采取将光子到达时刻转换到SSB并进行轮廓折叠的方法。

先期发布的数据中，每组观测包括卫星接收到Crab光子的时刻文件和遥测的轨道文件。由于光子到达卫星时刻与进行轨道遥测的时刻并不重合，因此需要将轨道位置与速度内插到光子到达卫星时刻。利用观测期间对应的Crab脉冲星星历与DE历表，将光子到达时刻由卫星转换到SSB。转换方程为：

Δ☉=ΔE☉+ΔR☉+ΔS☉

(1)

式中：Δ☉表示光子到达时刻转换到SSB产生的总延迟量；ΔE☉表示Einstein延迟，表示时间尺度转换产生的延迟量；ΔR☉表示Roemer延迟，代表几何真空延迟；ΔS☉表示Shapiro延迟，代表时空弯曲引起的延迟。Jordrell Bank台80年代就开始发布Crab脉冲星星历。为了保证前后数据归算采用的参数一致，目前其给出的Crab脉冲星星历仍基于DE200历表与TDB时间尺度，且不包含视差与自行。因而在作时间转换时也必须与Crab脉冲星星历保持一致，使用DE200历表与TDB时间尺度，同样也不考虑视差与自行，以避免产生额外的误差。观测文件中光子达到时刻是用UTC时间尺度来记录的，需转换为TDB时间尺度。其他部分的展开式可参照文献[37]，下文主要给出UTC到TDB的时间尺度转换表达式：

ΔE☉=ΔTAI-UTC+ΔTT-TAI+ΔTCB-TT+ΔTDB-TCB

(2)

进一步展开，有[38-39]：

ΔTAI-UTC=l

(3)

ΔTT-TAI=32s.184+δ

(4)

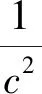
(5)

ΔTDB-TCB=-LBΔtTCB

(6)

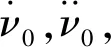
(7)

(8)

建立积分脉冲轮廓时，将每组观测第一个光子到达SSB的时刻作为起点(即积分脉冲轮廓的相位零点)，利用式(8)计算该组观测每个光子到达SSB时刻对应的Crab脉冲星自转相位φ1i，φ2i，…，φni，…。其中i表示某组观测，n表示该组观测的第n个光子。将每组观测的所有光子的相位都减去该组第一个光子相位φ1i再进行折叠。取归一化自转相位的小数值即为该光子所对应积分脉冲轮廓的相位值。将一个自转周期等分为N份，即为N个子相位间隔。N个子相位间隔与对应的光子数构成的直方图就是该组测量得到的积分脉冲轮廓。

标准脉冲轮廓由于要获得比积分脉冲轮廓更高的信噪比，因此，需利用全部可利用的观测资料进行折叠。折叠时，除统一以Crab脉冲星星历参数定义的相位零点为起点外，其余与积分脉冲轮廓折叠方法相同，且必须同样取N个相位间隔。折叠后的35组轮廓相加即得标准脉冲轮廓。图1、图2是当N=256时，得到的一组积分脉冲轮廓和利用全部35组观测资料得到的标准脉冲轮廓。

图1 某一组积分脉冲轮廓Fig.1 A set of integrated pulse profile

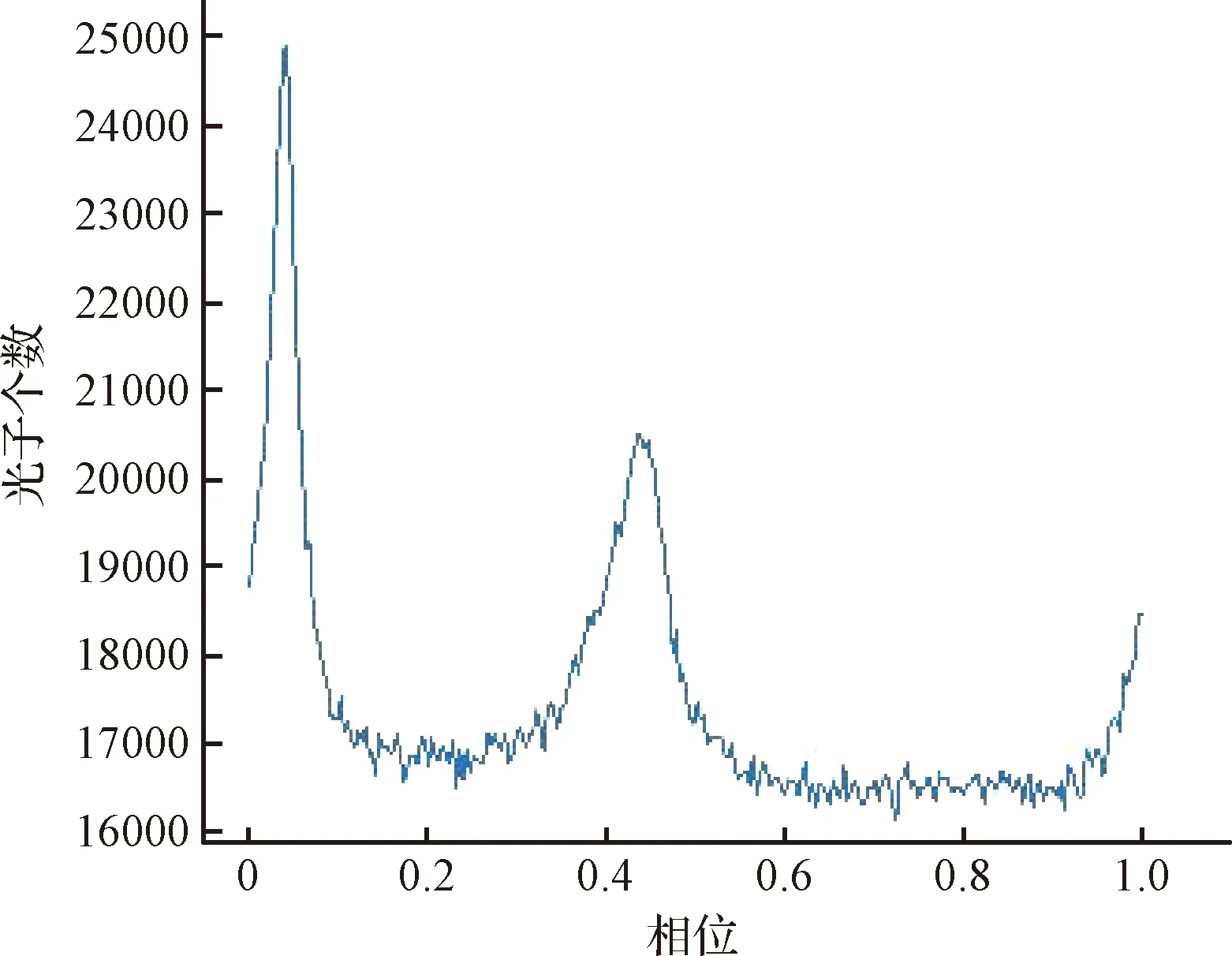
图2 标准脉冲轮廓Fig.2 Standard pulse profile

一般定义脉冲轮廓的主峰顶点对应的时刻标记为TOA。Crab脉冲星星历定义脉冲轮廓的主峰顶点为相位零点，即式(8)中的φ0=0。由图2可见，标准脉冲轮廓主峰顶点并不在相位零点，而是略有偏差，该相位差Δφ对应的时间差Δtφ约1.38 ms。这是由于两种不同的观测频段引起的零点相位差。因为Crab脉冲星在射电波段流量更强，观测得到的脉冲信噪比更高，故Jodrell Bank提供的星历基于射电波段给出。由于Crab脉冲星的轮廓随观测频段变化而有所不同[41]，当获得Crab脉冲星星历所使用的观测波段(射电)与卫星探测光子的频段(X射线)不一致时，利用星历折叠出的脉冲轮廓主峰顶点会产生相位差。一般认为，不同波段的光子是由脉冲星不同位置辐射出的[42]。因此，当用X射线脉冲星导航，而其星历参数来自于射电波段观测的情况下，相位零点差的精确测量是非常必要的。

2 获得观测TOA与计时残差

每组积分脉冲轮廓分别与标准脉冲轮廓进行互相关计算可以获得二者之间的相位差，进而获得时间差，确定TOA。离散傅里叶变换(DFT)法是一种常用的相关方法[43]。由于DFT法不需要知道脉冲的统计信息，且计算精度只与脉冲轮廓的信噪比有关，而与子相位间隔无关。鉴于目前卫星观测的信噪比较低，导致N难以取很高的值，脉冲直接包含的频域信息也较少[44]。且由于未获取大量观测数据，较难得知脉冲的确切统计信息。因此，采用DFT法进行计算是合适的。

设s(t)，p(t)分别为按照上文方法求得的Crab脉冲星的标准脉冲轮廓和一组积分脉冲轮廓。其中0≤t≤P，P为Crab脉冲星的自转周期。二者关系可表示为[43]：

p(t)=a+bs(t-τ)+g(t)

(9)

式中:a为幅值差，b为比例因子，τ为时间延迟，g(t)为高斯白噪声。τ是最为关心的待求量。对上式两边分别作DFT，根据DFT的线性性质，有：

Pkexp(iθk)=aN+bSkexp[i(φk+2πνkτ)]+Gk

(10)

χ2(τ)=

(11)

(12)

由于待求量τ包含在三角函数内，难以直接求解。故一般用迭代方法求解。初值可以选择0值。为提高迭代效率，最好选择时域相关计算的τ。根据式(12)计算出的每组的τ，再加上每组观测第一个光子到达时刻即代表每组数据观测的TOA。

3 计时残差分析

脉冲星观测TOA与根据脉冲星星历参数预报的TOA之差即为计时残差。第2节计算得到了每组观测得到的TOA，将观测TOA代入式(8)中的t,利用Jodrell Bank给出的Crab自转参数，可计算得到观测TOA对应的相位残差。将相位残差除以观测时刻Crab的自转频率就得到以时间单位表示的计时残差，即自转模型预报TOA与观测TOA之差。

利用上述算法，归算N=256时35组观测的计时残差，结果如图3所示。由于脉冲的信噪比有限，有些组的观测出现了迭代不收敛的现象，计算出的计时残差很大。去掉在所有观测的计时残差中迭代不收敛的观测组，再去掉超过标准差±3σ以上的观测组构成有效观测数据。即去掉序号为2，5，9，14，15，18，25的共7组观测，有效观测为剩余的28组观测数据。减掉Δφ引起的Δtφ(1.38 ms)之后，计时残差的结果如图4所示。注意，图3和图4是拟合前计时残差，即不对脉冲星计时模型参数做拟合。

图3 所有观测数据的计时残差Fig.3 Timing residuals of all observed data

需要指出的是，当利用脉冲星数据处理软件Tempo2[46]进行光子到达时刻转换时，一般使用TCB时间尺度进行计算，与Crab脉冲星星历采用的时间尺度不一致，这样就产生了系统误差[47]。而本文在做时间尺度转换时，未利用TEMPO2软件，而是采用了Python环境下的Astropy[47]等包，并采用了TDB时间尺度计算，避免了由时间尺度不一致导致的系统误差。如式(6)所示，这种误差以线性趋势项为主。

基于Crab脉冲星的导航试验还必须使用定期更新的星历，以及与归算星历时一致的太阳系历表。英国Jodrell Bank提供的Crab脉冲星星历定期更新，且在目前精确度最高。然而，该星历基于DE200历表给出，其发布时间很早，误差较大。所提供的各天体的位置与较新的历表(如DE430)约有数百公里的差，且带有明显的趋势项。若使用DE430历表归算，尽管其自身的精确度高于DE200历表，但由于与归算脉冲星星历使用的历表不同，采用同样的数据处理方法，结果得到的计时残差比采用DE200历表的计时残差反而弥散度更大。另外，英国Jodrell Bank天文台提供的Crab脉冲星星历没有给出Crab脉冲星的自行与视差参数，在数据处理时又试验性地增加了该脉冲星的自行与视差参数(取自于国际脉冲星数据库)，结果也表明残差弥散变大。这证明，在脉冲星导航数据处理时，采用的脉冲星星历参数(包括自转参数与位置等天体测量参数)必须是内部自洽的一套参数，不能人为地增加或减少某些个别参数，否则会降低精度。采用与脉冲星星历相一致的DE历表与质心坐标时也同样是非常重要的，否则会产生系统误差。对于利用Crab脉冲星的导航试验研究，尽快利用中国的射电计时观测，实时提供高精度星历表是必要的。地面射电与空间X射线同步观测研究是非常有意义的。

上文以N=256为例，进行了试验，得到了上述结论。但N的取值未必是恰当的。依次取N=128～512，重复上述处理过程，可得到N与残差的RMS，及无效观测组数之间的关系。由图5可以看出，当N逐渐增加时，残差的RMS先线性降低，再基本保持平稳，后幅度剧烈变化。由于轮廓折叠等价于进行低通滤波，而观测的信噪比较低，于是当N过大时，滤波效果不明显，导致轮廓信噪比迅速降低；当N过小时，又会导致轮廓过平滑，导致频域信息缺失过多，影响相关计算结果。这与由图5得出的信息是一致的。因此，从实际应用的角度出发，对XPNAV-1的数据而言，取N=256是恰当的。

如图6所示，无效观测组数大致呈线性增加的趋势。尽管每次观测积分时间均为50 min左右，但由于卫星所在位置不同，受到的遮挡与干扰因素也不尽相同。故每次观测时的脉冲信噪比不一致。当N持续增大时，脉冲信噪比较差的观测滤波效果有限，从而导致相关计算过程中出现不收敛现象。对于XPNAV-1而言，需持续改进观测方案，提升有效观测时长，并尽可能减少背景光子的影响。同时，在积累了大量数据后，还可以利用先验知识，对TOA测量方法加以改进。这些都是提高TOA测量精度，增加有效观测数可行的手段。

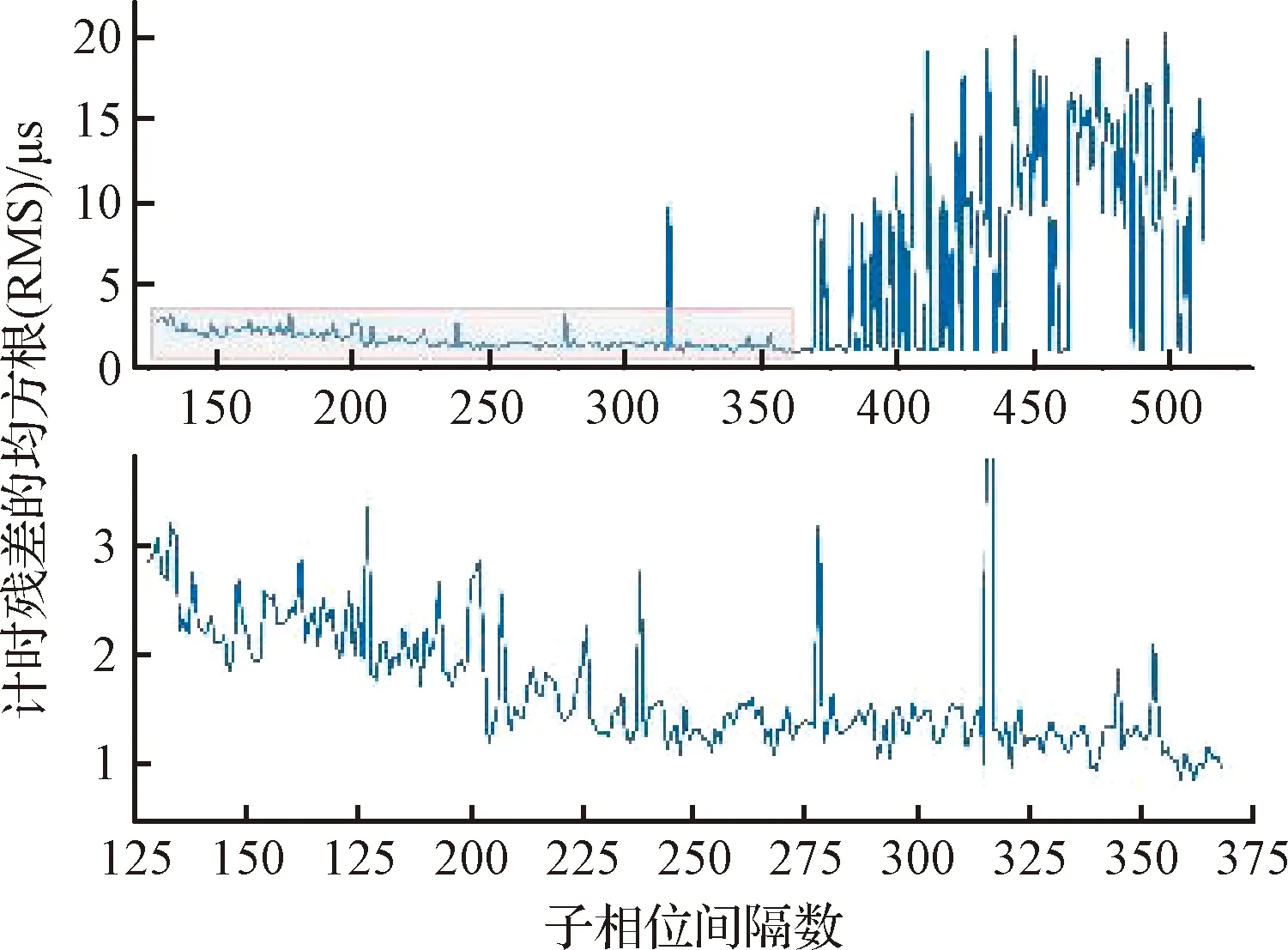
图5 子相位间隔数与残差均方根(RMS)的关系Fig.5 The relationship between the number of sub-phase intervals and the RMS of timing residuals

图6 相位间隔数与无效观测组数的关系Fig.6 The relationship between the number of sub-phase intervals and the number of unavailable observed data set

图7 两种取权方法的一组轮廓比较Fig.7 Comparison of a set of pulse profiles for two weighting methods

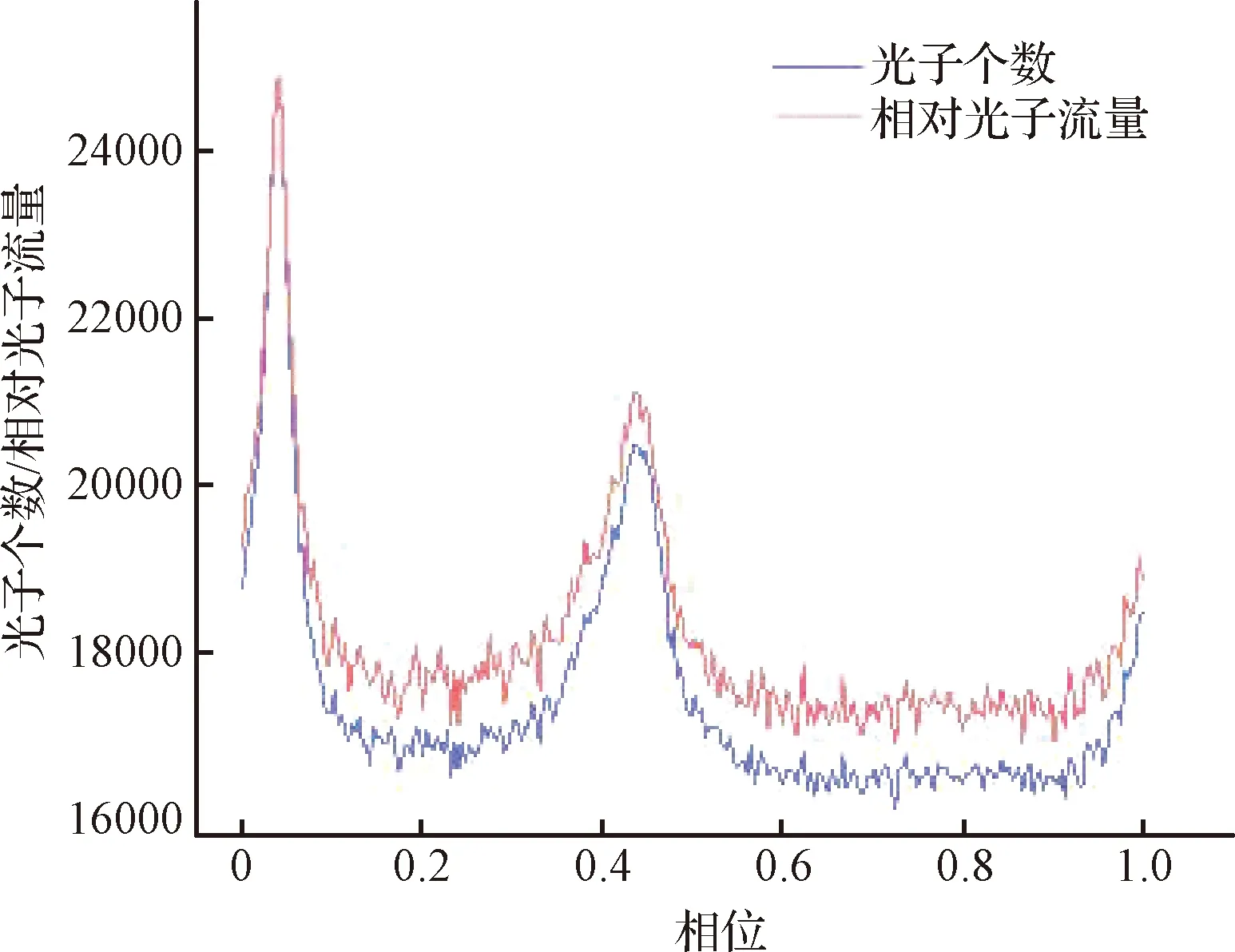
图8 两组取权方法的标准脉冲轮廓比较Fig.8 Comparison of standard pulse profiles for two weighting methods

4 结 论

本文利用Python环境下的Astropy包处理了XPNAV-1先期公布的35组观测数据，分别建立了积分脉冲轮廓和标准脉冲轮廓，采用DFT方法将二者做互相关处理获得了测量TOA及其测量误差σTOA。结合英国Jordrell Bank台发布的Crab脉冲星星历与美国JPL发布的DE200历表，进一步得到了拟合前计时残差。该残差不存在系统趋势项，从而验证了XPNAV-1观测数据的有效性。同时，我们分析了在目前观测条件下，建立脉冲轮廓时子相位间隔N的取值与计时残差的RMS之间的关系。我们发现N取256是合适的。N=256时，计时残差的RMS为1.14 μs。同时也表明在现有观测条件和数据量的情况下，适宜采用折叠-DFT相关法获得测量TOA。从而证明利用中国自主观测资料，采用合适数据处理方法，能够获得较高的X射线脉冲星计时精度。由于Crab脉冲星的星历由射电波段的观测给出，而测量的TOA来源于X射线波段的观测，这二者存在零点相位差。在这35组的观测时间段内，我们得到零点相位差约为0.04，对应的时间差约为1.38 ms。本文利用XPNAV-1发布的数据只讨论了计时精度，旨在验证观测数据的有效性和数据质量。

在构建标准脉冲轮廓时，本文采用了全部观测数据以提高信噪比。而Crab脉冲星的脉冲轮廓会随时间推移产生变化[49]。先期发布的观测数据时间跨度约为一个月，这种变化可以忽略。当获得大量数据后，如果采用全部观测数据构建标准脉冲轮廓，观测数据的时间跨度可能会对其信噪比的提升造成影响。采用多长时间段的数据建立高信噪比的标准脉冲轮廓也是值得研究的一个问题。