时间尺度上Nielsen方程的Mei对称性与守恒量
舒莲莲, 朱建青
(苏州科技大学数学科学学院, 江苏 苏州 215009)
Hilger于1988年提出时间尺度概念. Bohner和Peterson整理并出版了首本时间尺度理论的专著[1], 以及线性动力学方程[2], 随后众多学者对时间尺度这一领域深入研究[3-6]. 运用时间尺度上的动力学方程, 可以解决许多在实际问题中的建模问题, 如经济学[7]中, 将成本函数结合时间尺度上的微分方程, 所得结果可最大化提高企业未来的竞争力. 在医学[8]中, 骨重建可表示为Lemaire动力学模型, 简单的模型有助于观察到动力学的定性性质, 例如没有超调和回弹等, 在描述繁杂的数学科技语言中扮演重要角色.
1935年, 丹麦Nielsen教授得到一类运动微分方程-Nielsen方程[9]. 我国分析力学领域先驱者梅凤翔教授提出了Nielsen算子. 在分析力学中, Nielsen方程与Lagrange方程享有同等重要地位. 而在某些情况下, Nielsen方程更方便, 如文献[10]中表明使用Nielsen方程对电路系统进行建模, 运用到的计算方法比使用Lagrange方程建模更容易, 因此研究Nielsen方程的构造、解或约化等很有意义. 1918年, Noether提出Noether对称性[11]. 1979年, Lutzky提出Lie对称性[12]. 2000年, 梅凤翔教授在此基础上, 首次提出一种形式不变性[13], 并称为Mei对称性. Mei对称性导出动力学系统的守恒量推动了分析力学领域的发展[14-20]. 贾利群等学者利用Mei对称性寻求Nielsen方程的守恒量进行了详细研究[21-22]. 2008年,Bartosiewicz和Torres首次将力学系统的Noether对称性应用于时间尺度上[23]. 随后, 众多学者将目光转向此类研究方向[24-27], 孔楠给出了时间尺度上Lagrange系统Mei对称性定义和判据方程, 讨论了Mei对称性导致的多个Mei守恒量[28]. 翟相华研究了时间尺度上Birkhoff与Hamilton力学系统的Mei对称性与守恒量[29]. 本文运用Mei对称性寻求时间尺度上Nielsen方程的守恒量, 根据时间尺度上链式法则, 建立单自由度的Nielsen运动微分方程, 给出Nielsen方程的Mei对称性的定义和判据, 从而导出守恒量, 文章的结尾处用例子来说明应用.
1 时间尺度上的Nielsen方程
由文献[30], 时间尺度上一般完整系统的Lagrange方程是
(1)
为推导简便, 本文主要将单自由度的Nielsen方程作为研究对象.
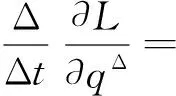
(2)
则方程(1)可表示为
(3)
因为Lagrange函数对t的Δ导数是
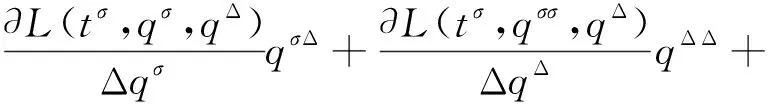
(4)
LΔ对qΔ的偏导数是

(5)
比较(3)与(5)式, 可得到
(6)
综上, 得出时间尺度上一般完整系统的Nielsen方程
(7)

2 时间尺度上Nielsen方程的Mei对称性和判据
N(L)=Q″.
(8)
时间尺度上的无限小变换
(9)
其中,ε为无限小参数,ξ0和ξ为无限小变换的生成元.在(9)的变换下, 函数L(t,qσ,qΔ)和Q″(t,qσ,qΔ)分别变为L*(t,(qσ)*,(qΔ)*)和Q″(t,(qσ)*,(qΔ)*).
定义1经过(9)式变换后动力学函数L和Q″分别被L*和Q″*所代替, (8)式的形式未改变, 即
N(L*)=Q″*,
(10)
则这样的不变性称为时间尺度上Nielsen方程的Mei对称性.
展开L*和Q″*, 有
L*=L*(t,(qσ)*,(qΔ)*)=
L(t,qσ,qΔ)+εX(1)(L)+o(ε2)
Q″*=Q″*(t,(qσ)*,(qΔ)*)=
Q″(t,qσ,qΔ)+εX(1)(Q″)+o(ε2),
(11)
其中,
(12)
将(11)式代入(10)式, 忽略ε2和更高阶的小量, 并联系 (8)式, 得到
N(X(1)(L))=Q″.
(13)
判据时间尺度上的Nielsen方程, 如若(9)式变换的无限小生成元ξ0和ξ满足 (13)式, 则对应的不变性称为其Mei对称性, (13)式被定为Mei对称性相应的判据方程.
3 时间尺度上Nielsen方程的Mei对称性与守恒量
定理1如若时间尺度上的Nielsen方程(7)的Mei对称性相应的生成元ξ0和ξ以及规范函数G=G(t,qσ,qΔ)满足以下条件
GΔ=0,
(14)
则Nielsen方程由Mei对称性得出的守恒量是
(15)
证明将式(15)两边对t求Δ-导数, 并利用方程(7)和式(14), 可得
GΔ=0.
(16)
证毕.
推论1当时间尺度T=, 则σ(t)=t,μ(t)=0, 于是由(15)式得出经典结构方程
(17)
得到经典力学下的Nielsen方程的Mei守恒量[21]
(18)
定理2如若时间尺度上的Nielsen方程(7)的Mei对称性的规范函数G=G(t,qσ,qΔ)和相应的生成元ξ0和ξ满足以下条件
(19)
则Nielsen方程Mei对称性得出的守恒量为
(20)
证明将式(20)两边对t求Δ-导数, 并利用方程(7)和式(14), 可得
qΔX(1)(Q″)+GΔ=0.
(21)
证毕.
推论2当时间尺度T=, 则σ(t)=t,μ(t)=0, 于是由(19)式得出经典结构方程
(22)
得到经典力学下的Nielsen方程的Mei守恒量
(23)
4 算例
例1在时间尺度T={2m+1:m∈N}上, Langrange函数为
(24)
分析Nielsen方程的Mei对称性相对应(15)式的Mei守恒量.
计算得到

(25)
将(24)式代入方程(7)得到:
2tqΔΔ+qΔ=1,
(26)
计算得到
(27)
取
(28)
则
X(1)(L)=-qσ,X(1)[X(1)(L)]=-1,
X(1)(Q″)=1.
(29)
将(28)式代入结构方程(14)中得到
G=t-tqΔ,
(30)
由(15)式可得Nielsen方程的守恒量
I=t-tqΔ.
(31)
例2在时间尺度Τ={3m+1:m∈N∪{0}}上, Langrange函数为
(32)
分析Nielsen方程的Mei对称性相对于(20)式的Mei守恒量.
计算得到

(33)
将(31)式代入方程(7)得:
2qΔΔ+1=0,
(34)
计算得到
(35)
取
(36)
则
(37)
将(35)式代入结构方程(19)中得到
G=qσ+2qΔ+t,
(38)
由(20)式可得Nielsen方程的守恒量
I=2qΔ+t.
(39)
5 结束语
时间尺度理论为统一连续、离散与量子等多样复杂的系统提供了重要的理论支撑, 为分析力学领域的发展, 越来越多的科研工作者关注并着手研究这一领域. 时间尺度上Nielsen方程的Mei对称性与守恒量是文章主要研究的问题, 由链式法则推导出时间尺度上Nielsen方程, 再设定Mei对称性的定义及判据, 从而得出来两个Mei守恒量. 当时间尺度退化到实数域时, 该守恒量可退化到经典Nielsen方程的守恒量, 并通过例子说明结果的有效性. 在时间尺度上运用对称性方法寻找动力学微分方程的守恒量, 是个灵活有效且变通性较强的方法, 未来研究可将本文时间尺度上Mei对称性的思想方法应用于不同类型的动力学方程.

