时间尺度上变质量非完整系统相对于非惯性系的Noether 对称性
方 蕊,朱建青
(苏州科技大学 数学科学学院,江苏 苏州 215009)
力学系统的对称性与守恒量在数学、物理等领域具有重要的研究意义,是分析力学的一个重要研究方向.许多学者研究力学系统的对称性和守恒量,并取得了一些研究成果[1-8].在研究经典力学系统时,往往需要对于离散系统和连续系统分开进行研究,如何让将两者统一起来进行研究成为了一个研究问题.时间尺度是测度链的一种,通过选取不同的时间尺度,可以得到更普遍的结果.时间尺度理论可以将离散系统、连续系统等统一起来进行研究,不仅避免了对于同一问题的重复研究,同时可以更深刻地揭示出力学系统之间的本质差异.自时间尺度理论被提出以来,已经在经济学、物理学、生物学、最优控制等许多领域得到了广泛应用[9-11].在时间尺度上研究力学系统的对称性和守恒量具有重要的意义,已有一些学者对于此方面进行了研究,并取得了一系列的研究成果[12-21].
随着科学技术的发展,航天技术也在不断发展,火箭和航空飞机等都是变质量系统,变质量系统的研究日益重要.近年来,一些学者对于非完整系统相对于非惯性系的对称性进行了研究.1992 年,罗绍凯[22]给出了变质量非完整系统相对于非惯性系的方程,随后罗绍凯和苏正雷研究了变质量非完整系统相对于非惯性系的Noether 对称性[23].目前已经有一些学者在时间尺度上对于变质量系统的对称性进行了一些研究,主要有时间尺度上变质量完整系统和非完整系统的Lie 对称性和守恒量2 个研究成果[24-25].本文区别于以往研究成果,在时间尺度上对于相对于非惯性系的变质量非完整的Noether 对称性与守恒量进行了研究,给出Noether 广义准对称性的判据和守恒量,对守恒量进行了证明,并举例说明研究结果的应用.
1 时间尺度上变质量非完整系统相对于非惯性系的运动方程
假设力学系统由n个广义坐标qs(s=1,2,···,n) 组成,在t时刻,第i个质点的质量为mi(i=1,2,···,N),在t+Δt时刻,质点并入或分离的质量为 Δmi,其中质点的质量可表示为

系统的运动受g个理想非Chetaev 型非完整约束


时间尺度上的Lagrange 函数为

时间尺度上的Hamilton 原理为

并且满足互易条件和边界条件

ui为微粒相对于质点的相对速度.
原理(5)可表示为
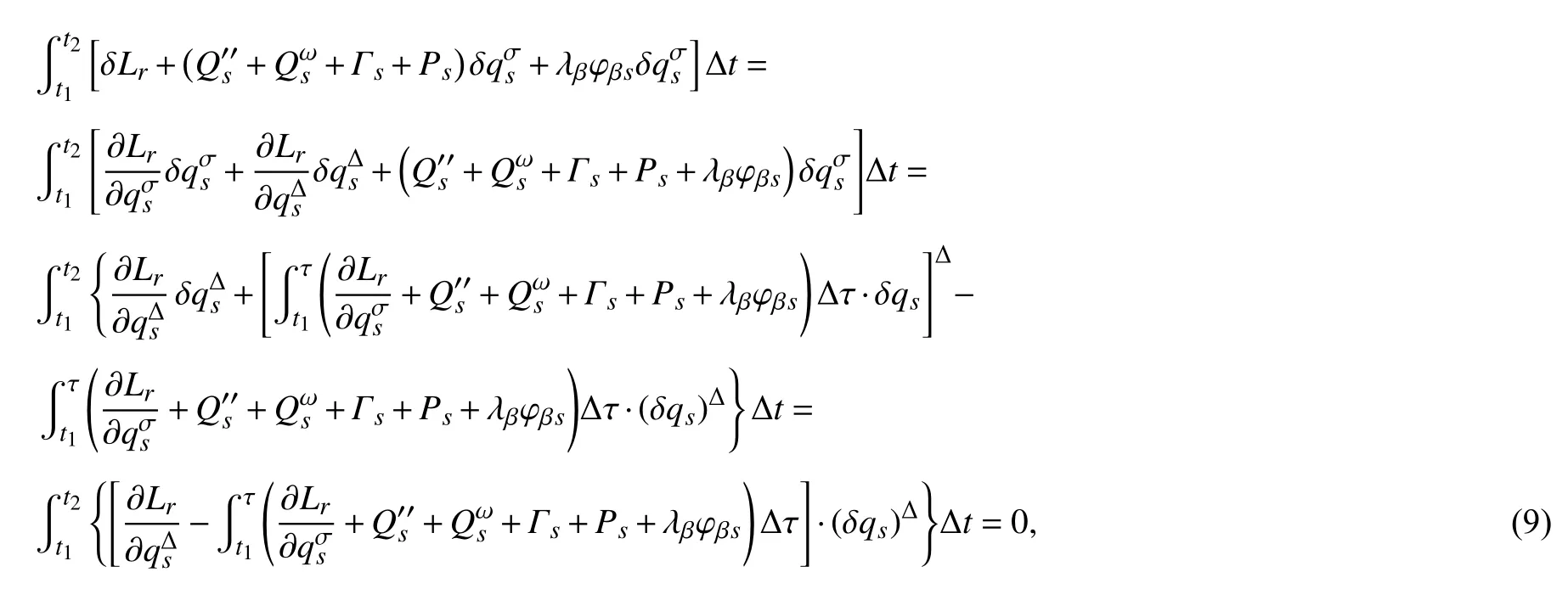
其中 λβ为约束乘子.
根据Dubois-Reymond 引理和(9)式,则可得
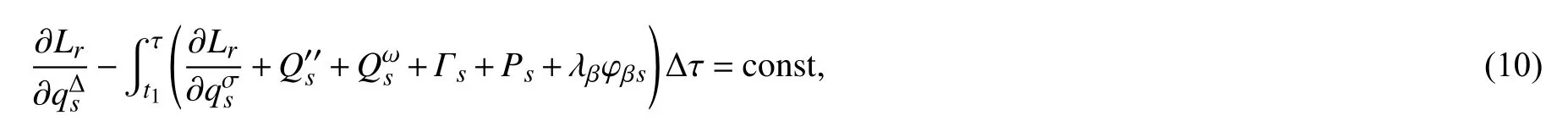
对(10)两边进行求导,可得

令

则方程(11)可表为

方程(13)称为时间尺度上变质量非完整系统相对于非惯性系的运动方程.
假设系统非奇异,即

则由方程(3)和(11)可解得 λβ的函数,进一步可解出所有的广义加速度

2 时间尺度上变质量非完整系统相对于非惯性系的Noether 对称性与守恒量
时间尺度上Hamilton 作用量为

引入无限小变换

其中 ε 为无限小参数,ξ0和 ξs为生成元.
定义1如果在无限小变换(17)下作用量(16)为广义准对称不变量,即对于任意的 [ta,tb]⊆[t1,t2],有(18)式始终成立
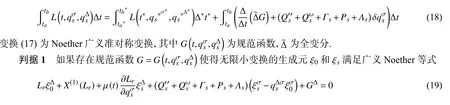
和限制条件

其中

则相应的不变性称为时间尺度上变质量非完整系统相对于非惯性系的Noether 广义准对称性.
定理1如果无限小变换的生成元 ξ0和 ξs满足(19)和(20)式,则时间尺度上变质量非完整系统相对于非惯性系的守恒量为
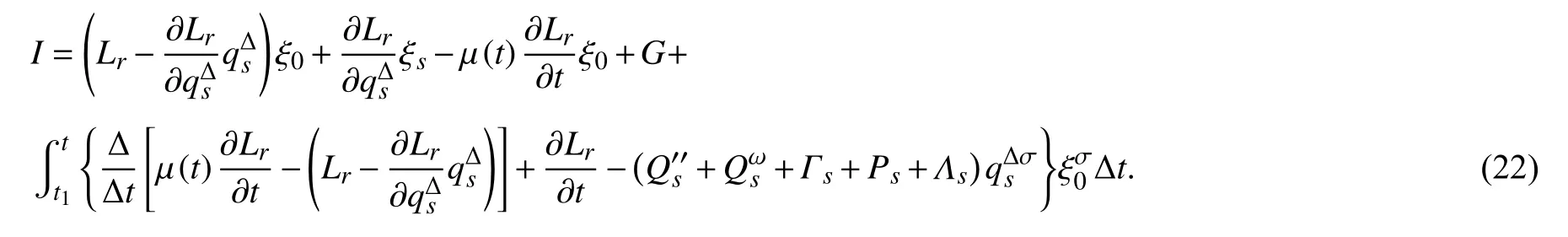
证明:

定理1 得证.
推论1若时间尺度为 T=R,则此时 σ(t)=t,µ(t)=0,进而可推得经典变质量非完整系统相对于非惯性系的Noether 等式
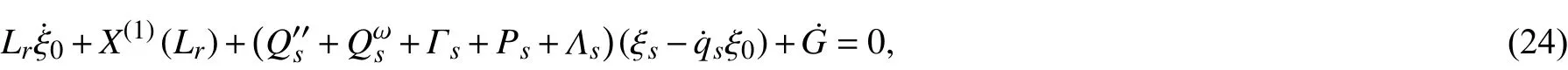
相应的经典变质量非完整系统相对于非惯性系的守恒量[23]为

3 算例
设时间尺度为

时间尺度上的Lagrange 函数为
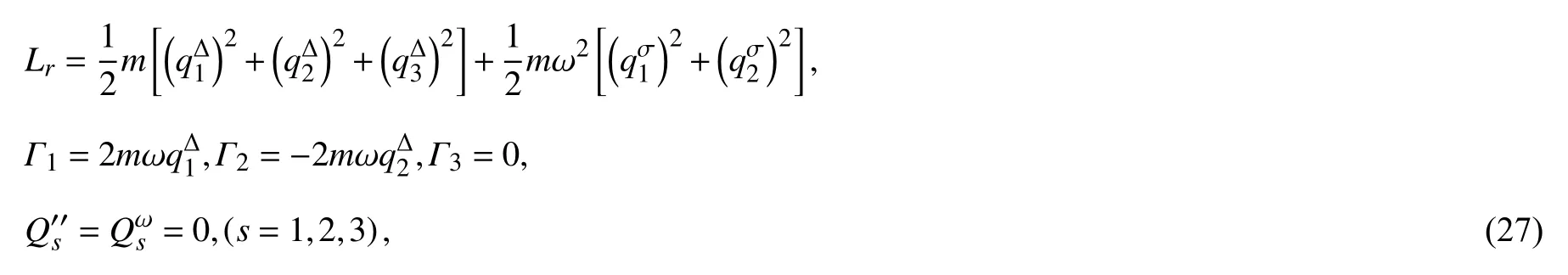
其中m=m0(1−αt),m0、α、ω 均为常数,微粒的绝对速度为0,即

所受的非Chetaev 型非完整约束为

虚位移的限制方程为

试研究系统的对称性与守恒量.
由题可知

由(13)式可得

由(29)、(32)式可解出
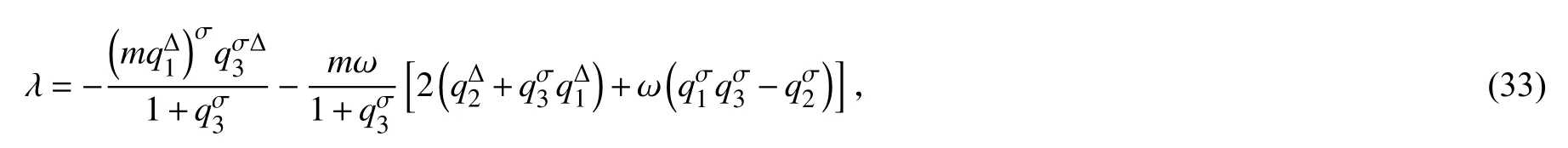
进而可得

则由(18)式可得到

联立方程(35)和(36)可得如下解

根据定理1 可得此系统的守恒量为

4 结论
本文基于时间尺度上的Hamilton 原理,研究时间尺度上变质量非完整系统相对于非惯性系的Noether 对称性和守恒量,主要建立其运动方程,进而给出其Noether 广义准对称性的判据以及守恒量及其证明.文章研究方法可运用到时间尺度上变质量系统相对于非惯性系的Mei 对称性等研究中.

