二元相依生存数据的贝叶斯统计诊断

佘思琪，唐安民

(云南大学 数学与统计学院，云南 昆明 650500)

在生存分析中，同一个个体（比如病人或设备）可能会有2 种类型的事件发生，即我们可以同时观测到同一个体的2 个事件时间.在很多研究中假设个体的这2 个生存过程彼此独立，则可以使用Kaplan-Meier乘积限估计方法[1]估计这2 个生存函数.而实际情况中，这2 个生存过程往往不是独立的，比如一个人2个不同器官的衰竭时间、癌症复发时间和死亡的时间、第一次和第二次感染的时间等.忽略这种相依关系，而作为2 个独立的生存过程来研究，得到的结果往往会是有偏的，甚至是错误的[2].

为了解决这个问题，在相依二元生存分析的研究中，较为流行的方法是Oakes[3]在1989 年提出的脆弱模型（frailty model），在给定脆弱性变量下，各个边际生存时间条件独立，从而实现对生存数据相关性建模.自从Sklar 提出Sklar 定理[4]后，Copula 函数受到了广泛的关注，Copula 函数具有相对简单的形式，可以基于各种参数或非参数模型的边际分布建立依赖结构，Hougaard[5]、Gustafson 等[6]、Romeo 等[7]、Muhammed[8]、Almetwally 等[9]都分别将Copula 函数应用到二元相依生存分析研究中.然而，在二元相依生存数据模型统计诊断方面的国内外研究仍然相对较少，尽管Cho 等[10]、Suzuki 等[11]和Lynch 等[12]均基于Kullback-Leibler 散度(K-L 散度)提出了相依二元生存数据的统计诊断方法，但边缘分布都是基于全参数模型，全参数模型的假定可能偏离实际，导致有偏且不稳健的参数估计.

本研究主要考虑使用FGM Copula 函数[13]度量二元生存过程之间的相依性，B 样条拟合边际对数基本危险函数，从而实现二元相依生存分析的半参数建模.在贝叶斯理论框架下，基于Gibbs 抽样和MH（Metropolis-Hastings）抽样的混合算法，对所拟合的二元生存模型进行参数估计，并提出统计诊断方法，包括数据删除影响分析和局部影响分析.

1 基于FGM Copula 的相依二元生存半参数模型

本节主要在贝叶斯理论框架下，假定事件的生存时间和删失时间相互独立的条件下，对具有相依关系的二元生存数据建立基于FGM Copula 的相依二元生存半参数模型.

1.1 模型建立根据Sklar 定理，一个Copula 函数将能够将不同边际分布连接起来，构造成一个多元联合分布函数，Copula 的参数则描述了变量之间的相关性.设二元联合分布函数H(x,y) 的边际分布为F(x) 和G(y)，则存在一个Copula 函数C，对任意的x,y∈[−∞,+∞]，有

如果F(x) 和G(y) 连续，则C是唯一的，并且该式很容易扩展到多元情况：H(x1,x2,···,xk)=C(F1(x1),F2(x2),···,Fk(xk)).

在二元分析中，对于任意的u,v∈[0,1]，参数为 φ 的Copula 分布函数表示为C(u,v|φ)，对应的密度函数为c(u,v|φ)=条件分布函数分别表示为：常用的Copula 函数有Gauss Copula，Clayton Copula，Frank Copula，Gumbel Copula，FGM Copula 等，不同的Copula 刻画了不同的相关关系，根据Nelson[14]对Copula 的定义，将这些常用Copula 函数的形式和参数取值范围列举如表1 所示.

表1 常用Copula 函数形式和参数取值范围Tab.1 Common Copula function and parameter range

由于FGM Copula 具有简单的结构形式，有利于减轻计算负担，其参数取值范围为[−1,1]，可以同时度量生存过程之间的正相依性和负相依性，因而本文考虑使用FGM Copula建立二元生存时间之间的相关关系.

考虑n个独立个体，令和Ci j分别是第i个个体在第j个生存过程的真实时间和删失时间，其中i=1,2,···,n，j=1,2，本文考虑右删失情形，即只能观测到事件时间并引入示性指标当 δij=1 时，观测到真实生存时间，当 δij=0 时，观测到删失时间，而不是真实生存时间，但知道真实生存时间大于删失时间.令Sij(tij) 和fij(tij) 分别表示第i个个体在第j个生存过程中在tij的边际生存函数和边际密度函数，则基于FGM Copula，可得 (Ti1,Ti2) 的联合生存函数和联合密度函数如下：

其中，参数 φ 衡量了生存时间之间相依性的强度，并且当 φ=0 时，Ti1和Ti2独立，即有Si(ti1,ti2|φ)=Si1(ti1)Si2(ti2).

接下来，基于边际危险函数 λi j(ti j) 对包含在（2）式中的边际生存函数Sij(tij) 和边际密度函数fij(ti j) 建模.通常地，边际危险函数 λi j(ti j) 可以建模如下：

其中 βj是协变量Xi=(xi1,···,xip)T系数向量，非负函数 λ0j(ti j) 表示第j个生存过程中不考虑个体差异的基本危险函数，则边际生存函数为：

由(3)，(4)式易得第i个个体的第j个边际密度函数为fij(tij)=Sij(tij)λij(tij).在(4)式中未知的基本危险函数 λ0j(ti j)，用B 样条[15]建模其对数基本危险函数如下：

这里的k=1,2,···,qj+Kj+1.

由于(4)式涉及到复杂的积分运算，本文基于矩形近似积分方法提出一种高效计算方法[17]，将第j个生存过程中的事件时间轴用Lj+1 个时刻分为首尾相连但不相交的Lj个小区间：(c0j,c1j],(c1j,c2j],···,并且有c0j=0，则结合(4)，(5)式，边际生存函数Sij(tij)可以表示如下：

显然，当tij＜cl−1,j，Iijl=0，该方法可以高效计算第i个个体的第j个生存过程的边际生存函数和边际密度函数

令Di=表示第i个个体观测到的事件时间和删失指标，D=(D1,···,Dn)，在假定事件的生存时间和删失时间相互独立及个体间相互独立的条件下，得到参数的联合似然函数为：

其中第i个个体的似然函数Li(Di|φ,β1,β2,φ1,φ2) 可以表示如下：

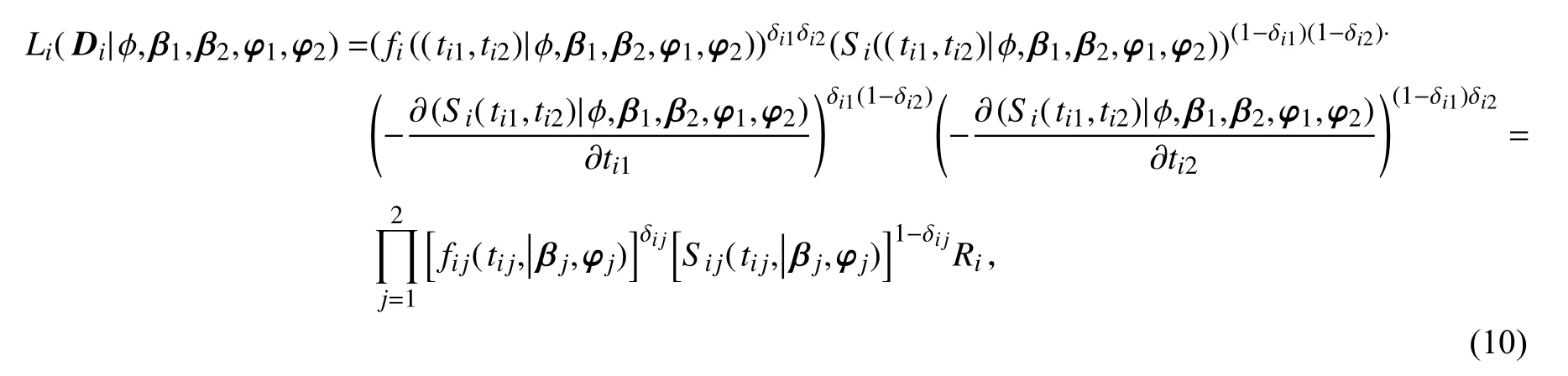
其中Ri表示与参数 φ 有关的项，具体表示如下：

其中 θ[−φ]表示 θ 中除了参数 φ 以外的参数集合，表示类似，显然各个参数的条件后验不是常见的概率分布形式，不能直接从常见的分布形式中得到，本文借助Gibbs 抽样和MH 抽样的混合算法，对各个参数（向量）进行估计，步骤如下：

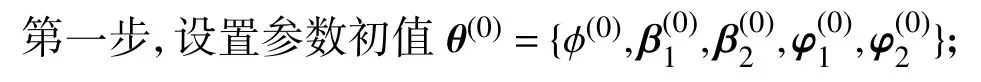
第二步，对于第s(s=1,···,S) 步迭代，各个参数值迭代更新如下：

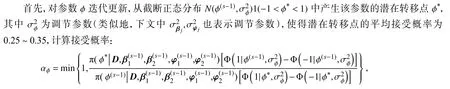
并从均匀分布U(0,1)中产生随机数uφ，如果uφ≤αφ，则取φ(s)=φ*，否则φ(s)=φ(s−1).

第三步，不断迭代第二步，直到产生的马尔科夫链依分布收敛到目标分布.

2 统计诊断

统计诊断是数据分析中的重要组成部分，本节在贝叶斯框架下，提出一种适合二元相依生存模型的数据删除影响分析和局部影响分析方法，检测出数据中影响模型的潜在异常点或强影响点.

2.1 贝叶斯数据删除影响分析在贝叶斯分析中，基于数据删除的K-L 距离是对有特定数据点和没有特定数据点的后验分布之间差异的度量.π(θ|D) 表示给定所有个体数据下 θ 的条件后验概率密度，π(θ|D[−i])表示删除第i个个体数据后 θ 的条件后验概率密度，基于K-L 距离考虑如下贝叶斯诊断测度：

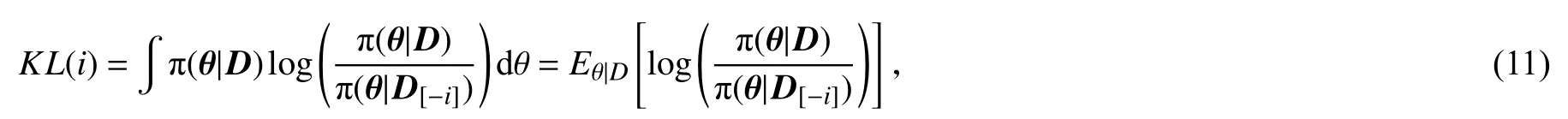
该值度量了条件后验概率 π(θ|D) 和 π(θ|D[−i]) 的距离，较大的KL(i) 值意味着删除第i个个体的数据可能对参数 θ 后验概率的计算产生较大影响.(11)式需要计算 π(θ|D[−i]) 的值，如果每删除一个个体就计算一次删除该个体数据后 θ 的条件后验概率密度，计算量将不堪重负，还好，在个体间相互独立假定下，可以证明 π(θ|D) 和 π(θ|D[−i]) 有如下关系：

其中Li(θ) 表示第i个个体的似然函数值，因此(11)式可以变换为：(11)式在求期望时涉及到难以精确计算的积分，因此采用蒙特卡洛积分可近似如下：

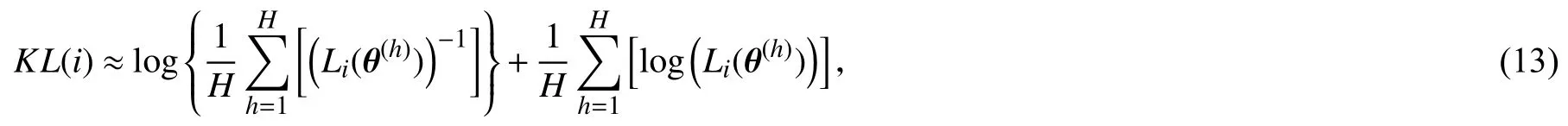
其中 θ(h) 表示从 π(θ|D) 抽取的第h次观测值.

2.2 贝叶斯局部影响分析局部影响有助于识别数据对模型中的微小影响[18]，在生存数据的贝叶斯分析中，局部影响分析被发展为一类敏感性分析方法，基于Zhu 等[19]的局部影响方法，本文发展了二元相依生存模型的贝叶斯局部影响诊断方法.令 ω=(ω1,···,ωW) 表示扰动向量，表示扰动后的模型，刻画了对原假定模型 M={p(D,θ)} 的不同扰动，满足合适的扰动模型中，总存在扰动向量使得即这一扰动向量对模型没有扰动.在贝叶斯框架下，扰动模型主要靠W×W维Fisher 信息矩阵来刻画，记作和 ωk分别为 ω 的第w个分量和第k个分量，令则有：

其中Eω表示对p(D,θ|ω) 求期望，gww(ω) 可以解释为扰动 ωw的扰动程度，gwk(ω) 表示 ωw和 ωk的关联，因此刻画了扰动分量 ωw和 ωk的相关程度，值越接近于1，认为 ωw和 ωk在扰动模型中作用越相似.合适的扰动模型总要求 G(ω0) 是对角矩阵，当 G(ω0) 不是对角矩阵时，我们总能选择一个新的扰动向量=ω0+G(ω0)12(ω−ω0)，并且

考虑对 ω 和 ω0的贝叶斯因子取对数，有：B(ω)=ℓ(ω)−ℓ(ω0)，令 ω(t) 表示扰动模型 M={p(D,θ|ω)},ω ∈RW的扰动向量，取 ω(t)=ω0+th，并且 ω(0) 表示无扰动，得到一阶Taylor 展开式：B(ω(t))=B(ω(0))+其中在沿着h的方向上定义一阶局部影响测度为：

其中 FIB,h的最大值等价于的最大特征值，记作hmax，该值量化了扰动模型中 ω 局部影响的最大程度，并与最大特征值的特征向量相对应，揭示了如何扰动模型从而得到贝叶斯因子的最大局部改变，进而识别出潜在的影响观测.在某些平滑条件下，可以得到：

其中为 G(ω0) 表示在 ω0处的Fisher 矩阵.计算关于B(ω) 的局部影响度量，我们仅需要计算 ∇B和 G(ω0)，可以用蒙特卡洛方法近似.在我们所提出的相依二元生存模型中，根据Ibrahim 等[20]的建议，考虑对第w个个体观测值的生存过程进行如下的扰动：

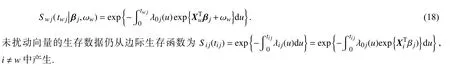
3 数值模拟与实例分析

本节基于数值模拟和实例数据分析，验证我们建议模型的可行性和统计诊断方法能否以较大概率找出潜在的异常点或强影响点.

3.1 数值模拟产生300 个生存数据的样本，其中FGM Copula 中相关系数 φ=0.8，2 个边际分布的基本危险函数假定如下：1+0.5cos(1.5πt) 和 1+0.7cos(2.5πt).为了模型可识别，不考虑截距项，分别从参数为0.5的二项分布和2 个标准正态分布独立产生3 个协变量xi1,xi2,xi3，i=1,···,300，未知参数向量 β1=(1.5,1,1)T和 β2=(2,−1,1)T，如此设置使得删失率在20%～25%，样条次数设置为2 并取5 个内部节点.进行积分近似运算时，划分100 个小积分区间.为了检验马尔科夫链的收敛性，从不同的初值出发产生3 条平行的马尔科夫链，每条链迭代10 000 次，通过计算感兴趣参数（φ,βj,j=1,2）的EPSR（Estimated Potential Scale Reduction）值的方法[21]来判断生成的链是否收敛，如果迭代大于5 000 次时所有参数的EPSR 值都小于1.2，则认为5 000 次以后的马尔科夫链已经收敛了.为了判断基于B 样条建模的基本生存函数是否收敛，在其定义域中均匀插入20 个点，以这20 个点拟合的基本生存函数拟合值作为“虚拟参数”值，计算这些“虚拟参数”的EPSR 值，与感兴趣参数的EPSR 值一起作图，得到图1.

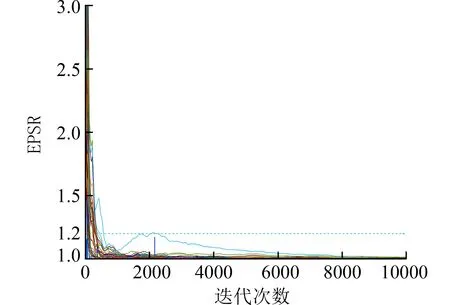
图1 数值模拟中参数EPSR 值Fig.1 EPSR values of parameters in simulation

当迭代次数为5 000 时，所有参数的EPSR 值都小于1.2，因此本文进行100 次重复试验，每次试验中丢掉前5 000 次迭代值，为避免自相关，使用后5 000 次间距为2 的迭代值的平均值作为未知参数 θ 在第v次重复试验的贝叶斯估计值最终得到各参数的贝叶斯估计值：均方根误差：RMS=以及参数偏差：Bias=汇总得到表2.计算基本生存函数的均方根误差：RASE=并在图2 中画出RASE中位数对应那次试验的基本生存函数拟合图.

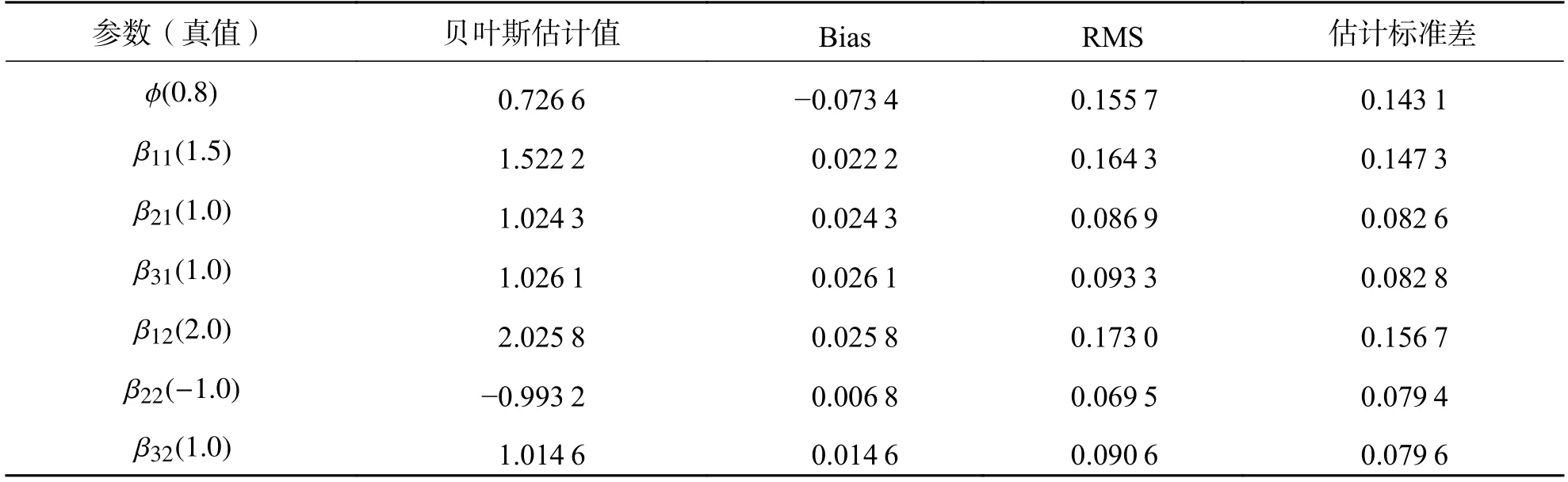
表2 FGM Copula 半参数二元生存模型的参数估计Tab.2 Parameters estimation of FGM Copula semiparametric bivariate survival model

根据表2 和图2，各个感兴趣参数的偏差的绝对值均小于0.1，均方误差根RMS 小于0.2，估计标准差也均小于0.2，可认为参数估计较为精确和稳健，边际基本生存函数的拟合曲线与真实曲线很接近，除尾部有轻微偏差外，总体拟合的效果较好.

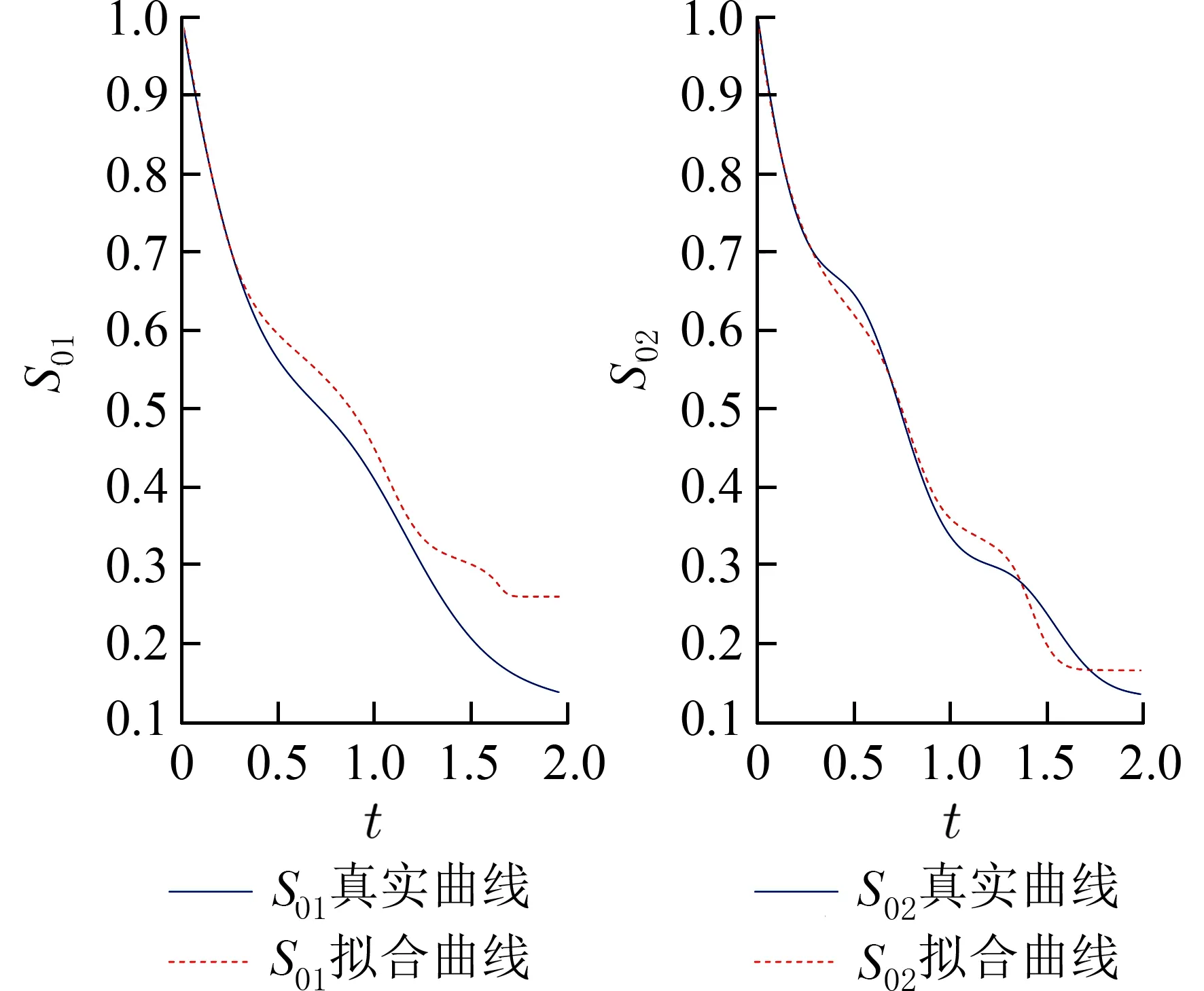
图2 数值模拟中边际基本生存函数拟合图Fig.2 Fitting plot of marginal baseline survival functions in simulation

接下来，基于贝叶斯数据删除影响分析和贝叶斯局部影响分析诊断二元相依生存数据是否存在异常点.首先，数据产生同前，人为产生异常点或强影响点如下基于(13)式计算K-L 贝叶斯诊断统计量，作图得到图3，说明我们建议的数据删除影响分析方法能诊断出潜在的异常点.其次，为验证本文所提出的局部影响诊断方法，产生新的生存时间 {ti j|i=80,150,200,j=1,2} 作为异常点或强影响点，方法如下：t80j和t150j分别从边际危险函数为

图3 数值模拟中贝叶斯数据删除影响诊断图Fig.3 Diagnostic plot of Bayesian data deletion influence analysis in simulation

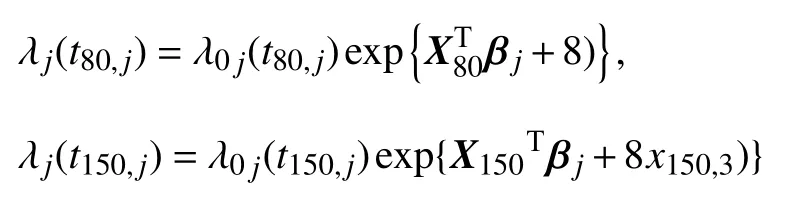
的生存分布中产生，t200,1和t200,2则从边际危险函数是

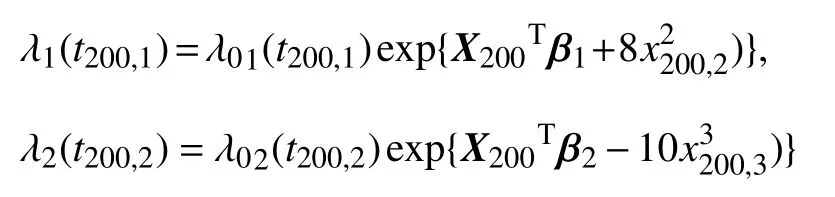
的生存分布中产生，其余数据产生方法同前，然后基于(17)式计算 |hmax|.类似于Zhu 等[22]，选取作一基准线（m通常取2），表示向量的均值和标准差，结果如图4 所示，不难看出所有的潜在影响点都被正确诊断出来，说明本文所提出的统计诊断方法有良好的性能.

图4 数值模拟中贝叶斯局部影响诊断图Fig.4 Diagnostic plot of Bayesian local influence analysis in simulation

3.2 实例分析糖尿病视网膜病变是与糖尿病相关的并发症，糖尿病视网膜病变研究(DRS)始于1971 年，目的是研究激光光凝治疗在延缓糖尿病视网膜病变患者失明的有效性[23].每个患者的一只眼睛随机选择治疗，另一只眼睛不治疗，本文使用DRS 标准定义的高危患者样本为分析子集(n=197)对所提出的模型进行研究.对于该样本数据，观测得到的事件时间是患者失明时间或随访结束等原因造成的删失时间，当获得的是失明时间时，标记为1，否则获得删失时间，标记为0.以患者年龄作为协变量，生存过程1 用来建模接受治疗眼睛的生存数据，生存过程2 用来建模未接受治疗眼睛的生存数据，用本文所提出的半参数二元相依生存模型对数据进行拟合.设置样条次数为2 并取1 个内部节点，先计算各个感兴趣参数和虚拟参数的EPSR 值，绘制图5.显然当迭代次数为5 000 时，所有参数的EPSR 值都小于1.2，因此燃烧前5 000 次，并且为避免自相关，取后5 000 次间距为2 的迭代样本的均值作为参数估计值，得到参数估计值见表3.

图5 实例数据分析的EPSR 图Fig.5 EPSR values of parameters in real data analysis

表3 实例数据分析的参数估计Tab.3 Parameters estimation of real data analysis

根据表3，Copula 相关参数φ估计值为0.821 1，且在显著性水平为0.05 时，95%的可信区间不包括0，因而我们认为接受治疗眼睛的生存数据和未接受治疗眼睛的生存数据2 者存在显著正相关关系.另外，β11=−0.018 8 表明在控制其他条件不变的情况下，接受激光光凝治疗的患者随着年龄的上升，失明的时间变短，即治疗效果变差，同时得到2 个生存过程的基本生存函数的拟合图，见图6 所示.

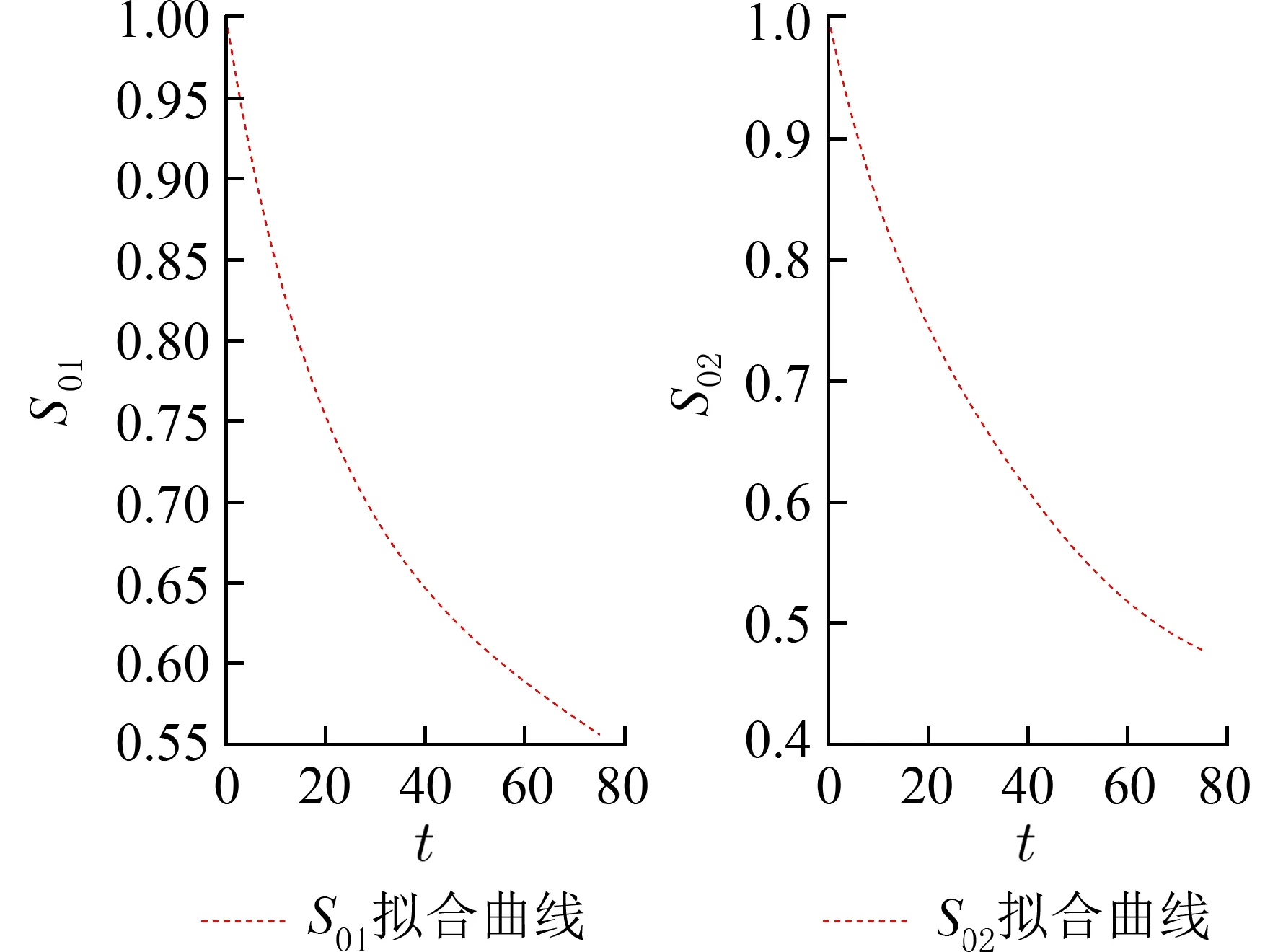
图6 实例数据的边际基本生存函数模型拟合图Fig.6 Fitting plot of marginal baseline survival function in real data analysis

为了进一步说明所提出模型对实例数据的拟合效果，本文用DIC 信息准则（Deviance Information Criterion）对所提出的二元相依生存半参数模型与二元独立半参数生存模型（φ=0）、边际生存分布为Weibull 分布的二元相依全参数生存模型和二元独立全参数生存模型进行比较，整理得到表4.

根据表4，显然无论是否考虑生存过程的相依性，半参数生存模型的DIC 值均比全参数模型的DIC 值小，说明半参数模型对数据进行生存分析要比全参数模型更好；同时，相依模型的拟合效果也优于独立模型，因而也侧面说明了在对二元生存过程建模时不应该忽略生存过程之间的相依性问题.另外，本文所提出的相依性半参数模型的DIC 值为3 370.402 9，比其他3 个模型都要低，说明该模型在这个实例数据中具有良好的表现，即本文所提出的模型具有较好的实用意义.

表4 实例数据分析模型比较Tab.4 Model Comparison in real data analysis

最后本文对实例数据进行贝叶斯数据删除影响分析和贝叶斯局部影响分析，得到图7 和图8，在数据删除影响分析中第28、102、120、183 个个体被诊断为异常点，在局部影响分析中第28 和49 个个体被诊断为影响点，第23、32、111、120、122 个个体也对模型有一定的扰动影响.

图7 实例数据的贝叶斯数据删除影响诊断图Fig.7 Diagnostic plot of Bayesian data deletion influence analysis in real data

图8 实例数据的贝叶斯局部影响诊断图Fig.8 Diagnostic plot of Bayesian local influence analysis in real data

4 总结与展望

本文主要通过引入FGM Copula 函数将个体的不同边际生存过程联系起来，基于B 样条函数建立二元相依生存分析半参数模型，在贝叶斯理论框架下，对所提出的相依二元生存分析模型进行贝叶斯数据删除影响分析和贝叶斯局部影响分析的统计诊断，最后，将所建议模型应用到糖尿病视网膜病变研究实例数据中，验证了模型的可行性.

在本文的研究基础上，下一步研究方向可以有以下方面：首先将相依二元生存分析通过Pair-Copula理论或者多元FGM Copula 进一步拓展到多元的情形，但是随着生存过程的增加，模型的复杂度也会进一步增加，给参数估计造成困难；其次，本文仅考虑了右删失的情况，为了更具普遍性，可以拓展到区间删失、截尾数据，甚至是考虑缺失数据的情况.