毒素影响下具反馈控制和非线性抑制项影响的一类三种群捕食−竞争离散时滞系统的持久性分析
蔡旖旎,刘 萍,李 艳
(云南大学 数学与统计学院,云南 昆明 650500)
我们知道,在生态系统中,对生命短、世代不重叠的种群,或者即使生命长、世代重叠的种群,其数量较少时,通常用差分方程(离散系统)来刻画更为合理.
2019 年,苏倩倩[1]提出了如下的一类离散Leslie-Gower 三维食物链系统
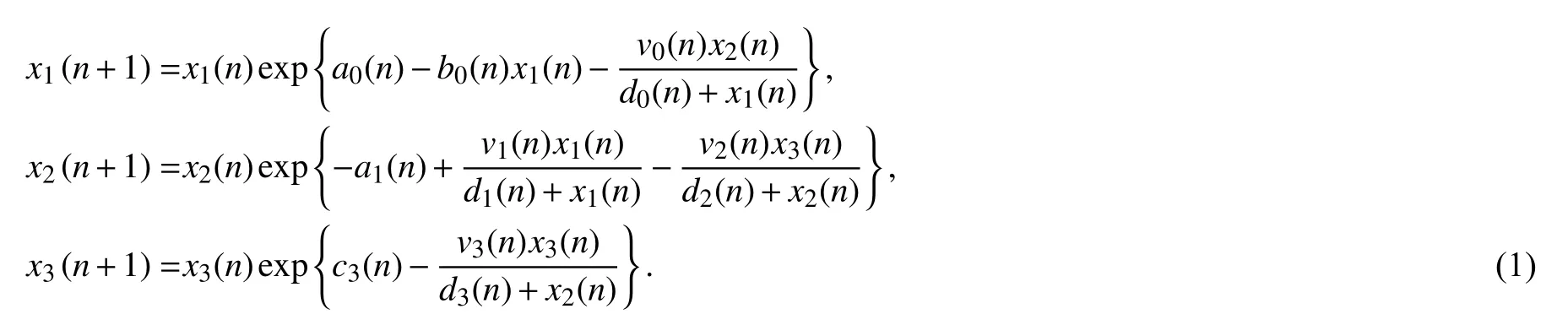
其中,a0,b0,v0,d0,a1,v1,d1,v2,d2,c3,v3,d3均为有正的上下界的序列,运用差分不等式有关结论,得到了种群x1,x3持久,x2灭绝的条件,通过构造Lyapunov 函数,得到系统(1)全局吸引的充分性条件.而在现实环境中,反馈控制变量是不可忽略的影响因素,文献[2]研究了如下具反馈控制和Holling-Ⅲ类功能反应的离散时滞系统

其中,xi(n)(i=1,2) 为种群xi第n代的种群密度,捕食者x2具有Holling-Ⅲ类功能反应,b1(n) 为种群x1的出生率,b2(n) 为种群x2的死亡率,a1(n) 为密度制约系数,αi(n)(i=1,2) 为转换率,m为半饱和度,0 <≤<1(i=1,2),a1(n),bi(n),αi(n),ei(n),ηi(n),di(n)(i=1,2) 为有正的上下界的非负序列,通过运用差分不等式的相关结论和计算技巧,得到了系统(2)持久生存的充分条件.学者们对具有Holling-Ⅲ类功能反应的种群模型进行广泛研究,文献[3]研究了一类具有Holling-Ⅲ类功能反应函数的捕食−食饵反应扩散系统,讨论了系统发自唯一半平凡解处的分歧解的局部和全局存在性.文献[4]研究时标上具有捕获率和投放率的Holling-Ⅲ类功能反应的捕食系统,考虑了时滞效应,得到了系统至少有一个正周期解的结论.更多研究可参考文献[5-6]及相关参考文献.
近年来,诸多学者研究了具有毒素影响的生态系统,发现毒素对系统的动力学行为有影响,如文献[7]中研究了具毒素影响和非线性相互抑制项的离散竞争系统
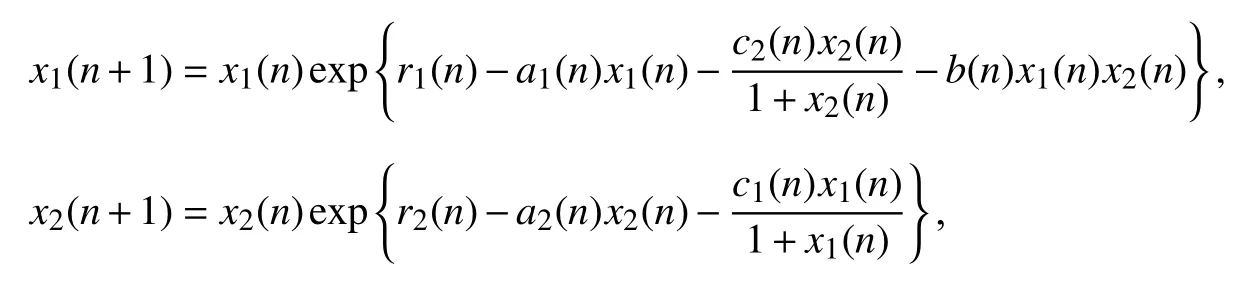
得到了一个种群灭绝而另一个种群全局吸引的充分条件.
基于以上研究基础,考虑到现实生态环境中毒素的影响以及种群间的竞争和捕食关系,作为系统(2)的推广,本文研究毒素作用下具反馈控制和非线性抑制项影响的3 种群捕食−竞争离散系统

其中,xi(n)(i=1,2,3) 为种群xi(n)(i=1,2,3) 第n代的种群密度,x1,x2为食饵种群,x1,x2有竞争关系,x3为捕食者种群,种群x1,x2与x3是捕食关系,且具有Holling-Ⅲ功能反应,r1(n),r2(n) 为种群x1,x2的出生率,r3(n) 为种群x3的死亡率,a1(n),a2(n) 为种群内的密度制约系数,b1(n),b2(n) 为种间竞争系数,为非线性抑制项,c1(n),c2(n),c3(n),c4(n) 为转换率,r(n) 为毒素影响系数,为种群x2释放毒素对第一个种群的影响,k>0 为正数,m1,m2为半饱和度且m1>0,m2>0,时滞τ1,τ2,δ1,δ2,δ3,ξ3,ξ4,η1,η2,η3均为正数,ui(i=1,2,3) 为反馈控制变量,fi(n),gi(n) 为控制变量系数,可通过其变化调节对系统控制的强弱.文中总假设r1(n),r2(n),r3(n),r(n),a1(n),a2(n),b1(n),b2(n),c1(n),c2(n),c3(n),di(n),ei(n),fi(n),gi(n) 均为具有正的上下界的非负序列且系统(3)具有如下初始条件

其中 τ=max{τ1,τ2,δ1,δ2,δ3,ξ3,ξ4,η1,η2,η3}.
对于任意有界序列 {h(n)},记
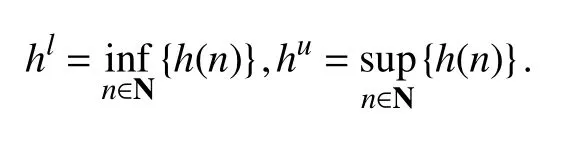
n∈N+xi(n)>0,ui(n)>0,i=1,2,3.
容易知道,系统(3)满足初始条件(4)的解在 时都有
1 预备知识
引理 1[8]假设序列 {x(n)} 满足x(n)>0,a(n) 和b(n) 均是有正的上下界的非负序列,若x(n+1)≤x(n)exp{a(n)−b(n)x(n)},n∈N,则

引理 3[10]假如A>0,y(0)>0 且y(n+1)≤Ay(n)+B(n),n=1,2,···,则

若A<1,B(n) 有上界M,则

引理 5[12]假设A>0,y(0)>0,且y(n+1)≥Ay(n)+B(n),n=1,2,···,则
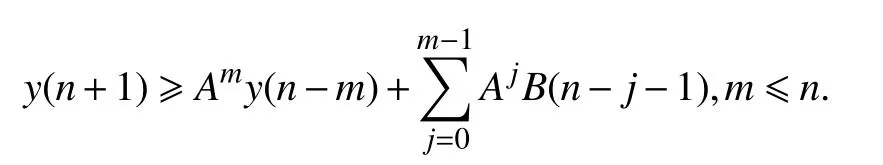
若A<1,B(n) 有上界P,则

2 持久性分析
引理 6假设系统(3)满足条件

则存在正数Li,Ni(i=1,2,3),使得

证明 假设 (x1(n),x2(n),x3(n),u1(n),u2(n),u3(n))T为系统(3)的任意正解,由系统(3)的第一个方程得

因此

即

由式(5),(6)得

由引理1 得

类似地,由系统(3)的第2 个方程得

由系统(3)的第3 个方程及均值不等式得
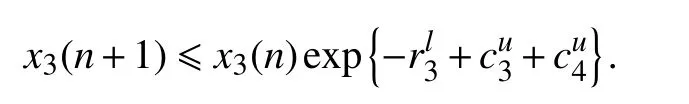
令z(n)=lnx3(n),则

其中

由引理2 得
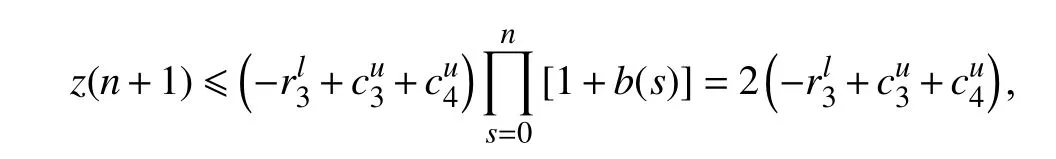
进而

则

对于充分小的正数 ε,存在K1>0,K1∈N,当n>K1时,有

由系统(3)第4 个方程和式(10)得

令 ε →0,由引理3 得
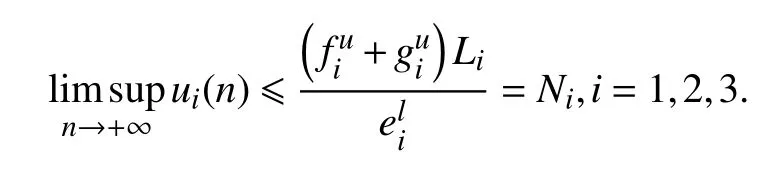
证毕.
定理 1若系统(3)满足条件

则系统(3)是持久的,即存在正数li,hi,Ni,Li(i=1,2,3),使得

其中,Li,Ni如引理6 中所示,li,hi在下面证明中给出定义.
证明由 (H3) 可以得到 (H1) 成立,故在 (H3) 成立时引理6 的结论成立.由引理6 知对 ε>0,存在K2>K1,K2∈N,对于任意的n>K2+τ,都有

由系统(3)的第一个方程和(11)式得
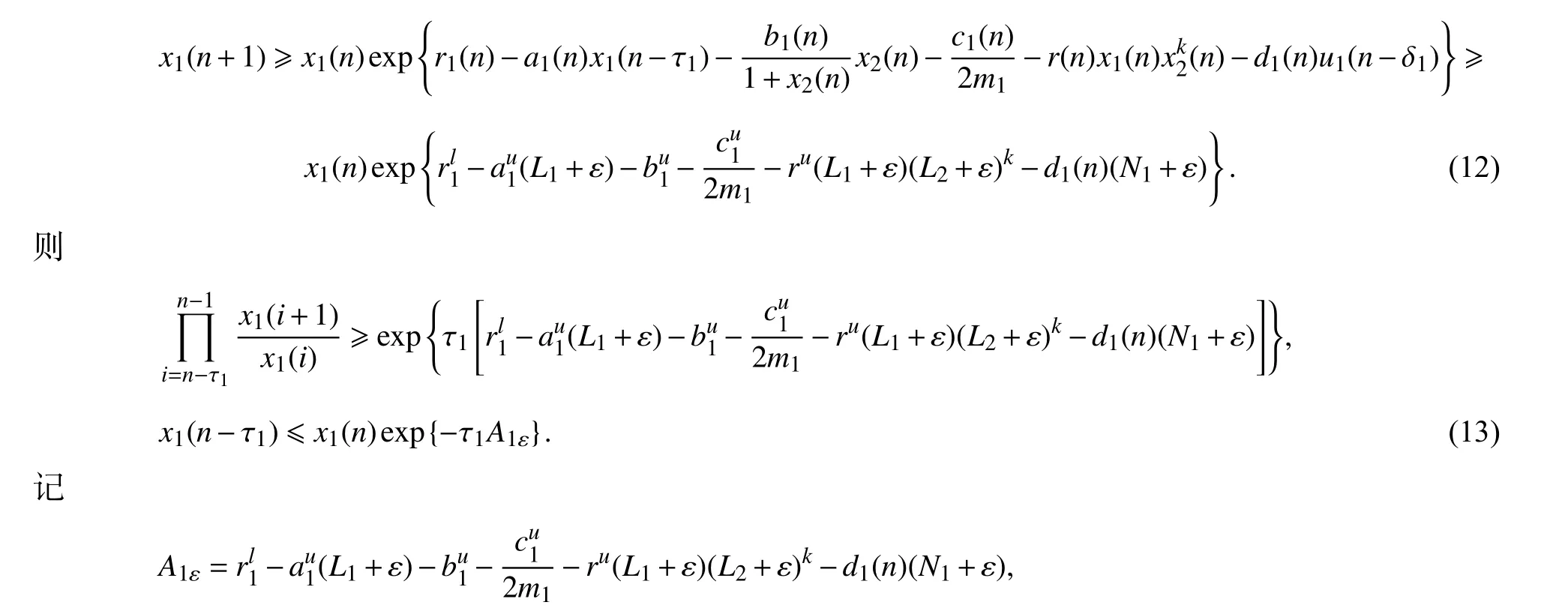
由(12),(13)式得
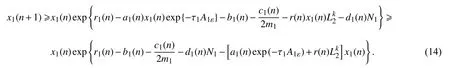
令 ε →0,由引理4 得

类似地,由系统(3)的第2 个方程得

故对任意 ε>0,存在K3>K2,K3∈N,当n>K3+τ,有

由系统(3)的第3 个方程得

令 ε →0 有
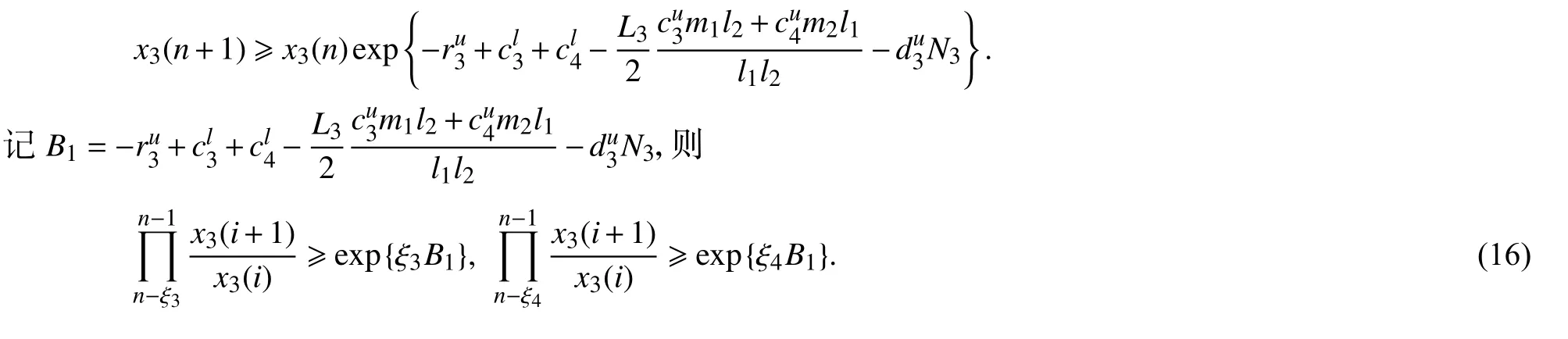
代入(15)式,得

记

则
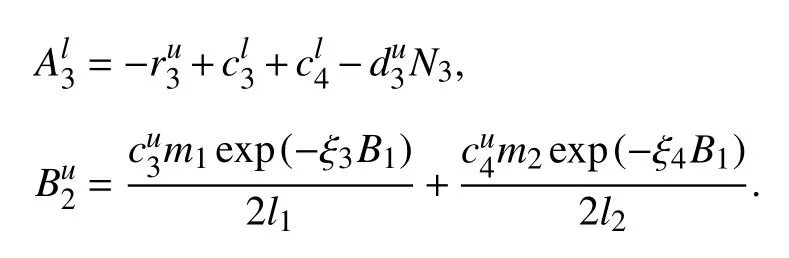
由引理4 得

由(17)式,对于任意 ε>0,存在K4>K3,K4∈N,当n>K4时,有

由系统(3)的第4 个方程得

令 ε →0 得

由引理5 得

证毕.
3 实例
下面举例说明我们理论结果的可行性.
例 1考虑如下系统
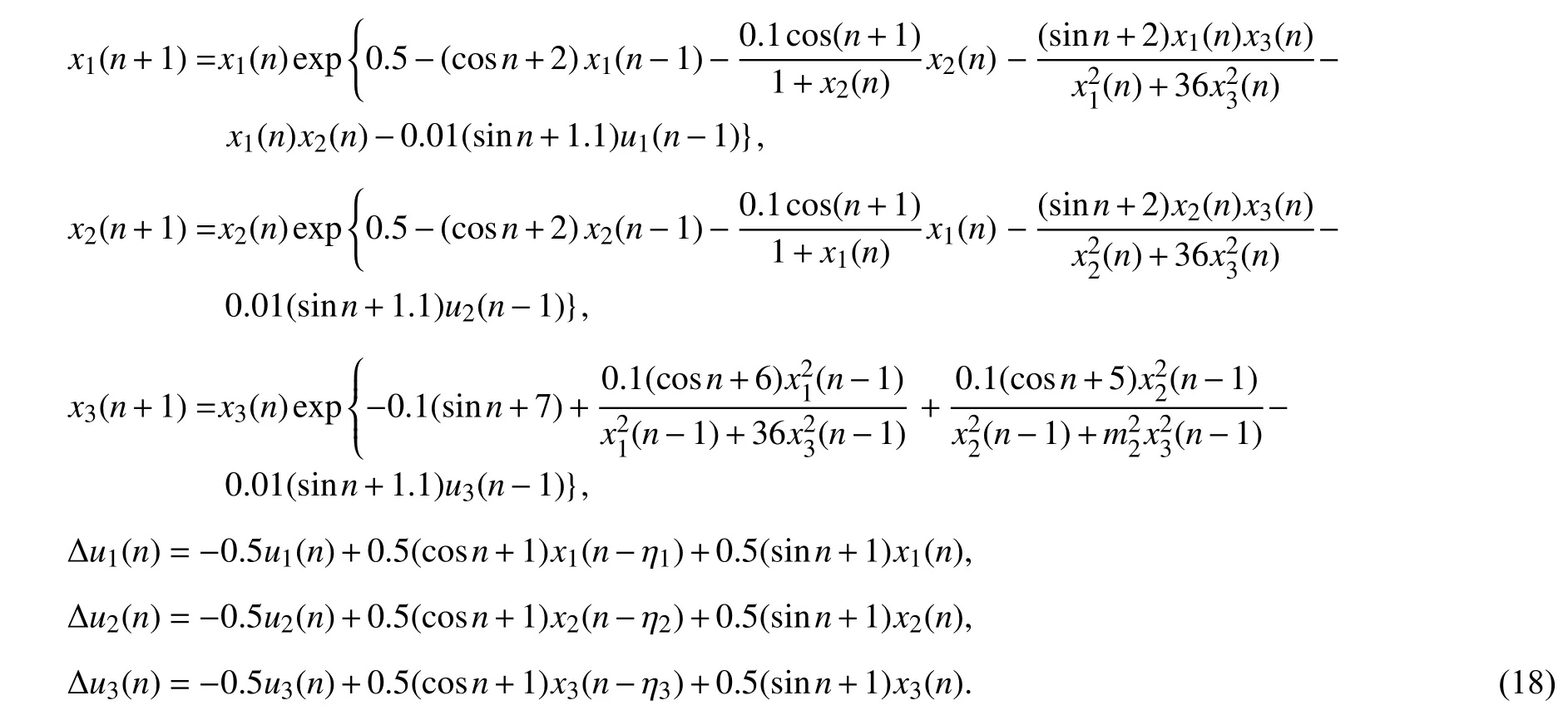
对系统(18),假设

经过计算,得
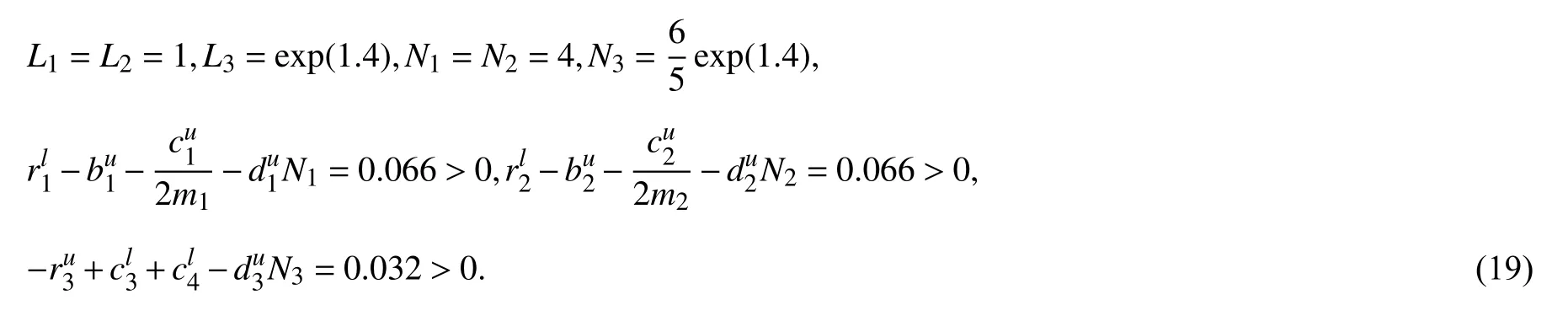
满足定理1 条件,因而种群x1,x2,x3持久生存.
4 结论
本文提出一类毒素影响下具有时滞、反馈控制和非线性抑制项的离散三种群混合系统,据作者所知,至今尚未有学者研究此类系统,系统是新的.运用差分方程比较原理和相关不等式计算技巧,研究了该系统持久性生存的充分条件,结果显示:当种群x1和种群x2的出生率的下确界足够大时,种群x1和x2可持久生存;当种群x3的死亡率的上确界足够小时,种群x3可持久生存.本文研究结果推广了文献[2]的相关研究结果.本文研究结果表明,时滞、反馈控制和毒素均会影响目标系统的持久性.

