逐级删失定时截尾恒加寿命试验模型的抽样方案设计

杨春燕，胡 品

(云南大学 数学与统计学院，云南 昆明 650500)

为判断一批产品是否合格，我们通常使用抽样检验的方法，即从该批产品中随机抽取少量产品（样本）进行检验，据此判断该批产品是否合格.对于合格的产品批选择接收，不合格的拒绝.这就涉及到抽样方案的制定，具体来说就是需要确定抽取的样本量以及接收和拒绝的准则.如果检验的质量指标是产品的寿命，那么这样的抽样检验就被称为可靠性抽样检验.当全部样本的寿命都可以观测到时，我们可以使用标准的可靠性抽样方案（如MIL-STD-414 和MIL-STD-105）判断该批产品是否能够被接收.然而，在很多实际应用中，由于时间和费用的限制，我们不能够观测到所有样品的寿命，特别是对于那些高可靠长寿命的产品.因此，定时或定数截尾模型通常被使用.

在实际应用中，定时截尾和定数截尾通常分阶段发生，并且在每一阶段可能会有未失效的产品被随机移走，这被称为带有随机移走的逐级删失模型.这一模型首先于1996 年在文献[1]中被提出，之后受到广泛关注，详细的讨论可见文献[2].特别地，文献[3-5]分别假定产品寿命服从双参数指数分布、Weibull 分布以及对数正态分布，研究了普通寿命试验在定数截尾逐级删失模型下的可靠性抽样方案设计（每个阶段被移走的产品数目是事先确定的）.文献[6]假定产品寿命服从Weibull 分布，研究了普通寿命试验在带有随机移走的定数截尾模型下的可靠性抽样方案设计（每个阶段被移走的产品数目是随机的）.随着科学技术的进步，高可靠长寿命的产品越来越多，使用普通截尾寿命试验仍然很难在有限的时间内观测到样品的失效，因此，加速寿命试验被广泛使用，其中恒加寿命试验因其实际操作简单而备受实验者的青睐.文献[7]和[8]分别研究了产品寿命服从指数分布和对数正态分布时，带有随机移走的逐级删失定时截尾恒加寿命试验的优化问题.此外，文献[9]研究了简单步加寿命试验在定时截尾逐级删失模型下的优化设计.然而，恒加寿命试验在带有随机移走的逐级删失截尾模型下的抽样方案设计至今尚未见报道.

本文中，假定产品寿命服从对数正态分布，研究了带有随机移走的逐级删失定时截尾恒加寿命试验模型的抽样设计.假定被随机移走的受试产品数服从二项分布，考虑了高于正常状态的2 个应力水平，并假定对数寿命分布的固定参数与应力水平是线性关系.我们通过极小化广义渐近方差得到低应力水平的最优值以及样品在个应力水平下的最优分配比例，再通过操作特征曲线（Operating Characteristic curve，简称OC 曲线）确定接收系数和所需的样本量.

1 模型的建立

假定产品的寿命X服从参数为 µ 和 σ 的对数正态分布，其密度函数f(x,µ,σ) 可以写为f(x,µ,σ)=则Y=ln(X) 服从正态分布N(µ,σ2)，且其分布函数F(y)可表示为F(y)=为方便计算，通常我们用来进行代换.假定 µ与应力水平s有如下关系：µ=β0+β1s.这里s可取s0，s1和s23 个水平，分别代表正常水平、低应力水平和高应力水平，s0＜s1＜s2.

假定试验的总样本量为n，分配到应力水平si下的样本量为ni，i=1,2.则各应力水平下的样本量可表示为：n1=α1n，n2=(1−α1)n，α1为分配系数，0 ＜α1＜1.试验采用间隔观测，tij表示第i个应力水平下第j个观测点的时间（i=1,2;j=1,2,···,ki），我们在试验前给出其确定值.在试验中我们需要记录下2 个观测点(ti,j−1,ti j) 之间的失效产品数ni j.不失一般性，令ti0=0，=∞.另外，假设rij为第i个应力水平下第j个观测点被随机移走的未失效产品数目，并且rij是服从参数为p的二项分布.在试验结束的时间剩余的未失效产品数记为这样，通过试验中观测到的数据 {nij,rij,i=1,2;j=1,2,···,ki}，我们可以用极大似然估计的方法分别求得 β0和 β1的估计值和，并通过尺度参数 µ 与应力水平s之间的关系，推断在正常水平下我们关心的寿命分布的参数.

试验者通常关心的是寿命均值 µ 的估计或在正常应力水平下的q分位数tq.如果产品的寿命服从对数正态分布，则q分位数为：yq=lntq=µ0+σzq，其中 µ0=β0+β1s0，zq为标准正态分布的q分位数.相应的极大似然估计分别记为：

我们通过给定的参数可以确定出最优的s1和 α1，使得的方差（或渐近方差）达到最小.另一方面，我们关心的是在该模型下的抽样方案.记生产商风险为α，消费者风险为 β (0 ＜α,β＜1),pα,pβ分别代表对应1−α 的接收概率和 1−β 的拒绝概率下的不合格品率，对于给定的pα和pβ，以及最优的s1和 α1，抽样设计的问题就是如何确定抽样所需样本量n以及接收系数d，使其满足生产商和消费者对预期风险的要求.

事实上，对于j=1,2,···,ki在时间段 (ti,j−1,ti j) 内失效的产品数ni j服从条件二项分布，其形式如下

在应力水平si下，一个产品在时间段 (0,ti,j−1) 内未失效而在时间段 (ti,j−1,ti j) 内失效的概率.这样(2)式可以简化为如下形式：

故似然函数可以写为

用 lnL来表示L(β0,β1,σ,p;f1,r1,f2,r2) 的对数，则

其中各元素的具体表达式可通过如下方式获得.

在对数似然函数（3）式中分别对 β0，β1，σ 和p求一阶偏导，记xij=nij，k(i)=ki，可得下列各式：

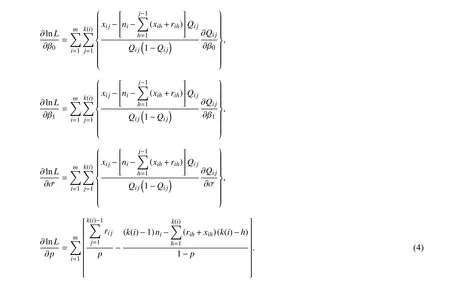
则 β0，β1，σ 和p的极大似然估计可以通过解以上各式等于0 的方程组得到.

为了下一步的推导，需先计算下列式子：

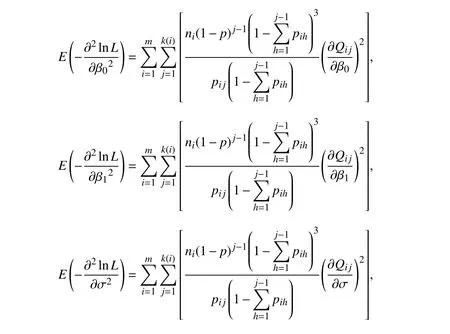
为了获得所需Fisher 信息阵，要对（4）式进一步求各参数的2 阶导数，接着对所得2 阶导数求负的期望，就可得下列各式：

2 试验参数及抽样方案的确定

2.1 应力水平s1和样本分配比例α1 的确定记

2.2 抽样方案中样本量n 和接收系数d 的确定各应力水平的真实值在计算中使用不太方便，所以我们考虑用下面这个公式对其进行变形：其中a0，a1，a2分别代表正常、低应力、高应力水平.这样s0=0,s2=1，并且有 0 ＜s1＜1.

在生产中，一批合格产品有可能被当作不合格产品被拒收，这个把合格产品批当作不合格产品批拒收的概率称为第一类错判概率，也称为生产商风险，记为 α；同理，一批不合格品也可能被接收，这个把不合格产品批当作合格产品批接收的概率称为第二类错判概率，也称为消费者风险，记为 β.当产品的不合格品率e≤pα时，消费者应该以至少 1−α 的概率接收这批产品，而当产品的不合格品率e≥pβ时，消费者应该以至多 β 的概率接收这批产品，或者说至少以 1−β 的概率拒绝这批产品.用数学公式可以分别表达为：P(T≥C′|e≤pα)≥1−α，P(T≥C′|e≥pβ)≥β.由于OC 曲线过 (pα,1−α) 和 (pβ,β) 这2 个点，所以将这2 点的坐标代入（5）式可得到

联立（6）和（7）式可解得

这里zx是标准正态分布的x分位数，wy是对数寿命分布的y分位数，即标准正态分布的y分位数.

2.3 β0，β1的确定假定Pu=P{一个产品正常应力水平下在时间段(0，tc=1)内失效}，Ph=P{一个产品高应力水平下在时间段 (0，tc=1)内失效}，通过（1）式中所提供的函数，我们可以得到：

3 数值结果及分析

本文中，观测时刻点tij的选取采用等间隔观测，因其操作方便，在实际应用中被广泛采用.用tij表示第i个水平下的第j次观测时刻，取i=1,2,j=1,2,···,k.设定观测截止时刻点tci=1，则有tij=其形式相当简单，而且一旦总观测次数k的值确定，所有的tij都可随之确定，非常方便.

在计算过程中，我们采用网格点搜索的方法，首先在 (0,1)×(0,1) 的区域上，等分10，000 个网格，每个网格的坐标都对应一对 (s1,α1) 的值，计算v0在每一对 (s1,α1) 上所对应的值，并通过比较选取其中使v0达到最小的 (s1,α1) 作为最优值，记为然后利用已经得到的的值，我们可以通过（8）式计算接收系数d，通过（9）式确定需要的样本量n*.

在计算中，我们分别考虑了2 应力水平下截尾时间是1∶1 和1∶0.5 的2 种情况，k分别取2，3，5 和10，p分别取0，0.1，0.3 和0.8.当取Pu=0.01 和Pu=0.1 时，Ph分别取0.5 和0.9.特别在p=0 时，表示加速寿命试验在没有移走的定时截尾模型下的抽样方案.计算结果分别在表1 和表2 中给出.

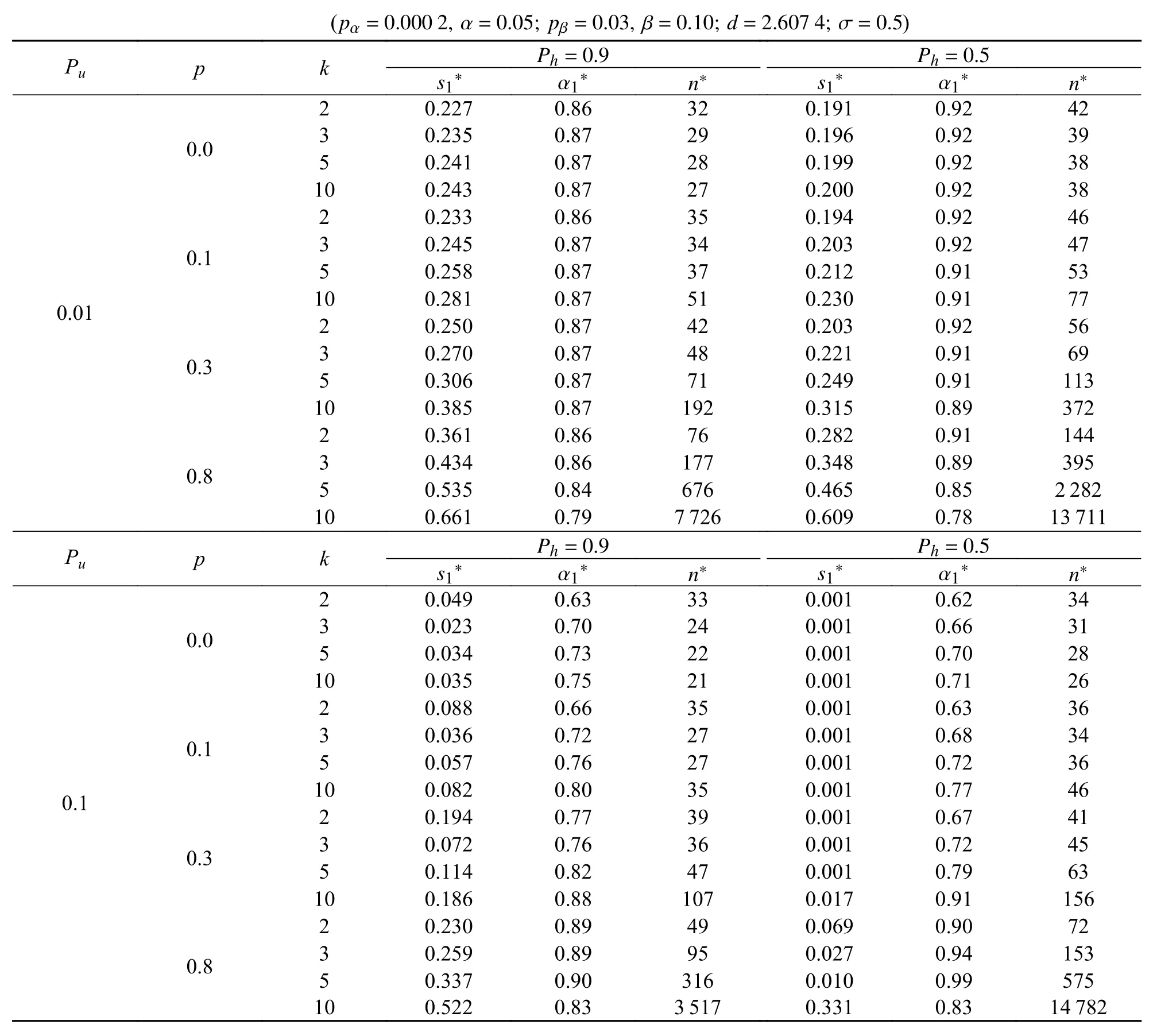
表1 等间隔观测下的抽样方案（截尾时间（1∶1））Tab.1 Sampling plans with equal space（Censoring time（1∶1））

表2 等间隔观测下的抽样方案（截尾时间（1∶0.5））Tab.2 Sampling plans with equal space（Censoring time（1∶0.5））

计算结果表明：对于给定的Pu和Ph，在没有随机移走（p=0）的情况下，通过增加观测次数可以减少样本量；在低移走概率（p=0.1 和p=0.3）的大多数情况下，随着观测次数k的增加，样本量n*先减后增，在中间达到了一个平衡；而在高移走概率（p=0.8）的情况下，随着观测次数k的增加样本量n*迅速增加.因此我们在进行抽样检验时可遵循这一规律进行如下操作：在无移走和低移走的情况下，应该适度增加观测次数k；而在高移走的情况下，应当尽量减少观测次数k.

对于给定的Pu，在观测次数k相同的情况下，Ph大的对应的最优低应力水平也较高，分配在下的最优样本比例较小，样本量也相对较小.这说明在较高的应力水平下产品失效更快，试验的效果更好.而对于给定的Ph，Pu的变化所带来的影响较小.

对比表1 和表2，在1∶0.5 截尾下的s∗1 明显小于1∶1 的Ph=0.9 时，2 种情况下所需的样本量差别不大，而当Ph=0.5 时，前者所需样本量明显较大.

4 结论

针对对数正态分布下伴有随机移走的定时截尾恒加寿命试验模型，我们对等间隔观测方式下的抽样方案进行了研究.利用数值模拟的方法，对不同的参数组合得到了对应的抽样方案.对于不同的情况，抽样方案中的样本量都会有变化，但总体说来，选择合适的移走概率p和恰当的观测间隔对于产品寿命的准确估计会有很大帮助，也能有效降低试验所需样本量.在具体的试验中，我们应该尽量避免过高的移走概率，适度加大高应力水平s2的值，并增加在其水平下进行试验的样本量，缩短高应力水平下两观测点之间的间隔时间，而低应力水平的取值也应该明显高于正常水平.