星-地混合通信网络前向链路安全传输方案研究

金 鑫，任保全，李洪钧,，巩向武，董飞鸿

(1. 军事科学院国防科技创新研究院，北京 100071；2. 军事科学院系统工程研究院，北京 100141；3. 航天工程大学航天信息学院，北京 101416)

0 引 言

无线通信的广播特性，使得处于无线通信范围内的窃听节点能够侦听到无线传输信号[1]。卫星通信网络的广域覆盖特性及广播特性[2-3]，无论是民用通信还是军用通信都潜在被窃听的安全威胁[4]。卫星通信网络中传统的安全通信技术主要通过网络层或数据层加密实现[5-6]。然而，由于星载处理器和卫星通信终端的计算能力有限，无法利用高复杂的加密方案实现绝对的信息安全[7-8]。同时，由于卫星窃听节点不发送信号即可窃听卫星信号，卫星通信网络中的合法节点和信关站完全无法获知卫星窃听节点的信道状态信息(Channel state information, CSI)，不能对其进行主动干扰。近年来，物理层安全技术成为实现无线通信安全的研究热点之一，其能够充分利用物理层资源实现无线通信的安全传输。

保密速率的计算通常需要获知窃听链路CSI，但是该信息在被动窃听情况下是不可获取的[9]。物理层安全从信息论的角度，在未知窃听信道时能够最大程度地恶化窃听节点的接收信号质量[10]，同时确保合法节点的接收信号质量。文献[11]提出了利用协同干扰的安全传输方案用来增强地面无线通信网络的安全传输，由于安全传输方案只需要获知网络中的合法节点的CSI，因此，物理层安全技术具备解决卫星通信网络安全传输的可行性和优越性。如果只利用卫星通信终端或星载天线，直射信道的特征导致无法实现物理层安全传输的方案，文献[12-13]对于卫星通信的传输方案研究中就没有考虑安全问题。

目前，地面MIMO(Multiple input multiple output)通信和中继协同通信中的物理层安全通信技术有较多的深入研究[14]，卫星通信传输方案中关于物理层安全技术的研究相对有限。文献[15]分析研究了卫星通信网络中保密速率约束下的功率控制和波束成形方案。通过假设窃听节点非理想CSI或者部分非理想CSI，文献[16]设计了卫星发射功率最小化的安全传输方案。然而，文献[15-16]没有考虑地面通信网络协同干扰问题。随着无线传输容量需求的快速增长，无线频谱日益短缺，文献[17-18]提出将频谱认知引入到星-地混合通信网络中。这种场景中，地面基站与卫星前向链路共用频谱资源，以实现频谱的高效利用。文献[19]分析研究了星上发射功率分配和下行波束成形联合优化方法，构建以保密速率为目标的优化模型，改进ZF(Zero-forcing)算法求解波束成形权值向量，将非法窃听节点方向接收功率置零。但是，对于星-地混合通信网络中的安全传输问题的研究较少。文献[20]研究了窃听信道未知情况下，基站到卫星合法节点之间的信道有误差时的中断概率和保密速率，没有考虑非理想CSI下的安全传输方案。当前，星-地混合通信网络已经纳入到了5G融合与天地一体化发展中[21-22]，因此，分析研究星-地混合通信网络的安全传输方案具有重要的现实意义。

本文针对星-地混合通信网络前向链路安全传输问题展开研究，分别设计了部分非理想CSI和非理想CSI下的安全传输方案，提出一种将地面基站发送信号作为一种协同干扰，通过引入基站发送干扰信号来恶化卫星窃听节点的接收性能。优化目标为地面基站节点传输速率最大，确保卫星合法节点接收信号质量，同时利用地面基站发送信号阻塞卫星窃听节点对卫星信号的侦听。仿真校验结果表明，该方案能够降低网络对CSI误差的敏感性，提高网络的可靠性和保密性。

1 网络模型

大部分窃听场景中，发送者无法获知窃听信道信息，特别是被动窃听的情况，对于卫星通信场景尤为如此，在不发送信号的条件下，卫星窃听节点的CSI和位置完全无法获得。因此，本节考虑将地面基站作为协同干扰节点，以地面基站节点通信速率最大为优化目标，始终确保卫星合法节点的信干噪比SINR(Signal to interference and noise ratio)，通过最大化基站发射功率来恶化阻塞卫星窃听节点的接收信号质量。

图1 存在窃听链路的星-地混合通信网络Fig.1 Hybrid satellitE-terrestrial communications networks with eavesdropping link

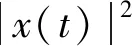
卫星合法节点，卫星窃听节点，地面基站节点的接收信号分别表示为：

(1)

(2)

(3)

卫星合法节点和窃听节点接收信干噪比γi为：

(4)

地面基站节点接收信干噪比γs为：

(5)

卫星通信与地面基站通信的重要区别就在于信道特征不同，因此，下文将对卫星信道特征进行分析。

1)波束增益

卫星用户节点到卫星的信道特征主要取决于卫星天线波束方向图和用户地理位置。用户位置由波束中心到接收机位置的角度θ决定，其与卫星点波束3 dB衰落的角度θ3 dB相关。波束增益近似为[23]：

(6)

其中，μ=2.07123sinθ/sinθ3 dB，φ为卫星合法节点与波束中心之间的角度，θ3 dB为3 dB衰落角度。J1和J3分别是第一类Bessel函数的序列1和序列3：

(7)

2)信道衰落分布

(8)

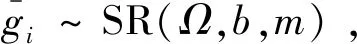
(9)

地面无线通信信道hi(is,e,p)为Rayleigh衰落信道模型，采用典型的Kronecker模型[20]，地面无线通信信道向量表示为：其中，向量元素为独立同分布i.i.d.(independent and identically distributed)复高斯随机变量，即，C(0,1),j=1,2,…,N，(·)T表示转置运算符。

2 未知窃听信道下的安全传输方案

通过分析研究未知窃听信道下的安全传输方案，假设地面基站节点链路是理想CSI，卫星合法节点链路为非理想CSI，由于CSI误差导致安全性能的恶化，因此，设计具有鲁棒性的安全传输方案，既能满足卫星合法节点SINR又可以对抗非理想CSI的影响。

2.1 部分非理想CSI下的安全传输方案

本节提出一种波束成形方案确保地面基站节点能够与卫星网络的前向链路共享频段。在未知窃听节点CSI的情况下，为了最大程度的恶化潜在窃听节点接收质量，网络优化目标是最大化地面基站节点的传输速率，同时满足卫星合法节点的SINR和基站功率约束pmax的条件下，最大化基站发射功率以达到干扰潜在窃听节点的目的，从而增强网络的安全性能。这个问题等价于在同样的约束条件下，最大化基站发射有用信号的功率。在实际通信中，由于信道衰落等因素，合法节点获得的CSI会存在误差，本节从实际出发，给出基站到卫星合法节点的CSI误差，并建立鲁棒性安全传输的优化模型。

在地面基站通信网络中，地面基站到地面基站节点的信道可以通过训练序列估计hs，当信干噪比非常高时，hs能够接近完美。但是地面基站到卫星合法节点的信道hp没有反馈链路，因此，地面基站到卫星合法节点的信道hp是非理想信道。

部分非理想CSI只考虑地面基站到卫星合法节点信道hp为非理想的情况，构建hp误差模型为：

(10)

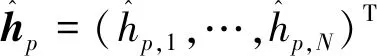
(11)

在部分非理想CSI情况下，卫星合法节点的接收信干噪比γp1表示为：

(12)

地面基站节点的接收信干噪比γs1表示为：

(13)

在部分非理想的CSI情况下，提出优化目标为地面基站节点传输速率最大，由于地面基站到卫星合法节点的信道hp为构建的非理想CSI误差模型，且卫星合法节点的最小SINR必须大于门限值，同时基站发射功率受限。部分非理想CSI下安全传输方案的优化模型表示为：

ps≤pmax

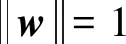
(14)

其中，γ表示卫星合法节点能够实现可靠通信情况下的接收SINR门限值。优化模型(14)的第一个约束条件保证了在出现CSI误差情况下卫星合法节点的正常通信。将优化模型(14)的第一个约束称为卫星合法节点的最低接收SINR约束或者最差接收SINR约束。

同样，由于log2(·)是一个递增函数，并将卫星合法节点的接收γp1代入式(14)，优化模型转换为：

ps≤pmax

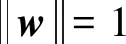
(15)

优化模型(15)的第一个约束条件满足以下不等式：

(16)

通过式(16)将式(15)转换为以下优化模型：

ps≤pmax

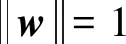
(17)

从信道误差的角度，将优化模型(17)转换为：

ps≤pmax

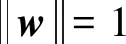
(18)

将优化模型(18)中的第一个约束条件表示为：

(19)

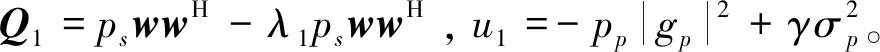
利用S-Procedure原理[24]对优化模型(18)进行求解，因此，约束条件式(19)重新表示为：

β1≥0

(20)

为了求解优化模型(18)，引入半正定松弛SDR(Semi-definite relaxation)原理[25]。定义最优波束成形矩阵权重W=wwH，通过式(20)将优化模型式(18)转换为以下模型：

ps≤pmax

tr(W)=1

rank(W)=1

(21)

根据SDR原理，忽略式(15)中的第四个非凸约束条件rank(W)=1，则优化模型(21)松弛为：

ps≤pmax

tr(W)=1

(22)

由于式(22)中的变量为地面基站发送信号功率ps和波束成形矩阵权重W，本节采用迭代优化算法对该优化模型进行求解。首先固定地面基站发送信号功率ps，求解最优波束成形矩阵权重W；然后，根据第一步求解得到的波束成形矩阵权重W，再次迭代求解最优的地面基站发送信号功率ps。

从式(22)看出，在固定地面基站发送信号功率ps时，其可以转化为一个半正定规划SDP(Semi-definite programming)问题[25]，由于SDP问题归属于凸问题，表1给出了求解式(22)的迭代优化算法，其中δ表示计算精度。

表1 迭代优化算法Table 1 Iterative optimal algorithm

然而，通过SDR原理求解得到的波束成形矩阵权重W，无法确保其秩始终为1，因此，此时求解得到的最优波束成形矩阵权重W只能作为优化模型(14)的一个次优解，通过进一步处理解决最优波束成形矩阵权重W的秩始终为1的问题。利用高斯随机(Gaussian randomization)算法将迭代优化算法求解得到的最优波束成形矩阵权重W转化为式(14)的逼近解。同时，如果高斯随机化后得到的最优波束成形矩阵权重W的秩为1，则可以将W分解得到最优预编码向量w。

表2 高斯随机算法Table 2 Gaussian Randomization algorithm

2.2 非理想CSI下的安全传输方案

非理想CSI考虑地面基站到卫星合法节点、地面基站节点信道hp，hs均为非理想的情况，构建hp，hs误差模型为：

(23)

(24)

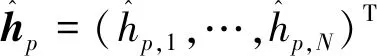
(25)

在非理想CSI下，卫星合法节点的接收信干噪比γp2表示为：

(26)

地面基站节点的接收信干噪比γs2表示为：

(27)

如果在地面基站到卫星合法节点、地面基站节点的链路均为非理想CSI下，仍然采用第2.1节求解方法，会直接恶化卫星合法节点的接收性能。因此，必须进一步研究非理想CSI下的安全传输技术。在非理想CSI下提出的优化目标为使得基站最小SINR的用户传输速率最大，卫星合法节点中的最小SINR须大于门限值，同时基站发射功率受限。非理想CSI下安全传输方案的优化模型表示为：

ps≤pmax

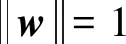
(28)

其中，γ表示卫星合法节点能够实现可靠通信情况下的接收SINR门限值。同样，优化模型(28)的第一个约束条件保证了在出现CSI误差情况下卫星合法节点的正常通信。将式(28)的第一个约束称为卫星合法节点的最低接收SINR约束或者最差接收SINR约束。

将卫星合法节点的接收SINR代入优化模型(28)，因此，式(28)转换为：

ps≤pmax

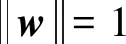
(29)

令：

(30)

则将优化模型(29)转换为：

ps≤pmax

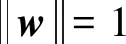
(31)

将优化模型(31)中的第二个约束条件重新表示为：

(32)

根据S-Procedure原理[24]，式(32)重新表示为：

β2≥0

(33)

为了求解模型(31)，引入SDR原理。定义W=wwH，并将式(20)和式(33)带入式(31)，将优化模型(31)重新转化为：

ps≤pmax

tr(W)=1

rank(W)=1

(34)

根据SDR原理，忽略优化模型(34)中的第五个非凸约束条件rank(W)=1，则将优化模型(34)松弛为：

ps≤pmax

tr(W)=1

(35)

对于实数ξ，优化模型(35)归属于SDP问题，因为SDP问题是凸的，因此采用内点法对SDP问题进行求解，则式(35)转化为凸问题：

FindW

ps≤pmax

tr(W)=1

(36)

优化模型(36)可以通过二分搜索算法进行求解，表3表示了二分搜索法的具体过程。其中，SDP可行性求解主要用于判断模型的可行性。

表3 二分搜索算法Table 3 Binary search algorithm

二分搜索算法首先假设优化模型(36)为可行性的，初始区间为[ξl,ξu]，并确保最优值ξ*在这个初始区间内。然后，以中点(ξl+ξu)/2求解凸的可行性问题，判断在中点的上区间还是下区间，不断迭代更新ξ*以确保所在区间足够小，迭代过程中始终确保最优值ξl≤ξ*≤ξu在区间[ξl,ξu]。通过SDR原理求解得到的波束成形矩阵权重W，无法确保其秩始终为1，因此，此时求解得到的最优波束成形矩阵权重W只能作为优化模型式(28)的一个次优解，通过进一步处理解决最优波束成形矩阵权重W的秩始终为1的问题。利用表2的高斯随机法将二分搜索算法求解得到的最优波束成形矩阵权重W转化为优化模型式(28)的逼近解。同时，如果高斯随机化后得到的最优波束成形矩阵权重W的秩为1，则可以将W分解得到最优预编码向量w。

3 仿真校验

图2研究了基站发射功率对于保密速率的影响。对于部分非理想CSI、非理想CSI下的安全传输方案中，CSI误差分别为0.01和0.1，基站天线数量N=4，卫星合法节点接收门限SINR=0 dB。仿真校验结果表明，基站功率约束Pmax=45 dBm时，非理想CSI(误差0.1)、部分非理想CSI(误差0.1)、理想CSI下的保密速率比只考虑卫星方案分别高出约2.4bit/(s·Hz)、3.6bit/(s·Hz)、5.2bit/(s·Hz)，理想CSI下的保密速率明显高于部分非理想CSI和非理想CSI的保密速率，卫星合法节点的保密速率随着基站发射功率的增加而增加，其原因在于，在确保卫星合法节点的SINR的同时，基站发射功率会干扰卫星窃听节点的卫星信号接收质量，同时保密速率会随着地面基站功率的增大而收敛。从部分非理想CSI和非理想CSI的保密速率来看，信道误差明显影响了保密速率的性能。在没有星-地协同及窃听信道CSI未知的情况下，卫星合法节点的保密速率始终为定值。通过仿真校验对比说明，星-地混合通信网络的保密速率优于卫星通信网络的保密速率。

图2 基站发射功率约束对于保密速率的影响Fig.2 Transmit power constraint of base station impacts on secrecy rate

图3研究了卫星合法节点最小SINR门限对于保密速率的影响。对于部分非理想CSI下、非理想CSI下的安全传输方案中，CSI误差均为0.01，Pmax=40 dBm，基站天线数量N=4。仿真校验结果表明，卫星合法节点最小信干噪比为6 dB时，非理想CSI(误差0.01)、部分非理想CSI(误差0.01)、理想CSI下的保密速率比只考虑卫星方案分别高出约1.2bit/(s·Hz)、2.2bit/(s·Hz)、2.7bit/(s·Hz)，理想CSI下的保密速率明显高于部分非理想CSI和非理想CSI的保密速率，卫星合法节点的保密速率随着最小SINR门限的增加而减小，其原因在于，卫星合法节点的最小SINR的提升直接导致保密速率的降低。信道误差明显影响了保密速率的性能。在没有星-地通信网络协同的情况下，卫星合法节点的保密速率趋于定值。

图3 卫星合法节点最小信干噪比对于保密速率的影响Fig.3 Minimum signal to interference and noise ratio of satellite legitimate node impacts on secrecy rate

图4研究了CSI误差对于保密速率的影响。对于部分非理想CSI、非理想CSI下的安全传输方案中，Pmax=40 dBm，卫星合法节点的最小SINR从1 dB增加到5 dB，基站天线数量N=4。仿真校验结果表明，CSI误差为0.06时，非理想CSI比部分非理想CSI(最小SINR门限从1～5 dB)分别降低约0.6bit/(s·Hz)、0.7bit/(s·Hz)、0.9bit/(s·Hz)、1.1bit/(s·Hz)、1.2bit/(s·Hz)，部分非理想CSI下的安全性能要优于非理想CSI下的安全性能，卫星合法节点的保密速率随着最小SINR门限的增加而减小，其原因在于，卫星合法节点的最小SINR的提升直接导致保密速率公式中保密速率的降低。卫星合法节点的保密速率随着信道误差的增加而减小，信道误差明显影响了保密速率的性能。其原因在于，根据保密速率公式合法链路非理想CSI造成的噪声泄漏，要求地面基站发射额外的发射功率给地面基站节点，同时增加对卫星合法节点和卫星窃听节点的干扰。

图4 非理想信道状态信息误差对于保密速率的影响Fig.4 Imperfect channel state information error impacts on secrecy rate

4 结 论

本文针对星-地混合通信网络前向链路存在卫星窃听链路的安全问题，分别设计了部分非理想CSI和非理想CSI下的安全传输方案，提出一种将地面基站发送信号作为一种协同干扰，通过引入地面基站发送信号来恶化卫星窃听节点的接收性能。仿真校验结果表明，卫星合法节点的保密速率随着最小信干噪比门限的增加而减小，随着信道误差的增加而减小，采用协同干扰方案下的保密速率优于未考虑协同干扰的保密速率，提出方案能够降低网络对CSI误差的敏感性，提高网络的可靠性和保密性。