基于多圆锥曲线法的着陆器奔月轨道设计与特性分析

杨路易，李海阳，张 进，周晚萌

(国防科技大学空天科学学院，长沙 410073)

0 引 言

1969年7月20日，阿波罗11号的航天员阿姆斯特朗迈出了人类登上月球的第一步，载入人类史册[1]。近些年来月球探测和科学研究不断升温，掀起了又一轮热潮。2017年10月特朗普政府宣布将重启载人登月计划，并计划发射名为“深空之门”的月球空间站，为未来火星探测任务提供支撑[2-3]。2019年1月，中国成功发射嫦娥四号，实现了人类首次的月球背面探测[4]。

载人月球探测任务是一项复杂的系统工程，其中的核心问题之一为地月转移轨道设计。航天器在地月空间内会受到多个中心引力体、非球形摄动以及太阳光压的影响，力学环境较为复杂。郑爱武等[5]结合实际工程介绍了载人登月任务的轨道设计方法、约束条件和飞行模式等。彭坤等[6]介绍了利用地月空间站出发的6种载人登月飞行模式。高玉东等[7]基于B平面瞄准和分层搜索思想提出了一种地月转移轨道快速设计方法。周文艳等[8]分析了月球终端为环月极轨道的地月转移轨道特性，并介绍了嫦娥二号卫星的轨道设计方法。贺波勇等[9]针对环月轨道交会,提出三层逐级求解策略设计着陆器(Lunar module,LM)奔月轨道，并考虑了自由返回轨道的奔月工况[10]。黄文德等[11]基于双二体模型研究了自由返回轨道的设计流程并分析了轨道基本特性。Peng等[12]进一步分析了自由返回轨道的月面可达域特性。张磊等[13]以双二体模型计算结果为初值，研究了地月自由返回轨道的高精度设计方法。

以上大多数研究基于双二体模型，对地月转移轨道进行优化求解。但是该方法精度有限，当飞行时间大于114 h后，模型精度几乎失效[14]。多圆锥曲线法是Wilson[15]和Bynes等[16]在1970年左右提出的一种近似解析计算地月转移轨道的方法，其计算时间约为高精度模型的10%，误差只有双二体拼接法的1%，具有计算速度快、精度较高的显著优势。Luo等[17]结合微分修正法与多圆锥曲线法设计了自由返回轨道。Li等[18]利用多圆锥曲线法构造了多段自由返回轨道的解析表达式。Zhang等[19]利用多圆锥曲线提出了一种自由返回轨道的快速设计方法。可以发现，近年来多圆锥曲线法作为一种快速轨道设计方法，受到了不少学者广泛关注。

对于着陆器地月转移轨道的求解，目前研究有两个方面需要改进：1)基于双二体解析模型的轨道参数特性分析，精度有限；2)奔月窗口采取多点打靶法进行求解，策略繁琐复杂且效率较低。本文将基于多圆锥曲线法设计着陆器地月转移轨道，以提高轨道初始设计精度。同时，将出发轨道在地心白道系下进行轨道参数转换，通过打靶分析和数据拟合相结合，发现着陆器的奔月轨道特性和窗口特性的变化规律。

1 问题描述

1.1 问题提出

受限于火箭运载能力以及载人飞船人员安全性的要求，李祯等[20]提出了人货分运的飞行模式。该飞行模式中，载人飞船和着陆器分别运送到近地停泊轨道(Low Earth orbit,LEO)，其中载人飞船采取飞行时间3天左右的自由返回轨道，而着陆器采取3～5天的低能量地月转移轨道，两者先后到达环月轨道(Low lunar orbit,LLO) 进行交会对接。对于5天左右的奔月轨道，双二体模型的计算精度不再可用，而利用高精度模型进行可达域分析和窗口分析时效率太低。

因此，本文选择多圆锥曲线法来研究着陆器的地月转移轨道特性和窗口特性，其轨道类型不受限于自由返回轨道的安全性约束。着陆器首先位于近地停泊圆轨道LEO，在合适位置A点，施加共面切向脉冲vA加速，进入地月大椭圆转移轨道(Lunar transfer orbit,LTO)；到达近月点B点后，施加共面切向脉冲vB制动，进入环月圆轨道LLO。整个飞行过程如图1所示。

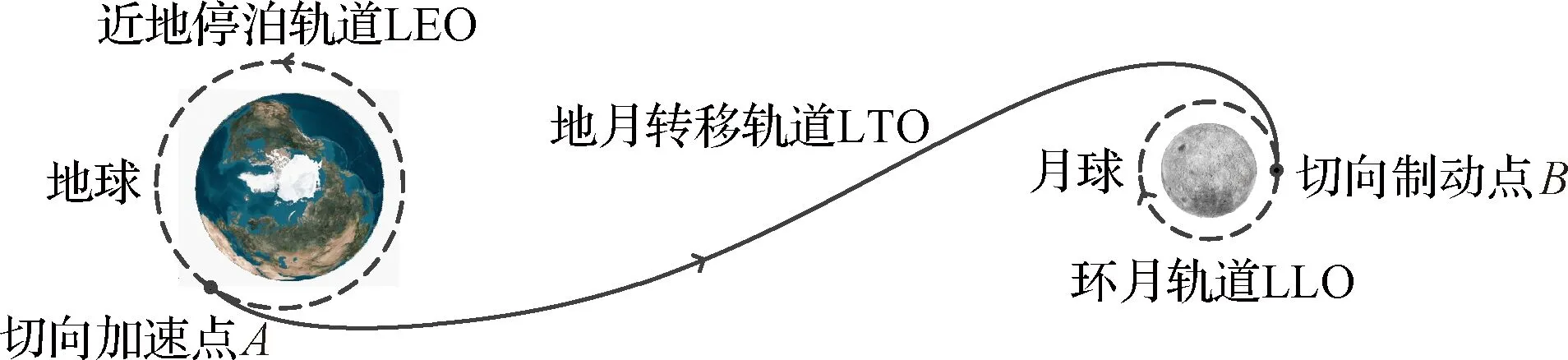
图1 着陆器地月转移轨道示意图Fig.1 Sketch of LM trans-lunar trajectory

1.2 设计变量选择

假设LEO和LLO均为圆轨道，则轨道的形状和轨道相对于中心引力场的位置可以简化为3个参数(h,Ω,i)，其中h为轨道高度，Ω为升交点赤经，i为轨道倾角。若LEO上述三个轨道根数已知，则对于地月转移轨道，设计变量可以选择为切向速度脉冲大小vA，加速点A纬度幅角u，出发时刻tTLI。

已知该3个参数，便可以唯一确定一条LTO轨道。根据目标LLO的不同轨道高度hLLO和轨道倾角iLLO，对LTO进行分类，目标函数的选取为

(1)

本文采取成熟的序列二次规划法(Sequential quadratic programming,SQP)对上述问题进行寻优求解。但是算法的计算效果和收敛性依赖于动力学模型和设计变量初值的选择。若设计变量初值选择不当，SQP算法将难以收敛。因此接下来将介绍多圆锥曲线法并引入地心白道系，通过将出发轨道参数转化为伪倾角和伪升交点赤经，以对设计变量的初值进行较好估计。

2 轨道动力学模型与地心白道系初值估计

2.1 轨道动力学模型

首先简要介绍一下飞行时间TAB已知时，多圆锥曲线拼接法的设计步骤[15]。

图2 多圆锥曲线法示意图Fig.2 Trajectory of multi-conic method

设出发时刻飞行器在地心惯性系下的位置和速度分别为rE,vE，将飞行时间TAB分为N份，在每段时间区间[ti,tf]内：

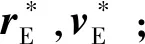
(2)计算[ti,tf]内月球和太阳的平均摄动加速度aM和aS；

(3)修正步骤(1)中得到的二体外推状态

(2)

(4)将修正后的地心状态转化为月心状态rM,vM后，反向线性外推，得到“无引力场”轨道

(3)

重复上述步骤(1)～(5)，便可得到飞行时间TAB结束时的运动状态。

2.2 地心白道系参数转换与初值估计

1)轨道根数转换

引入地心白道系，如图3所示，地球位于O点，A点为近地加速点，B点为近月制动点。LTO轨道面ACE与白道面交于C点，与赤道面交于E点。白道面与赤道面交于D点。

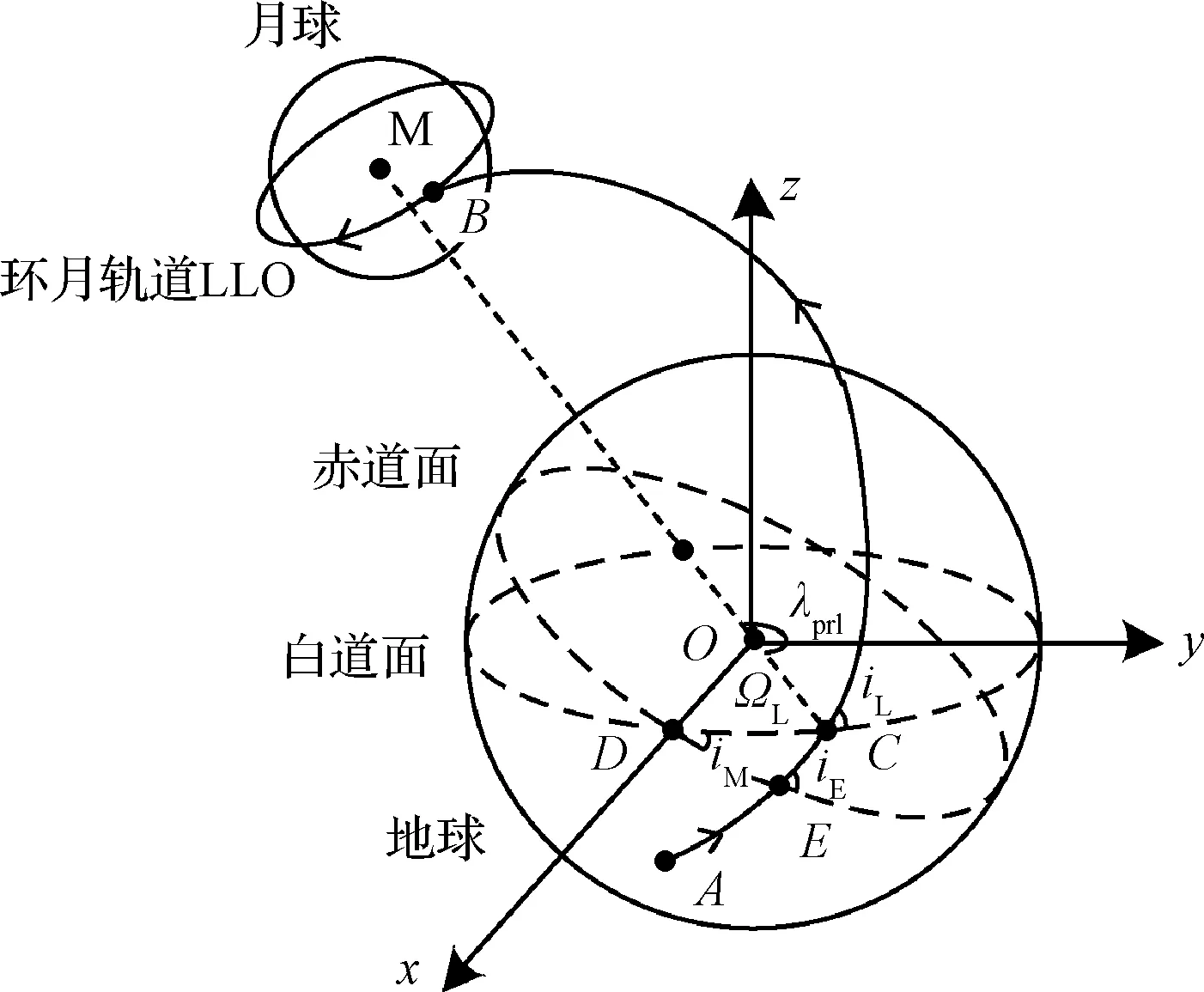
图3 地心白道系下LTO与地月空间关系示意图Fig.3 Sketch of LTO in Earth-centered EMP (Earth-Moon plane coordinate)

为了便于描述LEO、地球、月球的空间关系，考虑将地心惯性系下轨道根数(ΩE,iE)转化为地心白道系下的伪轨道根数(ΩL,iL)，其中ΩL和iL分别称之为伪升交点赤经和伪倾角。

cosiL=-cosiMcos(π-iE)+

siniMsiniEcos(ΩE-ΩM)

(4)

得到iL。

在球面三角形ΔCDE中，利用正弦公式

(5)

得到sinΩL，再利用球面三角形的余弦公式

(6)

结合式(5)，便可得到

(7)

将LEO的轨道倾角iE转化为伪倾角iL，避免了考虑白道面与赤道面夹角iM随着时间的变化而改变(文献[21]介绍，18.6年内变化最小18°18′，最大28°36′)；而将升交点赤经ΩE转化为伪升交点赤经ΩL，有利于对近月点时刻进行初值搜索，这将在下一节进行描述。

2)初值搜索策略

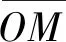
λprl≈180°

(8)

利用式(8)进一步可以估计近月点时刻月球在地心白道系下的升交点赤经

Ωprl(tprl)=ΩL+λprl

(9)

其中,ΩL由式(7)得到。根据式(9)便可以插值得到近月点时刻tprl初值，在给定任务飞行时间TAB后，可以得到奔月出发时刻

tTLI=tprl-TAB

(10)

|uL|≤ΔuL

(11)

该角度uL称之为伪纬度幅角，ΔuL表示其上下界。

在图3中，由几何关系易得

(12)

根据式(5)可以得到

(13)

结合式(11)～式(13)便可以得到惯性系下纬度幅角u满足的约束条件为

(14)

式(8)和式(11)作为重要依据来指导出发时刻tTLI和出发位置u选择，分别称之为伪经度判别准则和伪纬度幅角判别准则。

3 仿真分析

3.1 单条着陆器地月转移轨道求解

首先求解单条优化轨道来校验本文提出的轨道设计方法正确性。假设着陆器出发的LEO轨道的轨道根数如表1所示。

表1 LEO轨道根数Table 1 Orbital elements of LEO

出发时刻搜索为2020年4月1日至2020年4月30日，飞行时间TAB设置为5天。目标函数式(1)中，目标环月轨道高度hLLO=200 km，轨道倾角iLLO=90°，设置vA,uL,λprl搜索范围为

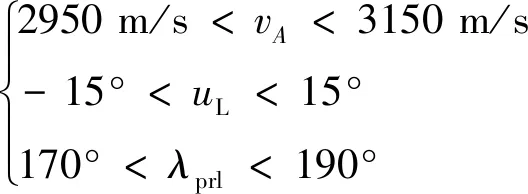
(15)

将式(15)中uL和λprl代入式(9)～(14)，便可得到设计变量u和tTLI的搜索范围。利用SQP算法进行寻优求解时，vA的初值由二体公式提供，uL初值设置为0°，将多圆锥曲线法和高精度模型的求解结果进行对比，结果如表2所示。

结果表明，LEO出发时刻的伪纬度幅角uL=0.65°，近月点到达时刻的伪经度λprl=178.95°，验证了式(8)和式(11)的猜想。对比多圆锥曲线法和高精度模型的计算时间，前者计算仅为0.43 s，后者为58.37 s；对比两种方法的设计变量误差，出发速度ΔvA在3 m/s以内，纬度幅角ΔuL在0.1°以内，出发时刻ΔtTLI在3 min以内。

因此，本文利用多圆锥曲线法，可以对着陆器的地月转移轨道进行快速设计，并且其计算结果能够为高精度模型的精确求解提供较好的初值。在本文的轨道设计方法下，两种动力学模型的设计变量初值相差不大。这是由于地月转移时间较长，当以近地点轨道参数作为设计变量时，近月点轨道根数对近地出发参数的变化较为敏感。

同时，在本文的轨道设计方法下，随机生成200条LEO出发轨道，与不考虑本文给出的初值搜索方法进行对比，收敛性结果如表3所示。式(15)在考虑vA约束条件下，全局搜索策略表示不对uL和λprl施加约束；伪纬度幅角搜索策略表示只对uL约束；伪经度搜索策略只对λprl约束；伪经度+伪纬度幅角搜索策略表示同时对λprl和uL施加约束。可以发现，如果不对设计变量加初值约束，直接利用SQP算法寻优求解，无法获得所求轨道；利用伪经度+伪纬度幅角的搜索方法，收敛率可以提高到100%。单独对比伪经度和伪纬度幅角设计方法，前者对收敛性的影响更大，即近月点时刻的选择更为重要。

表2 不同动力学模型求解结果Table 2 The calculated orbital elements of two methods

表3 不同搜索策略的收敛性对比Table 3 Convergence comparison for different solution strategies

若将目标函数(1)改为只考虑近月点高度约束，将得到环月轨道LLO的轨道倾角iLLO和升交点赤经ΩLLO可达域分布，如图4所示。

图4 地心白道系下LTO与地月空间关系示意图Fig.4 Sketch of LTO in Earth-centered EMP

观察环月轨道的升交点赤经ΩLLO与轨道倾角iLLO的变化，发现两者存在耦合关系，近似成开口向左的环状分布。轨道倾角在20°到160°之间变化，升交点赤经在0°到360°之间变化，这与文献[12,22]的研究结论一致。值得注意的是，这种“开口向左”的性质使得对于同一近月点高度和轨道倾角会存在升交点赤经不同的两个解。

下面将基于多圆锥曲线法动力学模型对不同LEO出发的着陆器地月转移进行快速求解并分析轨道窗口特性。

3.2 近月点窗口宽度Tprl与伪倾角iL关系

文献[10,23]中指出，当LEO倾角大于白赤交角时，一个朔望月内存在两次奔月窗口，但是并未说明单次窗口宽度和LEO之间的具体联系。因此，本节在不同飞行时间TAB、近地出发高度hLEO和目标环月高度hLLO情况下，以地心白道系下伪倾角iL作为特征分析变量，详细分析出发LEO和近月点窗口宽度Tprl之间的内在联系。其中Tprl定义为：飞行器到达LLO制动点位置时，月球位置的可达伪经度范围对应的近月点窗口宽度，即近月点时刻可取值的区间长度。在本节以及后面所有分析中，目标函数(1)只考虑环月轨道高度hLLO约束。

1)飞行时间TAB影响

研究飞行时间TAB不同时，近月点窗口宽度Tprl与iL之间的变化规律。LEO和LLO高度约束设置为hLEO=343 km，hLLO=200 km，飞行天数TAB设置为3～5天。在每个飞行时间下，随机生成36条LEO出发轨道，结果如图5(a)所示。

图5 不同飞行时间下Tprl随iL的变化规律Fig.5 The relationship between Tprl and iL under different flight durations TAB

从图5可以看出，近月点窗口宽度Tprl随着伪倾角iL的增加而减小。且飞行时间TAB不同时，该变化趋势略有差别。若对近月点窗口宽度Tprl与伪倾角iL的关系利用二次多项式进行非线性拟合，可以得到图5(b)所示的二次曲线。

其中，多项式的拟合表达式为

令R表示判定系数，其计算公式为[24]

(16)

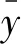
结合图5可以发现，利用二次多项式即抛物线进行拟合，其拟合度R2均在0.99以上。可以认为，近月点窗口宽度Tprl与伪轨道倾角iL存在二次曲线的内在拓扑联系。飞行时间TAB不同的拟合曲线大约相交于iL=40°附近。当iL<40°时，飞行时间越大，近月点窗口越长；当iL>40°时，飞行时间越大，近月点窗口越短。

2) 近地出发高度hLEO影响

研究近地点出发高度hLEO不同时，近月点窗口宽度Tprl与伪轨道倾角iL之间的变化规律。仿真条件设置为TAB=3天，hLLO=200 km。

打靶分析结果和二次多项式拟合结果分别如图6(a)和图6(b)所示。

图6 不同近地出发高度下Tprl随iL的变化规律Fig.6 The relationship between Tprl and iL under different LEO heights hLEO

其中4条曲线的拟合度R2均在0.99以上。可以发现，当伪倾角iL<40°时，近月点窗口宽度Tprl几乎不随出发高度hLEO的变化而变化；当iL>40°时，不同hLEO对应的Tprl才体现出细微差别，但其差别量ΔTprl<0.1 h。因此，认为近地点出发高度hLEO对近月点窗口宽度Tprl影响不大。

3)近月点高度hLLO影响

研究当近月目标高度hLLO不同的时候，近月点窗口宽度Tprl与伪轨道倾角iL之间的关系。仿真条件设置为TAB=3天，hLEO=343 km。

打靶分析结果和二次多项式拟合结果分别如图6(a)和图6(b)所示。

其中3条曲线的拟合度R2均在0.99以上。可以发现，随着近月点高度hLLO的增加，近月点窗口宽度TAB与伪倾角iL之间的二次多项式关系式整体“上移”，呈增大趋势。因此，认为随着近月点高度hLLO增加，近月点窗口宽度Tprl增加。

3.3 加速点纬度幅角uL与伪倾角iL关系

本节分析不同飞行时间TAB、近地出发高度hLEO和目标环月高度hLLO情况下，加速点出发位置uL∈[umin,umax]的变化规律，包括umin，umax和|umax-umin|。其中，umin表示A点加速范围的最小值，umax表示最大值。

1)飞行时间TAB影响

仿真条件设置hLEO=343 km，hLLO=200 km，飞行时间TAB分别设置为3天和5天，加速点A位置[umin,umax]的变化规律如图8(a)和图8(b)所示。

可以发现umin和umax随着iL的增加而增加，但umax-umin随着iL的增加而减小，即加速点A的出发范围越“窄”，这与第3.2节“近月点窗口Tprl随着伪倾角iL增加而减小”结论一致。当TAB为3天时，umin和umax的上下界ΔuL约为9°；当TAB为5天时，ΔuL约为5°，因此验证了伪纬度幅角判别准则式(11)和uL约束条件式(15)。

2)近地出发高度hLEO影响

仿真条件设置TAB=3天，hLLO=200 km，仿真结果如图9(a)和图9(b)所示。

可以发现hLEO越大，对应的umin和umax均增大，有往上“移动”的趋势，但是变化幅度不大。

3)近月点高度hLLO影响

仿真条件设置TAB=3天，hLEO=343 km。结果如图10(a)和图10(b)所示。

图8 不同飞行时间下uL随iL的变化规律Fig.8 The relationship between uL and iL under different flight durations TAB

图9 不同近地出发高度下umin和umax随iL的变化规律Fig.9 The relationship between umin, umax and iL under different LEO heights hLEO

从图10可以发现，近月点到达高度hLLO越大，umax有稍增大趋势，但是变化不明显；而umin无明显变化。

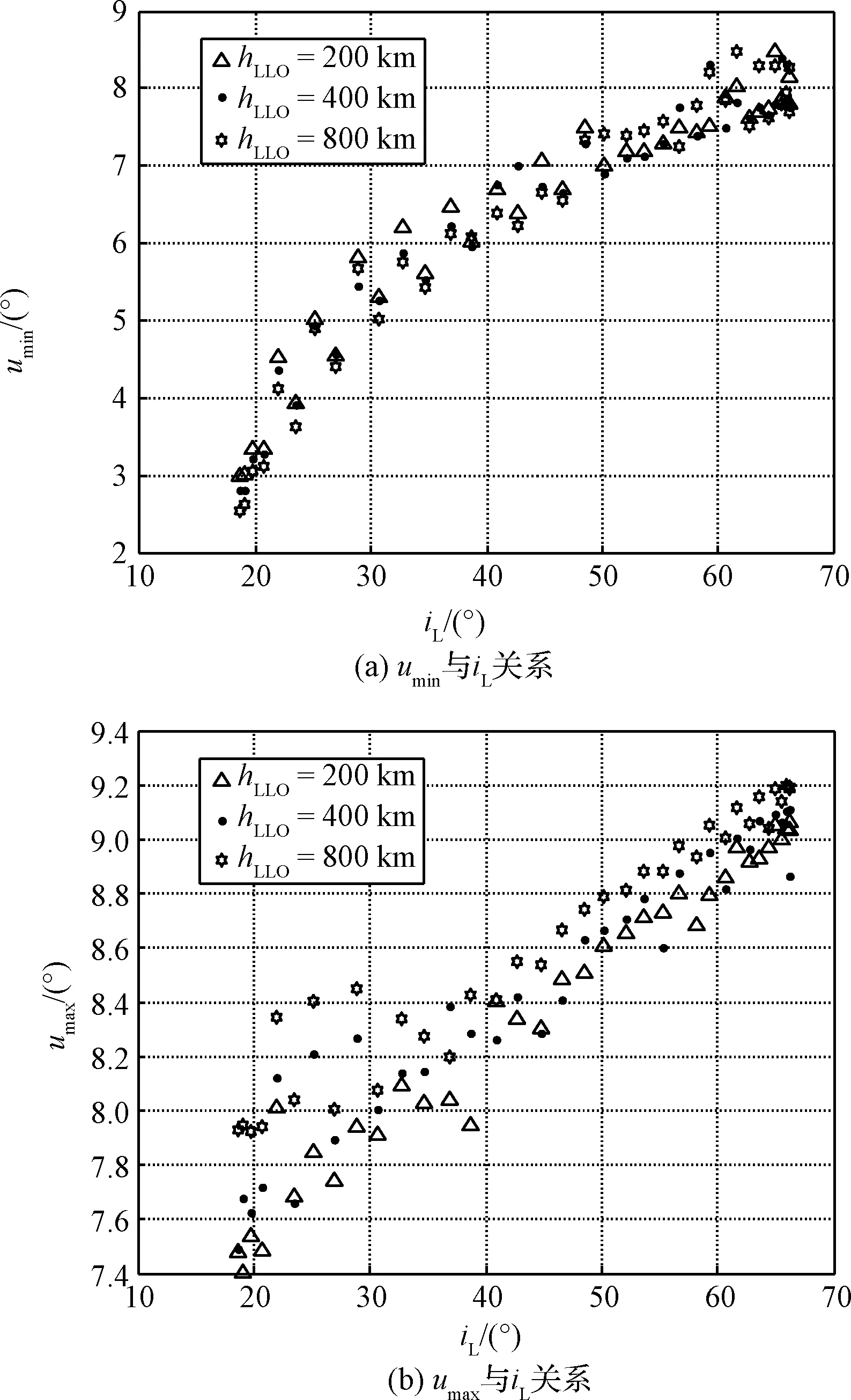
图10 不同近月高度下umin和umax随iL的变化规律Fig.10 The relationship between umin, umax and iL under different LLO heights hLLO

3.4 近地出发速度vA与伪倾角iL关系

本节在不同飞行时间TAB、近地出发高度hLEO和目标环月高度hLLO情况下，分析近地加速点A的出发速度vA变化规律。

1)飞行时间TAB影响

仿真条件设置hLEO=343 km，hLLO=200 km，飞行时间在3天～5天之间变化，计算结果如图11所示。

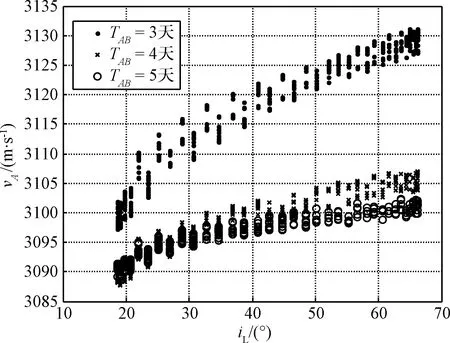
图11 不同飞行时间下vA随iL的变化规律Fig.11 The relationship between vA and iL under different flight durations TAB

图11表明，在相同飞行时间TAB下，出发速度vA随着iL的增大而增大，其变化大小在35 m/s左右。当iL相同时，对于不同飞行时间TAB，vA随TAB的增加而减小，其变化大小在30 m/s左右。

2)近地出发高度hLEO影响

仿真条件设置hLLO=200 km，TAB=3天，近地出发高度在343 km到2100 km之间变化，计算结果如图12所示。

从图12可以发现，出发速度vA随着hLEO的增加而显著减小。当hLEO为343 km时，vA在3120 m/s附近变化；当hLEO为2100 km时，vA在2760 m/s附近变化。

3)近月点高度hLLO影响

仿真条件设置hLEO=343 km，TAB=3天，目标环月高度在200 km到800 km之间变化，结果如图13所示。

图12 不同近地高度下vA随iL的变化规律Fig.12 The relationship between vA and iL under different LEO heights hLEO

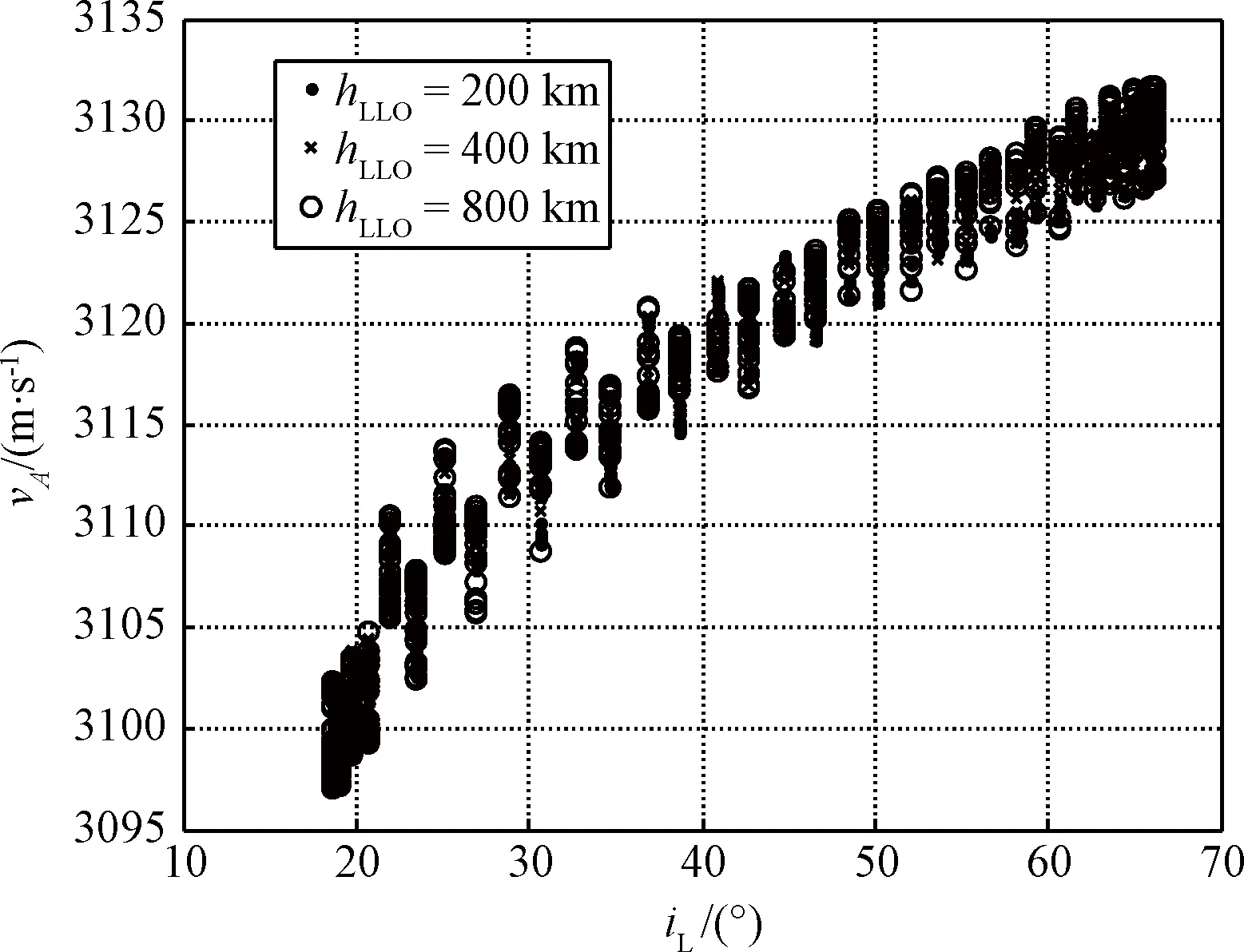
图13 不同近月点高度下vA随iL的变化规律Fig.13 The relationship between vA and iL under different LLO heights hLLO

从图13可以看出，出发速度vA随着hLLO的增加无明显变化。因此，近地出发速度vA大小主要由近地出发高度hLEO决定，同时会受到飞行时间TAB和伪倾角iL的影响。

4 结 论

本文构建了人货分运飞行模式中的着陆器地月转移轨道求解方法，提出的近月点伪经度判别准则能够准确估计近月点时刻，利用多圆锥曲线法能够高效快速求解地月转移轨道，仿真结果表明：

1)提出的近月点伪经度和伪纬度幅角搜索策略，能够准确估计设计变量初值，并快速求解着陆器地月转移轨道，单条轨道的计算时间在1 s以内。

2)多圆锥曲线法的计算结果可以为进一步高精度模型轨道设计提供较好初值参考。

3)以地心白道系为参考坐标系，通过打靶分析与数据拟合相结合，发现了近月点窗口宽度与伪倾角之间的二次多项式拟合关系，同时揭示了近地出发点位置的变化规律。