行星着陆大气进入段自适应滑模抗扰控制方法

戴 娟，苏 中，刘 洪，朱 翠

(1. 高动态导航技术北京市重点实验室，北京 100192；2. 现代测控技术教育部重点实验室，北京 100192；3. 北京信息科技大学自动化学院，北京 100192；4. 北京信息科技大学信息与通信工程学院，北京 100101)

0 引 言

行星探测器安全、精确地着陆到行星表面是开展行星着陆探测任务及采样返回的前提[1-2]，行星着陆过程的快速制导控制是实现安全、精确着陆的基础[3-4]。

未来的行星探测任务对探测器着陆区域的精度有一定的要求，而同时行星探测器在经历最终进入段到达进入点之后，受到行星大气模型不确定、气动环境复杂、强非线性、强耦合等问题的影响，使得着陆精度产生很大的偏差[5-6]。为了满足行星着陆精确性及抗干扰性需求，需要设计考虑行星着陆过程中外部扰动的制导控制方法[6]。火星着陆探测是中国未来深空探测的主要目标，尤其是实现在具有科学价值地区的精确软着陆，然而由于整个着陆过程中存在系统累计误差与环境扰动，因此，有必要进行火星着陆过程中的抗干扰控制研究[7]。

针对行星大气进入段制导控制问题，目前研究算法主要分为两类：预测-校正算法，参考轨迹制导算法[8]。预测校正制导可以跟踪更准确的目标和对初始偏差及干扰不敏感。但由于其对计算量要求较强，限制了其在工程实践中的应用[9]。参考轨迹制导方法在火星大气进入段制导中得到广泛的关注。目前参考轨迹制导方法采用PID、反馈线性化、自适应控制、滑模控制及自抗扰控制等多种方法提高进入制导精度[10-16]。文献[11]研究了刚性航天器在输入幅值和速度均有限制的情况下的姿态跟踪控制问题。采用滑模和扰动观测器应用于估计阻力和阻力速度以及模型误差，该方案采用的是综合反馈线性化的跟踪方案来提供跟踪阻力动力学模型中的模型误差。然而，该方案需要阻力速度的信息，这对于火星大气进入段的着陆器来说，在真实情况下是很难精确测量的。滑模控制可能出现两个主要问题：终端滑模控制系统奇异性问题;传统线性滑模和终端滑模控制都会存在的抖振问题[17-19]。

为了解决存在的问题，研究采用自适应滑模控制方法，自适应滑模控制具有减弱抖振，同时具有避免奇异性的特点。由于着陆过程存在干扰，结合非线性观测器对干扰进行精确估计补偿。因此，自适应滑模控制结合非线性观测器的复合抗干扰控制律可以实现快速、精确跟踪参考轨迹，精确到达预定开伞点，从而提高着陆的安全性。

研究提出一种自适应滑模控制，同时结合非线性观测器的复合抗干扰控制方法。首先建立行星着陆控制模型，引入非线性观测器对未知外界干扰和内部扰动进行估计补偿，利用数学变换推导对行星探测器动力学模型进行优化，引入标称轨迹和实际轨迹的相对距离和相对速度信息进行测量，利用自适应滑模控制律解算探测器的实时倾侧角状态信息，从而获得探测器倾侧角的实时控制指令。最后通过仿真分析探测器开伞点的分布，检验控制算法的有效性。

1 问题描述

假设行星体为一个相对于行星惯性坐标系，绕自转轴做等速旋转的标准圆球，且行星大气是均匀的。行星大气进入段长时间保持超音速飞行，而且高度变化剧烈，因此，在实际的行星探测器大气进入过程中，必须考虑行星自转因素的影响。

行星探测器着陆过程需要用到的参考坐标系，如图1所示。

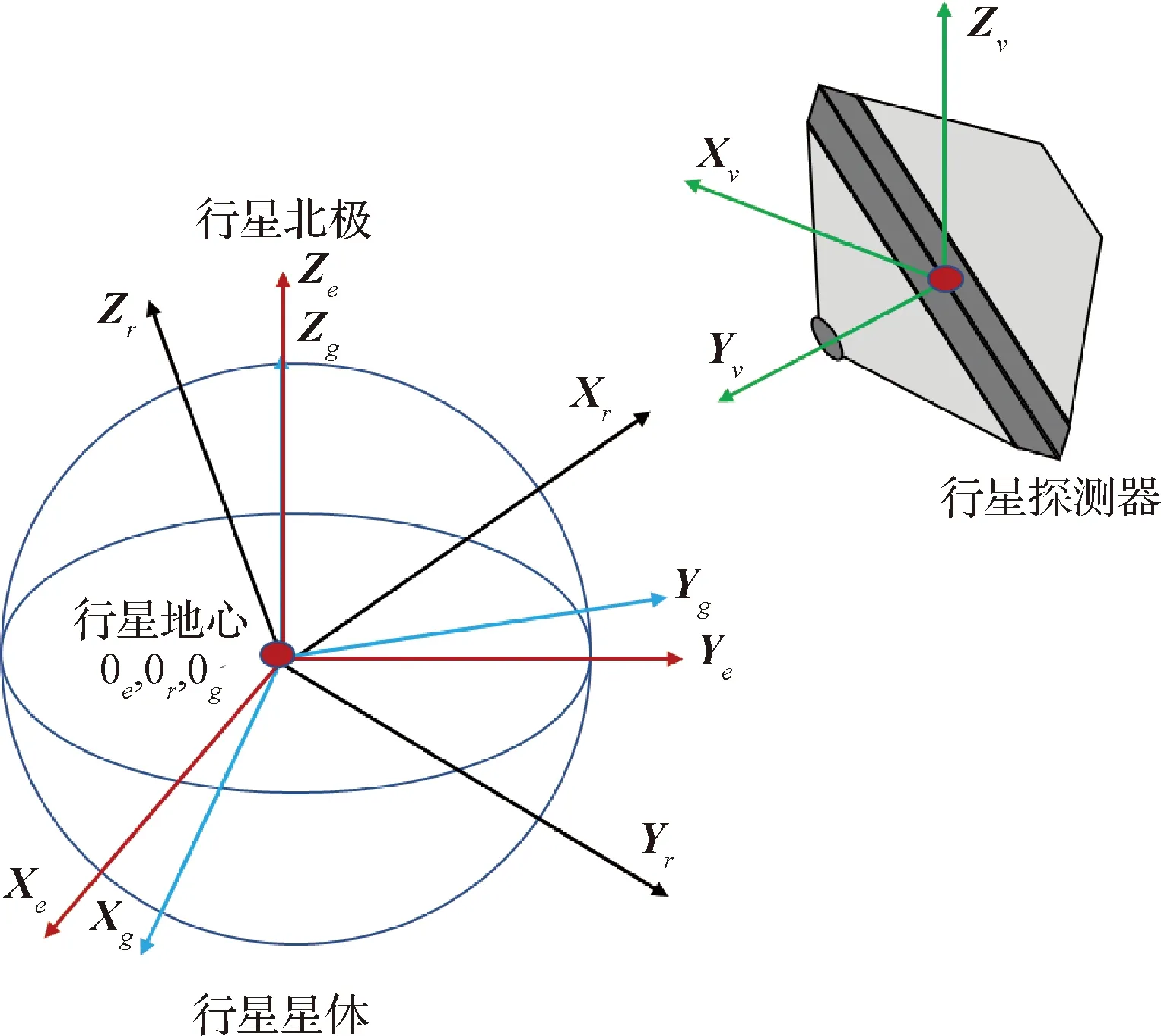
图1 坐标系Fig.1 Coordinates

考虑在有外部扰动的情况下，三自由度的行星探测器动力学模型：

其中，θ为探测器的经度，φ为探测器的纬度，r为探测器到行星球心的距离，V为探测器的速度，γ为探测器的飞行路径角，ψ为探测器的航向角，σ为探测器的倾侧角。L和D为探测器的升力和阻力加速度，定义为：

(2)

此外，式(1)中Cγ和Cψ是由行星自转引起的科氏加速度，定义为

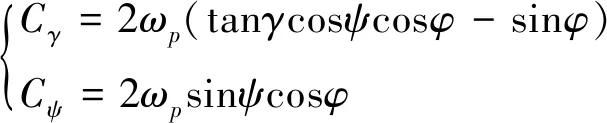
(3)

式中：ωp为行星自转角速率。

2 控制器设计

基于行星探测器动力学模型，考虑行星大气进入段探测器系统在包含大气密度不确定情况下，行星大气进入段轨迹跟踪控制问题。

进入段探测器的位置跟踪误差x1和速度跟踪误差x2定义为：

(4)

式中：r,rd为沿着参考轨迹的探测器到行星球心的距离、期望距离。具体的大气密度不确定为以下形式：ρ=ρ0+Δρ，其中ρ0表示标称的行星大气密度，Δρ表示未知的行星大气密度不确定，气动参数不确定L/D=(L/D)0+Δ(L/D)，(L/D)0为标称的行星探测器升阻比。则可得

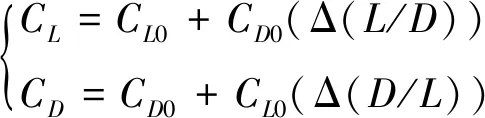
(5)

式中：CD0和CL0为探测器的标称阻力和升力系数。

由式(1)可知，行星大气密度以及探测器气动力系数与动力学系统中气动力模型紧密相关。而在制导控制方法倾侧角指令控制中，不确定参数引起的摄动会随着动力学方程递推传播到行星着陆跟踪控制模型中。

所述的行星着陆跟踪控制系统如下：

(6)

其中，y为系统(6)的输出x1为位置跟踪误差。

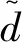
干扰观测器将式(6)中不确定性和外部扰动作为扩张的状态进行估计，干扰观测器的模型为：

(7)

其中，e为观测器的估计误差；y为跟踪系统(6)的输出，是位置跟踪误差；z1,z2,z3为观测器的输出，β01,β02,β03为观测器的增益。函数ffal(·)定义为：

(8)

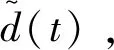
由未知外界干扰和内部扰动引起的总扰动用非线性干扰观测器来进行估计补偿，应用具有自适应的有限时间滑模控制策略，得到控制器如下：

uAda=-(Lcosγ)-1[u*+up(t)]

(9)

式中：

(10)

(11)

其中，式(9)～式(11)中，参数T,kT，k1,k2,α1,α2均为正常数。k1,k2的选择使得多项式k1+k2p依据系统(6)为霍尔维兹多项式，也即，多项式的特征根全部在复平面的左半平面。α1,α2的选择可由以下条件确定[17]：

式中：z3为非线性观测器对外界干扰和内部扰动引起的总扰动的估计值。u*和up为自适应滑模控制的两个部分，其中，u*包含非线性观测器的估计补偿，up包含自适应更新律。式(10)中滑模变量s(t)为：

(12)

(13)

式中：变量ε0,ε1,ε2为正常数，p0,p1,p2为常数。得到控制指令：

cosσ=uAda

(14)

由式(14)得到倾侧角的控制指令，通过式(12)给出的滑动面，在式(9)的控制器和式(13)自适应更新律共同作用下，最终系统(6)的状态x1,x2在原点邻域内收敛，也即实现，行星探测器的位置误差和速度误差能同时达到零。

注.闭环系统(6)利用自适应滑模控制算法可以收敛。然而，由于存在不确定性和扰动，控制输入会导致抖振，这是在工程实践中不希望看到的。文中采用非线性扰动观测器来估计总扰动，对控制输入进行补偿，能有效减少抖振和控制能耗。

3 仿真校验

针对火星大气进入段对所提出的方法进行仿真验证，仿真参数如表1所示。

表1 仿真参数Table 1 Simulation parameter

仿真结果如图2～图5所示。其中对高度、速度及扰动的实时观测估计如图2和图3所示。图2表示的是非线性观测器对总扰动的估计值、真实值及偏差。图3表示的是非线性观测器对高度、速度真实值、参考值及偏差。

图2 总扰动真实值、估计值及估计误差时间Fig.2 The total disturbance real value, estimated value and estimated error

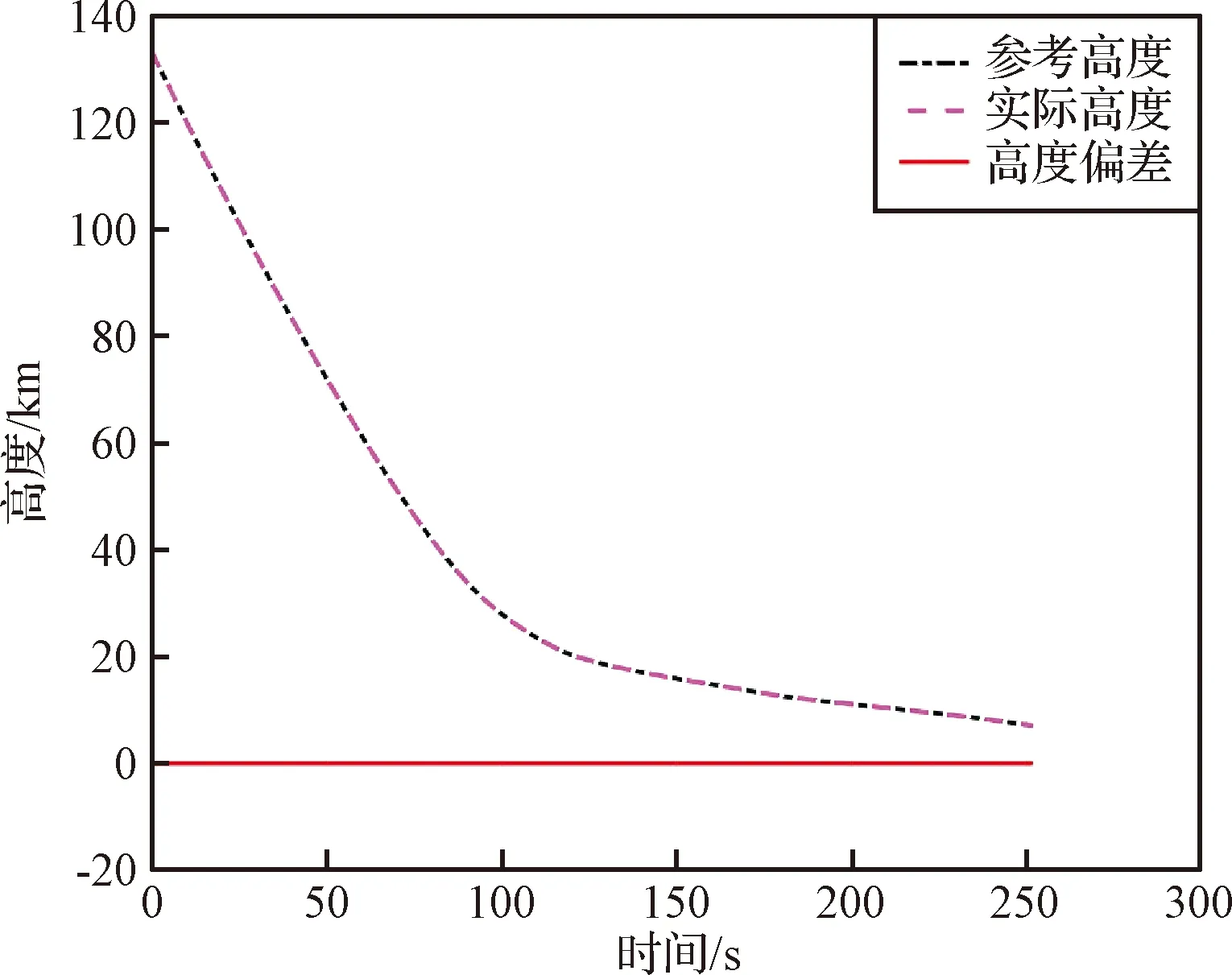
图3 高度真实值、参考值及偏差Fig.3 True value of altitude, speed, reference value and deviation

图4和图5为行星探测器开伞点的分布情况，图4为仅采用非奇异终端滑模时，开伞点的分布情况，图5为文中所提方法所对应的开伞点散布情况，即：采用自适应非奇异终端滑模，结合非线性观测器时。从仿真结果可以看出，采用文中所提出的方法，可以有效提高开伞点的精度，到达预定的开伞点，从而提高着陆任务的安全性。

仿真结果显示，非线性观测器能较好的跟踪状态，实现对探测器实时位置、速度及所受扰动的实时估计补偿。相比于仅采用自适应滑模控制的制导方法的控制精度和误差收敛速度有明显提高，能够对探测器的位置及速度进行实时估计，最终控制探测器精确到达预定开伞点。

图4 开伞点散布情况，仅采用非奇异终端滑模控制方法Fig.4 The dispersions of the final point, nonsingular terminal sliding mode control method

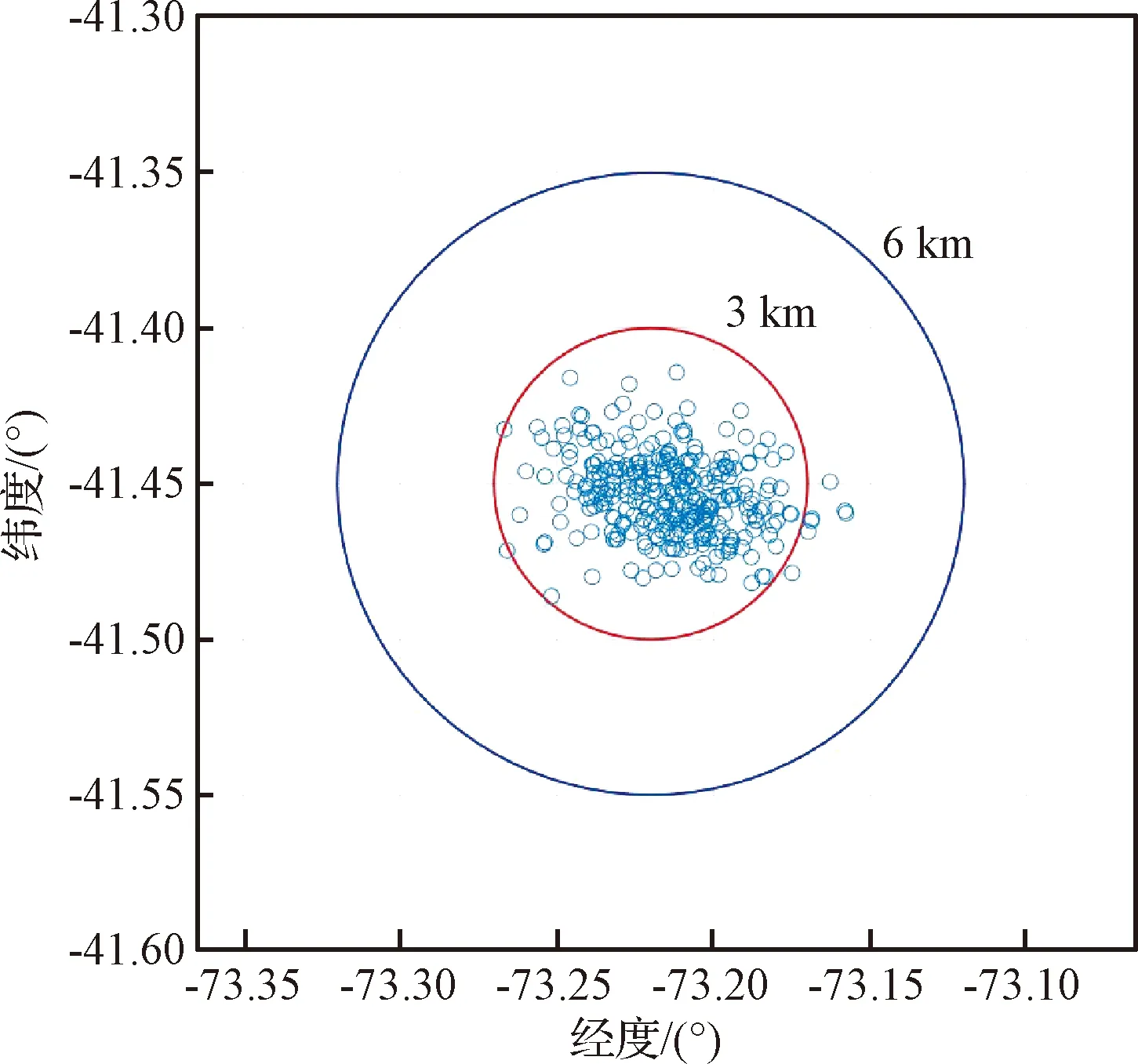
图5 开伞点散布情况，采用自适应终端滑模控制方法Fig.5 The dispersions of the final point, adaptive nonsingular terminal sliding mode control method

4 结 论

本文提出基于自适应滑模的行星着陆抗扰控制方法，通过将行星着陆问题转化为轨迹跟踪控制问题，采用自适应滑模控制方法实现探测器快速、精确跟踪参考轨迹。通过引入非线性观测器，有效估计与补偿总扰动。自适应滑模控制能快速将系统的状态控制到平衡点附近，具有减弱抖振，同时避免奇异性的特点。由于着陆过程存在干扰，结合非线性观测器对干扰进行精确估计补偿。最后，将该方法应用于火星着陆场景进行仿真，结果表面，提出的行星着陆控制方法能够在未知扰动存在的情况下有效实现扰动补偿，提高了着陆任务的安全性。