皮卫星星箭分离动力学模拟及其灵敏度分析

谢长雄，邓小雷，王建臣，林 欢

(1. 衢州学院机械工程学院，衢州 324000；2. 浙江理工大学机械与自动控制学院，杭州 310018；3. 浙江大学机械工程学院，杭州 310027)

0 引 言

皮卫星是基于微电子机械系统(Micro-electro-mechanical-systems,MEMS)的一种全新概念的微小卫星，它具有研发周期短、制造发射成本低、功能针对性强、载荷接口灵活等常规卫星无法比拟的优点。目前全世界从事皮卫星研制的机构已经超过100所，覆盖20多个国家[1]。

皮卫星体积小、重量轻，常规包带式星箭连接机构不能满足皮卫星星箭分离要求。早在20世纪90年代就有许多学者在研究皮卫星，但发现研究出来后找不到合适的星箭分离机构，大大延缓了皮卫星研究进程[2]。2000年2月7日两颗绳系皮卫星与“母”卫星OPAL分离进入太空，这标志着皮量级卫星时代的到来[3]。经过十来年的发展，国外主要有P-POD、XPOD、SPL、CSS、RAFT等型号皮卫星星箭分离机构[4-7]；国内，皮卫星星箭分离机构主要有浙江大学自主研发的“皮星一号A”、“皮星二号”星箭分离机构[8-9]和西北工业大学研制的“翱翔之星”星箭分离机构[10]。上述星箭分离机构都是针对立方星而开发，绝大多数均采用舱门解锁装置解锁、直线筒状导轨导向、单个分离弹簧分离的结构。

星箭分离事件是火箭飞行任务中的关键事件。分离物体不能与其他物体发生干涉，分离后卫星的入轨初始姿态决定卫星后续工作的顺利开展，星箭分离过程动力学分析得到了国内外相关学者关注。早在1966年，Palmer[11]在不考虑初始角速度的情况下，将星箭分离近似为平面相对运动，建立了星箭分离的数学模型，分析了弹簧刚度、星箭偏心质量等参数对分离过程的影响。Jeyakumar等[12]进一步考虑星箭初始角速度与重力梯度的影响，建立了星箭空间相对运动的数学模型，仿真模拟了星箭分离过程，并用概率统计方法分析了各设计参数的误差对入轨精度的扰动影响。付碧红等[13]对受到各种干扰力矩影响下的搭载星星箭分离过程进行了分析。上述分析均基于包带式多弹簧分离系统而展开。蒋超等[14]对筒式偏心在轨子卫星分离过程进行了分析，并考虑了卫星相对安装位置和分离弹簧弹性系数对分离姿态的影响，但并未考虑卫星与筒壁间的接触力、摩擦力等因素影响。此外，许多学者[15-17]对火箭分离机构参数、铰链结构、柔体动力学优化等问题也开展了较为详细的研究。

皮卫星通过体表太阳能电池片获得的能源有限，姿控能力弱，对星箭分离后入轨初始姿态要求较高。为了确保皮卫星入轨姿态在允许范围内，并为星箭分离机构的改进设计提供依据，本文基于自主研发的“皮星一号A”星箭分离机构，建立了包含该星箭分离机构与立方体皮卫星的星箭分离动力学模型，并考虑了皮卫星质心偏离量、分离弹簧及舱门扭簧弹性系数对分离姿态的影响，分析结果验证了设计参数选择的合理性。2010年9月22日， “皮星一号A”成功发射并下传了自带MEMS陀螺采集的入轨姿态数据，经分析发现，仿真分析结果与在轨分离数据较吻合。该模型对立方体皮纳卫星星箭分离机构的设计及星箭分离过程的分析具有很好的借鉴意义。

1 星箭分离过程简述

为保护主星安全，“皮星一号A”采用沿火箭径向分离方式。运载方在II、IV基准面上各提供一个安装平台用于皮卫星与星箭分离机构的安装(见图1)，这样的对称安装方式可保证在分离时分离冲量对运载姿态影响最小。

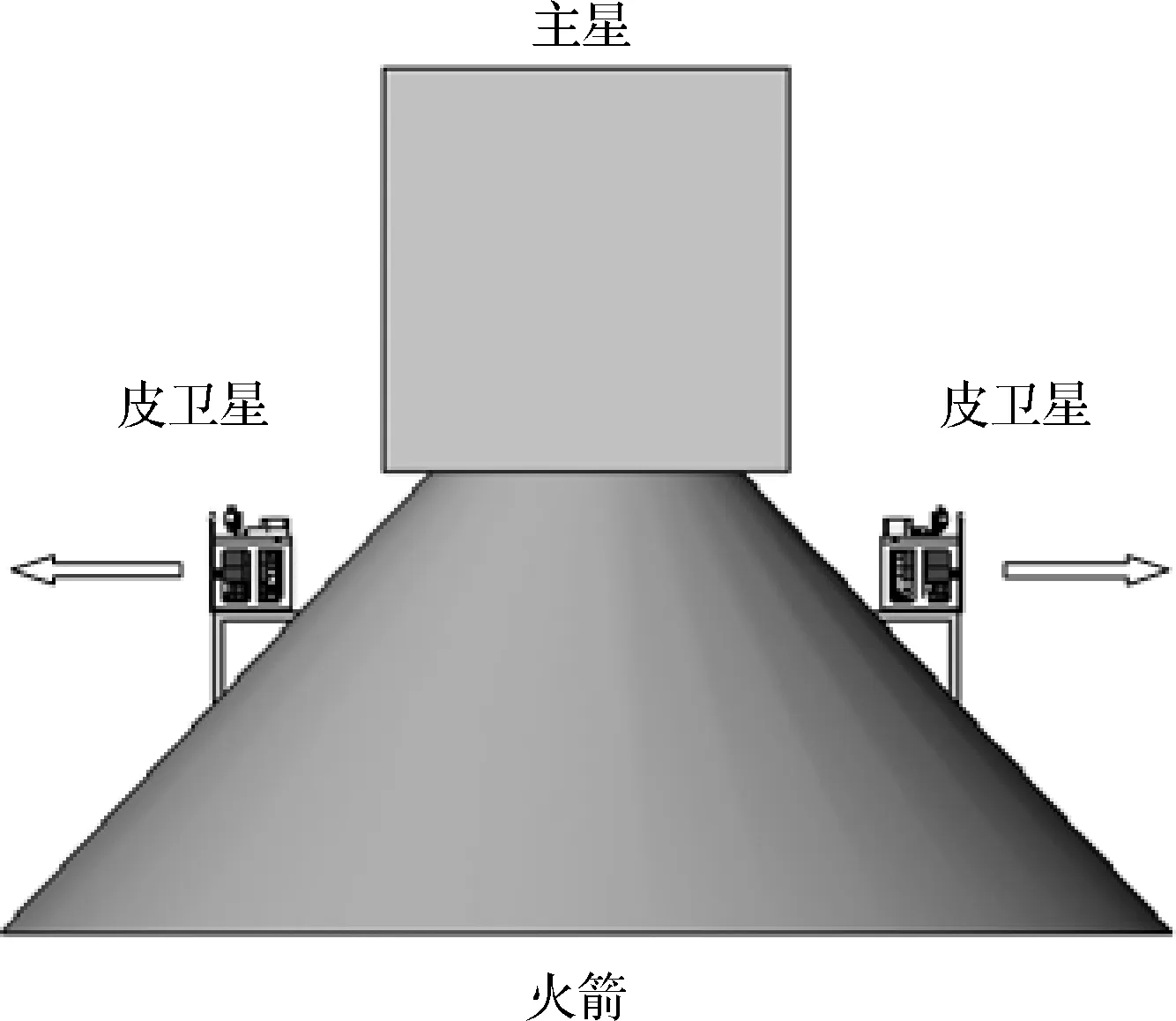
图1 皮卫星在火箭上安装关系示意图Fig.1 The assembly relationship between ‘ZDPS-1A’ picosatellite and rocket

星箭分离过程如图2所示，分离程序为：在星箭到达预定轨道后，由运载提供分离信号，火工器切断钛杆解锁，舱门在扭簧作用下打开，皮卫星在分离弹簧作用下沿着直线导轨向外滑出。整个星箭分离过程可分为三个阶段，第一阶段从舱门凸轮限制卫星运动到凸轮与卫星脱离接触时止，凸轮可以防止皮卫星与舱门干涉而影响入轨初始姿态；第二阶段，随着舱门打开速度越来越快，凸轮与卫星脱离接触，但皮卫星仍在筒状体内，在分离弹簧作用下继续分离，在舱门打开一定角度后，舱门弹簧锁销装置限制舱门来回摆动；第三阶段，皮卫星在弹簧作用下弹出筒状体，星箭完全分离。在整个分离过程中，为减少卫星与导轨间的摩擦，避免高空冷焊现象的发生，星箭分离机构导轨面经PTFE固体润滑处理。

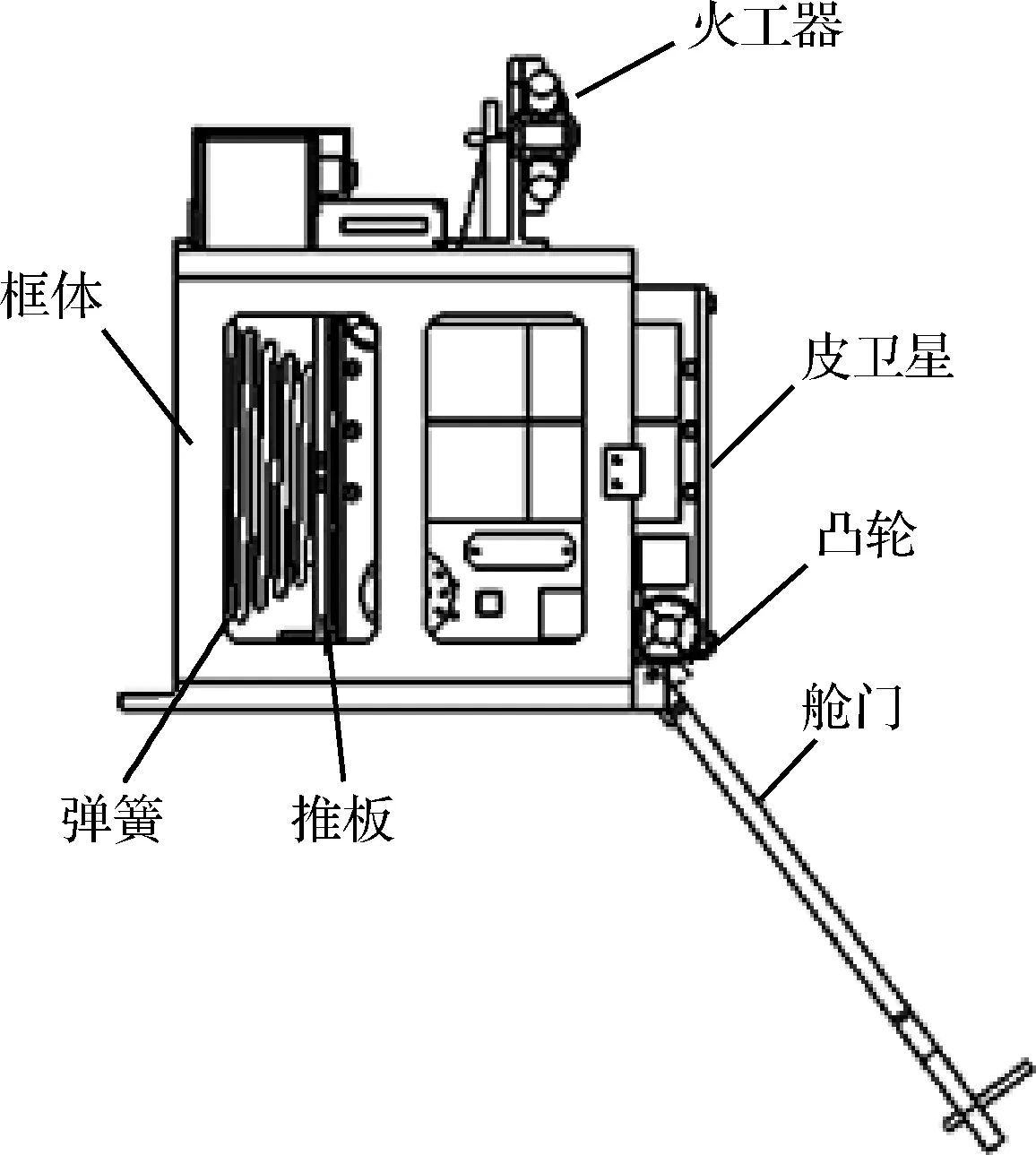
图2 星箭分离示意图Fig.2 The sketch of separation between ‘ZDPS-1A’ picosatellite and rocket

2 动力学分析与建模

2.1 数学建模

如图3所示，末级火箭为R，皮卫星为S1和S2，假定火箭末级与皮卫星均为刚体，在星箭分离前一瞬间火箭姿态为理想状态，无绕自身的飞行加速度和转动角速度。皮卫星为千克级卫星，而火箭末级重达数吨，且皮卫星采用左右对称同时分离方式，可假定星箭分离对火箭末级姿态无影响。

图3 相对坐标系和地心惯性坐标系Fig.3 Relative coordinates and geocentric inertial coordinates

2.1.1运动方程

根据刚体动力学动量定理、角动量定理有：

(1)

(2)

式中：m为皮卫星质量，v=vxiR+vyjR+vzkR为皮卫星分离速度，ω=riR+qjR+pkR为角速度，r,q,p分别为偏航角速度、俯仰角速度和翻转角速度，L=LxiR+LyjR+LzkR为角动量，Fext=FxiR+FyjR+FzkR为外力矢量，Mext=MxiR+MyjR+MzkR为外力矩矢量，iR,jR,kR为轨道坐标系各轴单位向量。角动量可由式(3)求得：

(3)

式中：Ixx,Iyy和Izz分别为绕偏航轴、俯仰轴、翻转轴的主惯性矩，Ixy,Ixz,Iyx,Iyz,Izx,Izy是关于指定平面的惯性积。

2.1.2外力分析

在星箭分离过程中，皮卫星除受分离弹簧力的作用外，还受到地球引力、接触力、摩擦力以及轨道摄动力的作用。因轨道摄动力很小，与其他力相比可以忽略其影响。本文主要考虑在分离弹簧力、舱门扭簧力、地球引力、皮卫星与分离机构各元件之间的接触力及摩擦力影响下的入轨初始姿态动力学问题。

1)弹簧力

圆锥螺旋弹簧具有压缩后整体尺寸小、不易发生共振等优点，故选取圆锥弹簧作为星箭分离机构的分离弹簧，弹簧自由长度与导轨长度相当。因圆锥弹簧本身横向稳定性好，且通过弹簧座与框体、推板相连，故在仿真计算中不考虑圆锥弹簧横向分力，并假定圆锥弹簧无装配误差，弹簧力作用线与皮卫星中轴线重合。

圆锥弹簧弹性系数并不恒定，在受到压并力作用时，弹簧第一圈未压并前弹性系数为常数，当第一圈压并后，圆锥弹簧作用力与变形近似抛物线关系。其关系曲线如图4所示。

图4 圆锥弹簧载荷与变形关系曲线Fig.4 The relation between deformation and load of the conical spring

2)扭簧力

在分离过程中，由扭簧为舱门打开提供扭矩。扭簧弹性系数为9.06×10-3Nm/(°)。舱门在锁紧状态时扭簧预紧角度为180°。

3)接触力

研究多刚体中的接触碰撞问题一般有两类方法：恢复系数方法和等效弹簧阻尼方法。相比恢复系数方法，等效阻尼方法将碰撞过程中接触力等效成一个弹簧阻尼模型，可以较真实地模拟出接触碰撞过程[18]。

接触力计算公式如下：

(4)

4)重力

在轨道环境中，地球引力为皮卫星绕地球转动提供了向心力的作用，但因有其他星球引力的作用，皮卫星并未处于完全失重状态。航天器在轨道运行过程中具有约10-6g大小的重力加速度。重力方向垂直于星箭分离机构侧面。

5)摩擦力

为防止皮卫星与导轨面因摩擦力过大或冷焊导致分离失败，在卫星与导轨接触面采用镀金处理，导轨面采用PTFE固体润滑处理。与大气环境相比，PTFE固体润滑层在太空环境下的摩擦系数会有所变化，因复合环境试验很难实现，只能对该材料进行单一环境试验以观察单一环境条件下该材料摩擦系数的变化。对该材料进行单一环境试验后发现，PTFE在大气环境中该材料摩擦系数仅为0.02，真空环境下的摩擦系数为0.1，而在经原子氧和紫外线辐照后PTFE材料的摩擦系数将增大到0.15。

图2和图3中，横轴表示冲击作用的滞后期间数(单位：月度)，纵轴分别表示股价增长率的变化和投资者情绪增长率的变化，实线表示脉冲效应函数，虚线表示正负两倍标准差偏离带。

2.2 仿真建模

皮卫星和星箭分离机构结构复杂，需要精密装配，这依靠ADAMS自带的建模工具很难完成，故选用SOLIDWORKS建立整个卫星和星箭分离机构的实体模型，然后将实体模型导入ADAMS中。在定义完各物体的物理属性后，对皮卫星及星箭分离机构各零部件根据实际运动情况采用布尔运算合并成几个整体，整个模型合并为皮卫星、框体、舱门和推板共四个刚体，各个刚体物理属性与实物一致。在框体与大地之间创建固定副，舱门与框体之间创建转动副。舱门上设置扭簧力，在框体与推板之间采用弹簧连接，因弹簧刚度不恒定，采用样条曲线来模拟弹簧推力，推板与导轨、推板与星体、星体与导轨、星体与舱门之间设置接触力与摩擦力，并设置在轨环境下的重力大小与方向。虚拟样机模型见图5。

图5 皮卫星及星箭分离机构虚拟样机模型Fig.5 The virtual prototype model of ‘ZDPS-1A’ picosatellite and its separation mechanism

3 参数灵敏度分析

皮卫星姿控能力有限，在星箭分离过程中，除皮卫星与运载在分离时不能发生干涉碰撞的要求外，姿控分系统对皮卫星入轨初始姿态也提出了相关要求，具体如表1所示。

表1 皮卫星星箭分离机构技术指标Table 1 Technical indices of the separation mechanism

为合理设计星箭分离机构，需评估皮卫星质心偏心量、分离弹簧与舱门扭簧弹性系数等关键参数对皮卫星分离姿态的影响，基于上述仿真模型，利用参数化点和建立设计变量的方式建立了皮卫星星箭分离参数化模型。建立的设计变量见表2，其中除了质心偏心量外，其余均值均为设计值或实测值。

表2 设计变量Table 2 Design variables

3.1 质心偏心量的影响

如图6～9所示，质心偏心量对分离速度、滚动角速度变化影响较小，对偏航角速度和俯仰角速度影响较大。当偏心量达到极限状态时，偏航角速度均超出姿控分系统对皮卫星角速度偏差要求。当偏心量为(0.5,0.5,0.5)时，俯仰角速度达到3.12(°)/s；当偏心量为(-0.5,-0.5,-0.5)时，俯仰角速度达到-3.15(°)/s；而当质心偏心量为(0,0,0)时，偏航角速度和俯仰角速度因受凸轮不对中影响，分别为-0.43(°)/s和-0.28(°)/s，均在表1所示技术指标范围内。

图6 皮卫星弹射速度随质心偏心量变化关系Fig.6 Effect of eccentricity on the separation speed

图7 皮卫星滚动角速度随质心偏心量变化关系Fig.7 Effect of eccentricity on the roll angle rates

图9 皮卫星俯仰角速度随质心偏心量变化关系Fig.9 Effect of eccentricity on the pitch angle rates

3.2 分离弹簧弹性系数的影响

图10 皮卫星弹射速度随分离弹簧弹性系数变化关系Fig.10 Effect of separation spring elasticity coefficient on the separation speed

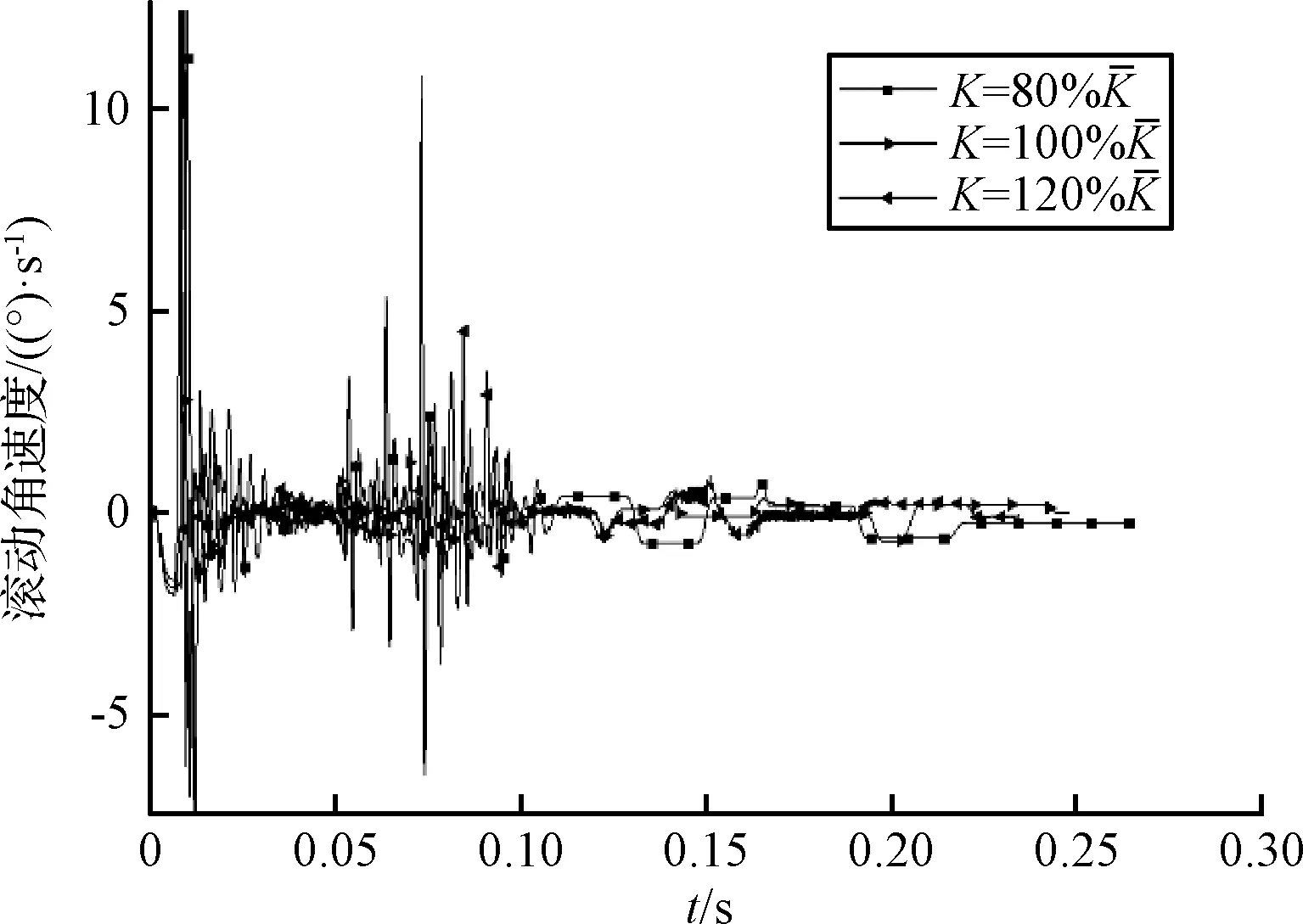
图11 皮卫星滚动角速度随分离弹簧弹性系数变化关系Fig.11 Effect of separation spring elasticity coefficient on the roll angle rates

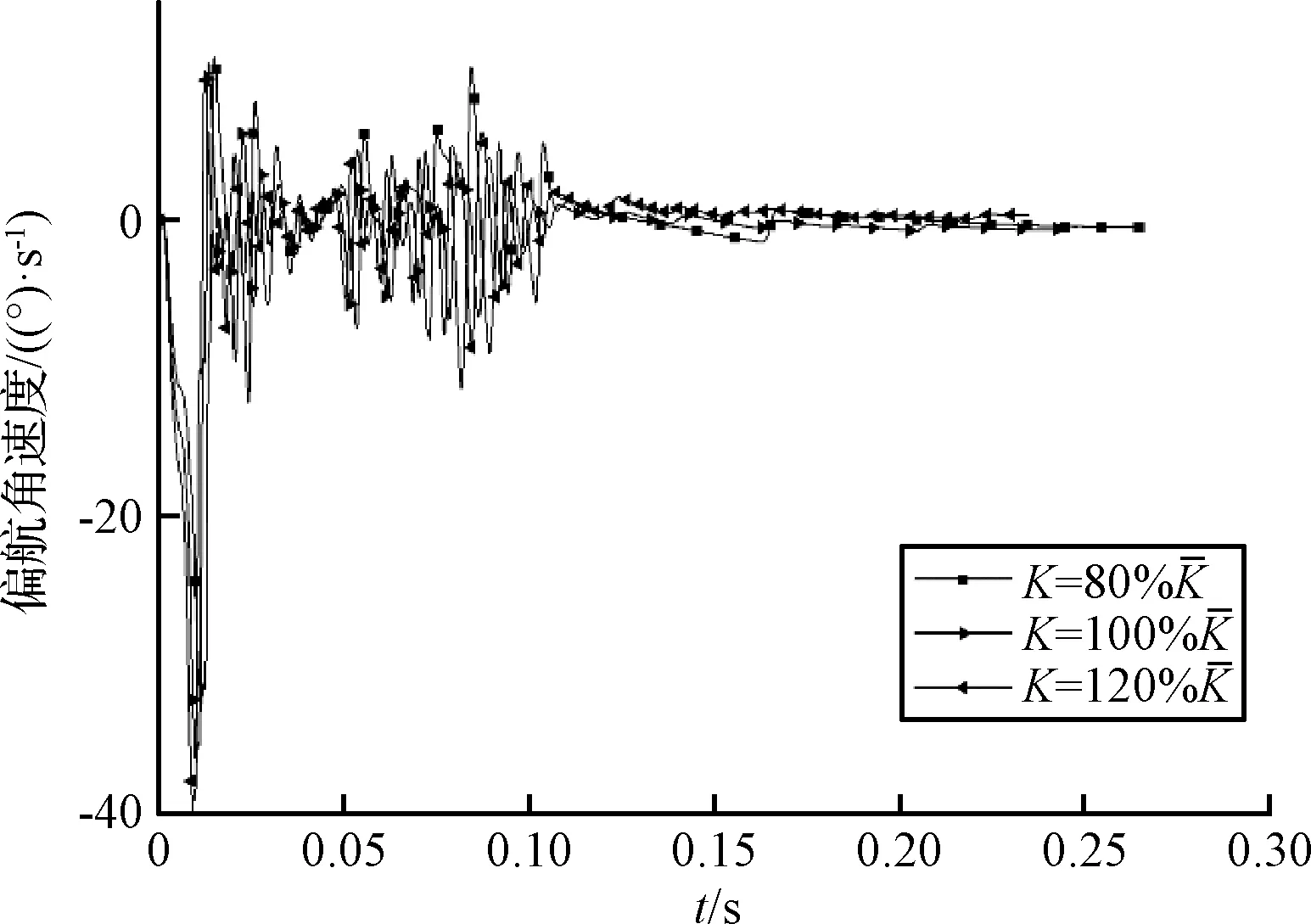
图12 皮卫星偏航角速度随分离弹簧弹性系数变化关系Fig.12 Effect of separation spring elasticity coefficient on the yaw angle rates

图13 皮卫星俯仰角速度随分离弹簧弹性系数变化关系Fig.13 Effect of separation spring elasticity coefficient on the pitch angle rates

图14 皮卫星弹射速度随舱门扭簧弹性系数变化关系Fig.14 Effect of torsion spring elasticity coefficient on the separation speed

这主要是因为凸轮机构与卫星接触部分位于卫星前表面下边缘且并不对中，在星箭分离过程中产生了一定的偏置力矩。当分离弹簧弹性系数变大时，在分离前期，凸轮与皮卫星下边缘的接触力较大；在分离后期，由于舱门打开速度变快使得凸轮与皮卫星接触力慢慢变小。而星箭分离前期卫星绝大部分尚在导轨内，导轨纠偏作用较明显，随着卫星的分离，导轨纠偏作用越来越弱。这导致了随着分离弹簧弹性系数变小而分离角速度增大这一现象的发生。

3.3 舱门扭簧弹性系数的影响

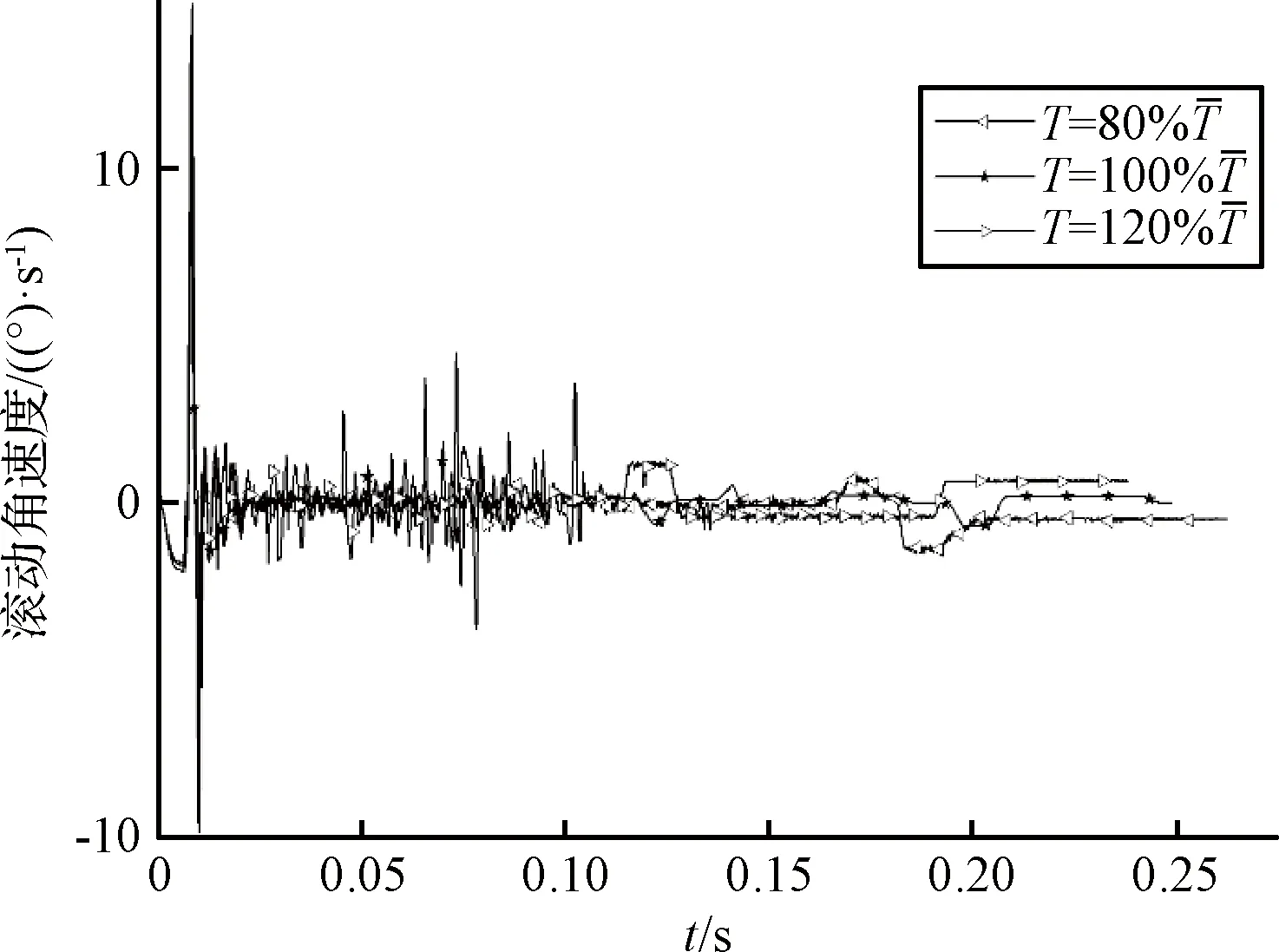
图15 皮卫星滚动角速度随舱门扭簧弹性系数变化关系Fig.15 Effect of torsion spring elasticity coefficient on the roll angle rates

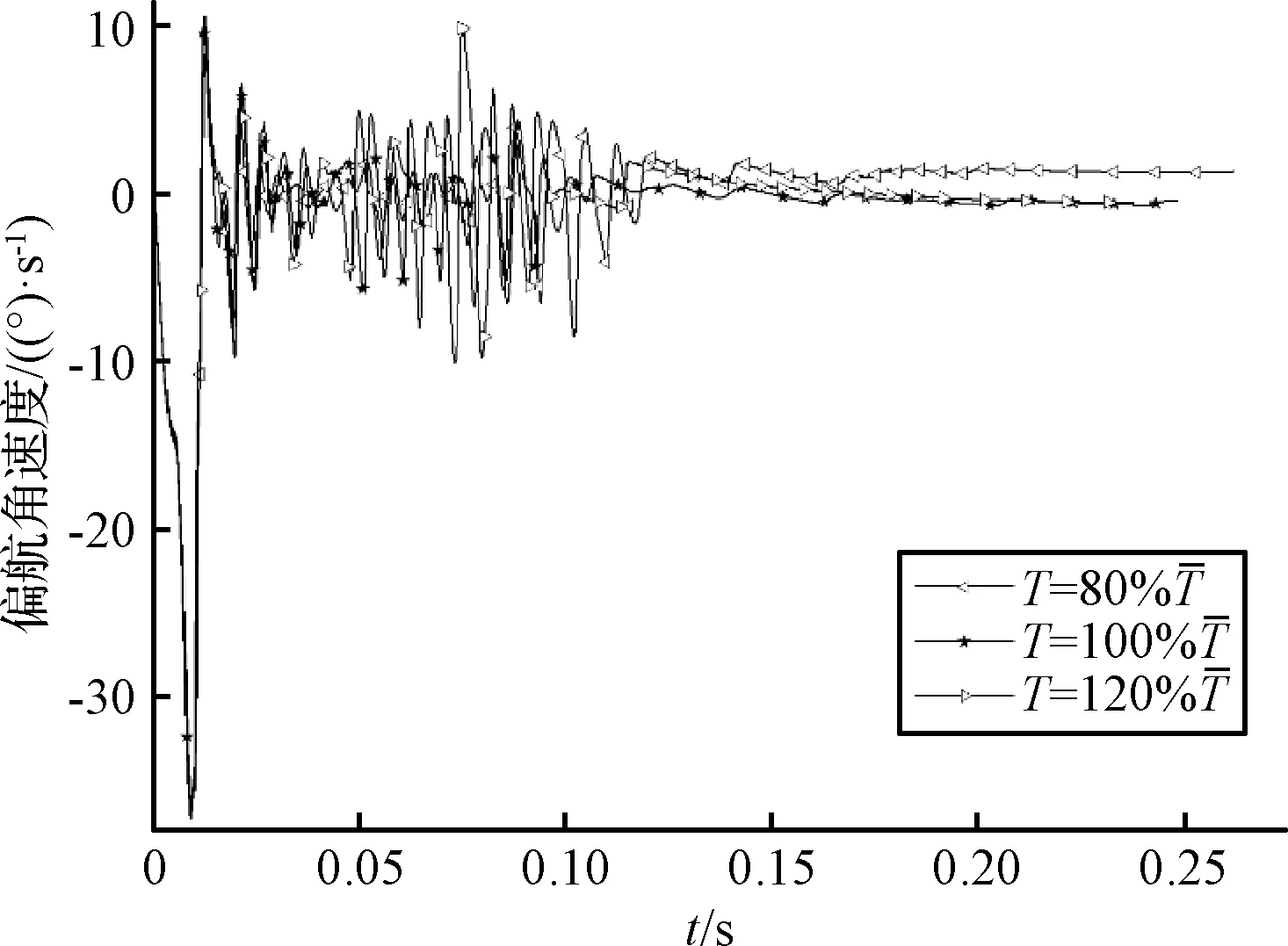
图16 皮卫星偏航角速度随舱门扭簧弹性系数变化关系Fig.16 Effect of torsion spring elasticity coefficient on the yaw angle rates

图17 皮卫星俯仰角速度随舱门扭簧弹性系数变化关系Fig.17 Effect of torsion spring elasticity coefficient on the pitch angle rates

在舱门扭簧弹性系数较小时，因舱门打开速度较慢，故舱门上凸轮与卫星下边缘接触力变大，所以卫星在分离过程中，偏航角速度和俯仰角速度出现了较大的振荡，这使得皮卫星分离角速度变大。当舱门扭簧弹性系数较大时，由于舱门打开速度过快，星箭分离时间缩短，致使导轨纠偏作用时间缩短，故皮卫星分离角速度也有一定程度的增大趋势。

从图6～图17可以看出，虽然各参数对卫星分离姿态的影响有一定耦合性，但不难得出各参数对分离姿态的影响规律：卫星偏心量对分离姿态影响最大，当卫星偏心量大于0.5 mm时，俯仰角速度和偏航角速度将超过3(°)/s，不再满足姿控分系统要求；分离弹簧和舱门扭簧弹性系数对分离姿态影响次之，因为舱门扭簧弹性系数是根据分离弹簧弹性系数而设计的，当在设计值附近变化时，分离姿态均有变坏的趋势。

3.4 星箭分离安全性分析

质心偏心量对卫星弹射分离速度并无明显影响(见图6)；舱门扭簧弹性系数对卫星分离时间影响较为明显，但对卫星分离速度影响较少(见图14)；分离弹簧弹性系数对卫星分离速度影响较大，当分离弹簧弹性系数为设计值的80%时，卫星分离速度为1.17 m/s，当其为设计值时，卫星分离速度为1.31 m/s，而当其为设计值的120%时，卫星分离速度为1.46 m/s(见图10)，均在表1所规定的分离速度性能指标范围内。

在星箭分离过程中，还需考虑卫星分离及舱门打开过程中的干涉问题。卫星与舱门的干涉不仅会影响到卫星初始入轨姿态，同时还可能损坏卫星体表的太阳能电池片。在此对分离弹簧弹性系数为设计值的120%，舱门扭簧弹性系数为设计值的80%时的极端工况下星箭分离干涉问题展开分析。在凸轮与卫星脱离接触时刻，卫星分离距离为15.63 mm，卫星与导轨间隙仅0.5 mm，而卫星边长为150 mm，在此不考虑卫星角度变化影响。

分析结果如图18所示，在分离前期，凸轮限位点与卫星前边缘一直处于接触状态。当t=0.108 s时，限位点速度超过卫星分离速度，凸轮限位机构与皮卫星前边缘脱离。当卫星前边缘在分离方向上追上凸轮时，舱门打开角度为137.45°，此时凸轮最高点距卫星下表面为1.12 mm，而体表太阳能电池片厚度仅0.5 mm，故在极端工况下星箭分离是安全的，参数取值范围是合理可行的。

图18 凸轮限位点位置及皮卫星弹射距离随时间变化关系Fig.18 The curves of cam limit point position and picosatellite separation distances

4 试验分析

在试验过程中，分离弹簧和舱门扭簧弹性系数为设计值，卫星经配重后质心偏心量为(0.12,-0.29,0.48)。2010年9月22日，“皮星一号A”成功发射，随后，地面接收到皮卫星下传的分离时间及MEMS陀螺采集到的各方向的角速率，试验结果与仿真结果对比如表3所示。从表3可以看出，仿真结果与实际分离结果基本相符，皮卫星入轨姿态可满足姿控分系统要求。

图19为皮卫星在轨拍摄的地球照片，照片清晰无重影，说明卫星入轨初始姿态在姿控分系统可控范围内，为卫星后续工作提供了一个良好开端。

图19 卫星在轨拍摄的地球照片Fig.19 Picture of the Earth taking by on-orbit picosatellite

5 结束语

皮卫星入轨初始姿态对皮卫星姿控及后续工作的开展具有较大影响。本文针对自主研发的皮卫星星箭分离机构展开了理论研究，建立了皮卫星星箭分离模型，并通过多体动力学仿真得出了皮卫星及其星箭分离机构相关参数对分离姿态的影响规律。

1)皮卫星偏心量是影响分离姿态的关键因素，过大的偏心量将给皮卫星姿控系统带来较大压力，故需对皮卫星进行严格的质心配平设计。

2)分离弹簧和舱门扭簧弹性系数对卫星分离姿态影响次之，但合理配置分离弹簧和舱门扭簧弹性系数有利于卫星以较好的姿态分离。

3)经理论与仿真分析及试验验证，该机构可满足相关技术指标要求，能圆满完成星箭分离任务。为皮卫星后续工作的顺利进行提供了保障。