圆柱形扭簧簧圈椭圆度对应力及刚度的影响

姜旭涛，黄志辉，穆云飞

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

某用于钢琴踏板的圆柱螺旋扭转弹簧(以下简称扭簧)，通过钢琴踏板活动，在变载荷应力下工作50万次后发生疲劳破坏，与设计要求的疲劳寿命N≥100万次差异较大。因此，对扭簧实物进行检查后发现扭簧簧圈制成了椭圆形，而非标准圆形。为探究扭簧簧圈椭圆度对扭簧部分力学性能的影响，本文就簧圈椭圆度对扭簧所受应力及刚度的影响进行研究与分析。

1 标准簧圈扭簧部分力学性能理论计算

1.1 扭簧研究模型介绍

该扭簧顺旋向扭转，使用SWP-B琴钢丝材料，总圈数n=5.21，初始夹角φ0=104.4°，材料直径d=3.8mm，内径D1=16mm，固定侧扭臂l1=66mm，施力侧扭臂l2=45mm，自由高度H=33.29mm，安装转矩T1=4599.20N·mm，工作转矩T2=6 713.87N·mm。

在CATIA中建立扭簧三维模型时，通过高度h=H-d=33.29-3.8=29.49mm以及转数n=5.21来定义螺旋曲线；将螺旋曲线与两扭臂l1、l2接合并将其作为中心曲线，将d=3.8mm的圆作为轮廓，定义肋，得到标准簧圈扭簧的三维模型如图1所示。

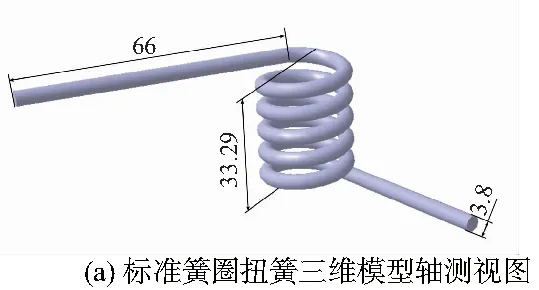
图1 标准簧圈扭簧三维模型

1.2 扭簧弯曲应力计算

根据GB/T 23935—2009《圆柱螺旋弹簧设计计算》[1]，该扭簧所受弯曲应力的计算公式为

(1)

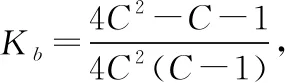
将安装转矩T1与工作转矩T2分别代入公式(1)中，得：

该扭簧所受最小弯曲应力

所受最大弯曲应力

1.3 扭簧疲劳极限分析

扭簧在应力循环中的循环特征的计算公式为

(2)

则该扭簧的循环特征

查得当材料直径d=3.8mm时，SWP-B琴钢丝的抗拉强度Rm为1810～1960MPa[2]，取Rm=1810MPa，则该扭簧的上限应力系数

根据扭转弹簧疲劳极限图(图2)判定规则：若循环特征γ与上限应力系数Q的交点在图中应力循环10n下方，说明该扭簧的疲劳强度N>10n次。

图2 扭转弹簧疲劳极限图

在图2中，该扭簧循环特征γ与上限应力系数Q的交点在图中107下方，理论上疲劳寿命N>107次[3]。

2 标准簧圈扭簧有限元计算

本文通过在CATIA建立扭簧三维模型，将扭簧模型以stp格式导入HyperMesh进行网格划分、赋予材料属性、设置单元属性、建立接触、施加载荷及边界条件，然后输出cdb模型，将其导入ANSYS进行计算[4-5]。

2.1 扭簧有限元模型建立

根据扭簧实际工作情况，将扭簧三维模型导入HyperMesh后，建立与扭簧接触处间隙为0的销轴。

两者都采用SWP-B琴钢丝材料，SWP-B琴钢丝的材料属性如表1所示。

表1 SWP-B琴钢丝材料属性

根据扭簧实际工作情况，扭簧与销轴之间存在接触，所以需要对接触部分进行非线性接触设置，设置销轴表面为目标面，扭簧表面为接触面 。

根据扭簧实际工作情况，l1=66mm端为固定侧扭臂，l2=45mm端为施力侧扭臂。在扭簧工作时，固定侧扭臂只在轴向发生位移，而施力侧扭臂由于受转矩T的作用，只在轴向和转矩方向发生位移，销轴在扭簧工作期间为固定的。对于固定侧扭臂，需在扭臂端面建立一空间直角坐标系，然后将固定侧扭臂上需要约束的节点分配给该局部坐标系，约束固定侧扭臂节点Ux和Uy自由度；对于施力侧扭臂，在全局坐标系中约束其Uz自由度；对于销轴，在全局坐标系中约束其上、下端面的Ux、Uy和Uz自由度。

在有限元模型中，对扭簧转矩的施加要转化成力乘以力臂，公式为

T=FR

(3)

式中：F为施加在扭臂的力，N；R为力臂，mm[6]。

扭簧的工作转矩T2=6 713.87N·mm，取力臂R1=33.75mm，由公式(3)得施加在扭臂的力为

采用mass质量单元与rbe3刚性单元，将扭簧施力侧扭臂的受力节点耦合为一个受力节点。由于无法对耦合后的节点直接施加垂直于扭臂的载荷，所以需要在扭簧销轴的中心位置建立空间柱坐标系，然后将力F沿柱坐标系分解为F1=50.72N，-F2=192.35N，将其施加在耦合的受力节点上。

HyperMesh处理后的标准簧圈扭簧有限元模型如图3所示。

图3 标准簧圈扭簧有限元模型

2.2 扭簧有限元模型计算结果

将HyperMesh处理的有限元模型导入ANSYS进行求解。扭簧Von-Mises等效应力云图如图4所示。

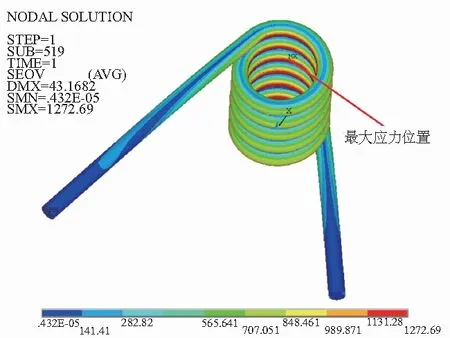
图4 标准簧圈扭簧Von-Mises等效应力云图

由有限元计算结果可知，扭簧所受最大应力为1272.69MPa，位于扭簧内圈扭转处。经测量，扭簧扭转变形角φ1=56°。根据现代机械设计手册[7]，扭转刚度与扭转角的关系式为

(4)

将扭转变形角代入公式(4)可得有限元计算的扭转刚度为

3 椭圆簧圈扭簧有限元计算

在弹簧成型过程中，由于工装及加工的原因，使得簧圈成了椭圆，且每个弹簧的椭圆度都不一致。本文采取等距取样的原则，以0.5mm为抽样距离进行簧圈椭圆度的取值，首先选取簧圈椭圆度e为0.5mm、1.0mm、1.5mm的扭簧并对其进行有限元计算。将有限元计算结果进行分析拟合，得到簧圈椭圆度与扭簧所受最大应力呈线性关系的结论。为了验证结论的准确性，选取簧圈椭圆度e为3.0mm的扭簧进行有限元计算。

椭圆簧圈扭簧三维模型如图5所示。

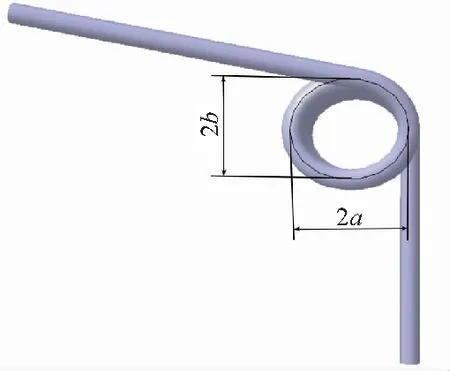
图5 椭圆簧圈扭簧三维模型

3.1 椭圆簧圈扭簧三维模型建立

在椭圆中，椭圆度与椭圆长、短轴的关系式为

e=2a-2b

(5)

式中：e为椭圆度，mm；a为椭圆长半轴，mm；b为椭圆短半轴，mm。

椭圆周长公式为

C1=2πb+4(a-b)

(6)

构造椭圆簧圈扭簧时，需保证椭圆簧圈与标准簧圈周长相同，即

2πb+4(a-b)=πD

(7)

将4组椭圆度e分别代入公式(5)中，并与公式(7)联立，得到各组椭圆簧圈的参数如表2所示。

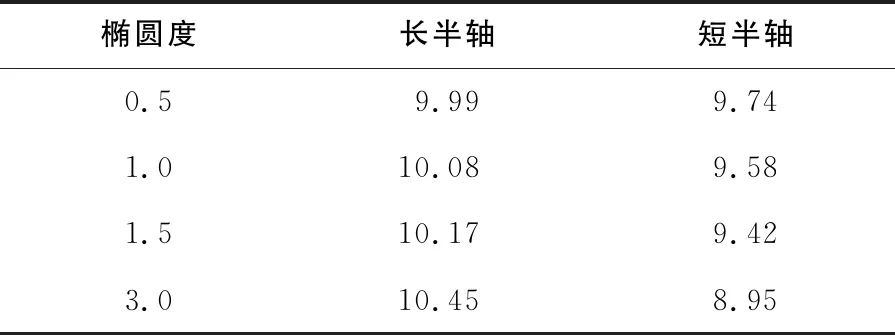
表2 椭圆簧圈参数 单位：mm

利用计算所得参数在CATIA中分别构造对应椭圆度的椭圆簧圈扭簧。

3.2 椭圆簧圈扭簧有限元模型建立

采用与2.2中标准簧圈扭簧有限元模型相同的方式分别对各组椭圆簧圈扭簧进行网格划分，单元、材料、接触设置及约束和载荷的施加。

3.3 椭圆簧圈扭簧有限元模型计算结果

将HyperMesh处理的有限元模型导入ANSYS进行求解。各组椭圆簧圈扭簧Von-Mises等效应力云图分别如图6-图9所示。

图6 0.5mm椭圆度扭簧Von-Mises等效应力云图

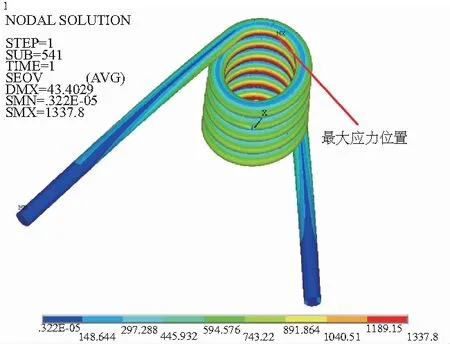
图7 1.0mm椭圆度扭簧Von-Mises等效应力云图

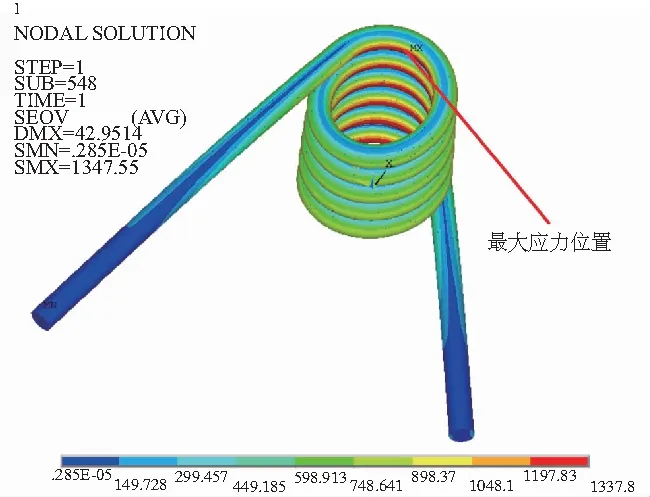
图8 1.5mm椭圆度扭簧Von-Mises等效应力云图

图9 3.0mm椭圆度扭簧Von-Mises等效应力云图

整理得各组扭簧有限元计算结果如表3所示。

表3 各组扭簧有限元计算结果

4 有限元计算结果分析

4.1 簧圈椭圆度对刚度的影响

由表3可知，扭簧刚度不随簧圈椭圆度的变化而变化，即簧圈椭圆度对扭簧刚度没有影响。

4.2 簧圈椭圆度对应力的影响

以簧圈椭圆度e为横轴，以应力σ为纵轴，将表3中各组椭圆度所对应的应力值进行拟合，得到拟合曲线σ=24.72e+1312.85(e>0)，如图10所示。

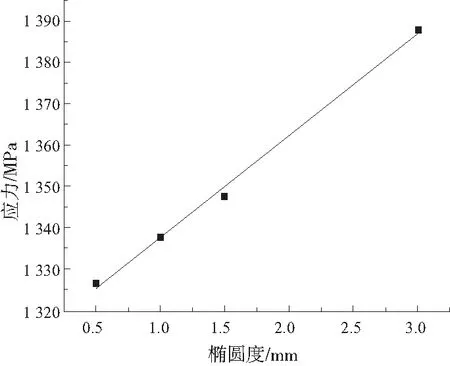
图10 簧圈椭圆度与所受最大应力关系拟合曲线

5 结语

1)扭簧簧圈椭圆度对扭簧的刚度没有影响。

2)扭簧所受最大应力随扭簧簧圈椭圆度的增大而增大，且两者呈线性关系；在本文选取的模型中，扭簧椭圆度与所受最大应力的线性关系式为σ=24.72e+1312.85(e>0)。