包带约束下的星箭连接环组合力学分析

陈夜,王开浚,虞自飞,张如变,王志国

(上海卫星工程研究所,上海 201109)

0 引言

包带连接是目前广泛采用的星箭连接方式。包带连接机构一般包括包带、卡块、分离弹簧、爆炸螺栓等。在卫星发射阶段,包带连接机构夹紧星箭连接环与火箭适配器;入轨后,包带在火工品等分离装置作用下解锁,实现星箭分离。包带约束以接触力的形式传递到星箭连接环上,形成压力与摩擦力,对星箭连接环的应力与变形有着不可忽视的影响。

工程上,由于涉及复杂的非线性接触问题,星箭连接环的力学分析通常忽略包带约束的影响,仅考虑发射过载以简化分析,导致仿真分析不能完全覆盖实际工况。近年来,随着相关理论与计算机水平的发展,国内外对包带连接的动力学特性、强度与冲击特性开展了一定的研究。白绍竣[1]详细研究了包带连接的接触力学特性,推导了包带模型的有限元列式,并通过试验发现了包带连接系统的软刚度特性;ROME等[2]采用对称有限元模型分析了包带连接部件之间的接触力以及预紧力;西班牙航空制造有限公司(CASA)[3]研究了包带承载能力的影响因素以及提升方法;瑞典 SAAB 航天公司成功研制了用于10 000 kg重型卫星的包带连接结构[4]。韩晓健等[5]通过试验研究了包带预紧力、起爆器、装药量等因素对包带分离冲击响应的影响。

上述相关研究主要聚焦于包带连接系统的力学特性,并未综合考虑发射过载的影响。本文从实际工程背景出发,将星箭连接环的力学环境等效为包带接触力与发射过载的组合作用,包含了线性与非线性的力学行为,通过建立详细有限元模型,分析得到星箭连接环的应力与变形,为某型星箭连接环的标准化、型谱化推广提供参考与依据。

1 星箭连接环力学环境分析

1.1 包带接触作用

图1所示为包带连接机构的接触关系图。卡块通过螺钉固定在包带上,包带的预紧力对卡块形成向内的压力,高刚度的卡块通过楔形槽将压力传递给星箭连接环与适配器,实现对星箭接口的压紧。

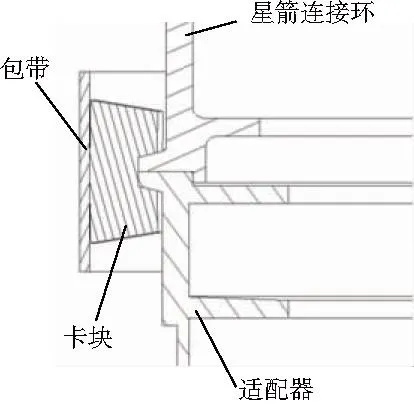
图1 接触关系剖视图

卡块是传递接触力的关键部件,每个卡块上存在3个接触关系,即包带内表面与卡块外表面、卡块楔形槽与星箭连接环斜面、卡块楔形槽与适配器斜面的接触。为防止尺寸之间的干涉,星箭连接环、适配器的外缘与卡块不接触。

以星箭连接环为研究对象,连接环与卡块、适配器接触面的受力状态如图2所示。其中,卡块接触面是主传力面,面上存在法向压力fn1与切向摩擦力τn1;适配器接触面形状为阶梯型,面上力由接触面的限位作用引发,力的方向以法向接触力fn2、fn3为主,可以忽略切向摩擦力。由于接触力的大小取决于是否接触以及接触的深度,而接触区域又随着包带预紧力的增大而变化,所以接触力具有很强的非线性特性。

图2 星箭连接环接触力

考虑接触力的星箭连接环静力平衡方程为

(1)

式中:K为刚度阵;u为位移,P为外载荷,下标n、i分别表示非接触界面区域和接触界面区域;F、τ分别为接触表面压力与摩擦力,在预紧力的加载过程中,F、τ是变量。式(1)是与过程相关的多变量耦合方程,几乎不存在解析解。为此,ABAQUS有限元软件通过数值解法求解接触非线性问题,将加载过程分为若干微小的载荷步,每一载荷步进行接触判断与动量平衡计算,采用迭代算法求解结构的响应。

接触分析除了要满足常规静力分析的平衡条件外,还增加了两个假设:1)接触面上物体必须满足不可侵彻性条件,面力必须满足动量平衡;2)接触面的法向面力只能为压力。

1.2 发射过载

发射过载实质是卫星发射加速度产生的惯性力,卫星质心处的加速度分量包括纵向加速度al和横向加速度aw,纵向为火箭轴向。星箭连接环承载了卫星的全部过载,纵向过载在星箭连接环上产生压力Fl,横向过载则产生弯矩Mw与剪力Fw。

压力Fl、弯矩Mw、剪力Fw与卫星质心加速度al、aw有如下关系:

Fl=mal,Fw=maw,Mw=mhaw

(2)

式中:m表示卫星质量;h为质心高度。发射过载的力学特性是线性的。

1.3 组合力学分析方案

不论是非线性的接触分析,还是线性的过载分析,商业有限元软件均具备相应的求解模块。但若考虑二者的组合作用,将进一步增大非线性迭代过程的复杂性,造成分析过程难以收敛。

为此,本文将组合力学过程在时序上分步考虑,即先开展包带接触的非线性分析,以接触分析的结果为基础,固化接触状态再进行线性过载分析,最后将两次分析得到的应力场、位移场线性叠加,得出最终分析结果。分析方案如图3所示。

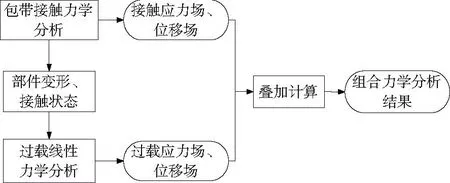
图3 组合力学分析方案

2 有限元建模

2.1 有限元模型

卫星发射段的过载力全部通过承力筒传递到星箭连接环,所以对星箭连接环而言,卫星可等效为一个固定连接在承力筒上的集中质量点。在ABAQUS有限元分析软件中建立卫星承力筒、包带、卡块、适配器、星箭连接环的有限元模型,如图4所示。其中,包带连接机构分为3段,每段上固定连接有若干卡块。星箭连接环采用一阶减缩积分体单元C3D8R建模,模型中详细反映了对接面的几何形状,以保证接触分析的准确性。星箭连接环剖视图如图5所示。

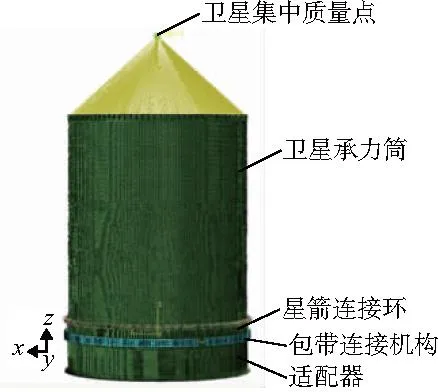
图4 有限元分析模型

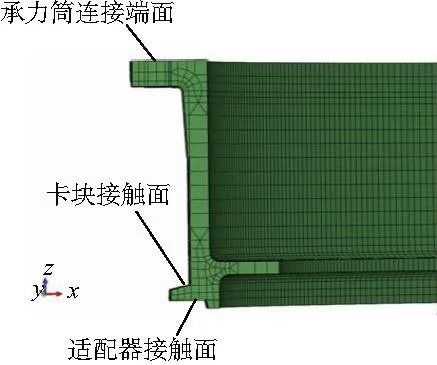
图5 星箭连接环有限元模型

2.2 接触关系定义

考虑到星箭连接环、包带、适配器之间的接触关系,在有限元模型中定义4种接触对,接触面的特性如表1所示。

表1 接触关系特性表

2.3 分析步设定

依据图3的分析方案,定义包带接触力学分析与过载线性力学分析两个步骤。

1)包带接触力学分析采用非线性分析步。在每段包带的两端施加一对大小为50kN、方向相反的预紧力,模拟包带的张紧过程。为保证计算能够收敛,初始载荷步加载量为50N,在进行接触判断与平衡计算后,进行下一个载荷步的迭代,直至完成加载50kN的计算。

2)过载线性力学分析采用线性静态分析步。以某型运载火箭为背景,载荷条件为纵向10.5倍、横向1.8倍重力加速度。过载分析的基态继承了接触分析的结果并认为接触状态在过载分析过程中不发生变化。

分析的边界条件为适配器下端面固支约束。

3 仿真分析

3.1 对比分析

为评估包带约束对星箭连接环的影响,以某质量3 300kg、质心高度1.9m的卫星为研究对象,就是否考虑包带约束开展了两组分析。

首先采用工程上的简化分析方法,即不考虑包带约束,分析得到连接环的应力云图如图6所示。

图6 星箭连接环应力云图(无包带约束)

不考虑包带作用,星箭连接环的径向变形是均匀的,受过载变形后的星箭连接环仍近似为圆环状,最大Mises应力为204.3MPa。

若考虑包带约束与发射过载的组合作用,开展多步分析得到组合力学环境下的星箭连接环应力云图如图7所示。

图7 星箭连接环应力云图(考虑包带约束)

由图7可见,由于包带预紧力的作用,连接环端面不再是规则的圆形。星箭连接环上最大Mises应力为230.3MPa,位于连接环与承力筒连接的螺孔附近。

经比较可见,采用工程上的简化方法,得到的应力结果偏小了约30MPa。因此,当采用简化方法分析得到的应力接近材料屈服极限时,还应当考虑包带的约束作用,复核星箭连接环的强度。

3.2 承载能力分析

卫星质量、质心高度是影响过载力的关键因素,也是评价星箭连接环承载能力的主要标准。为评估星箭连接环对3 000kg卫星平台的适应性,针对此类卫星常见的一系列质量、质心高度组合,开展连接环组合力学分析,得出连接环上最大应力与变形如表2所示。

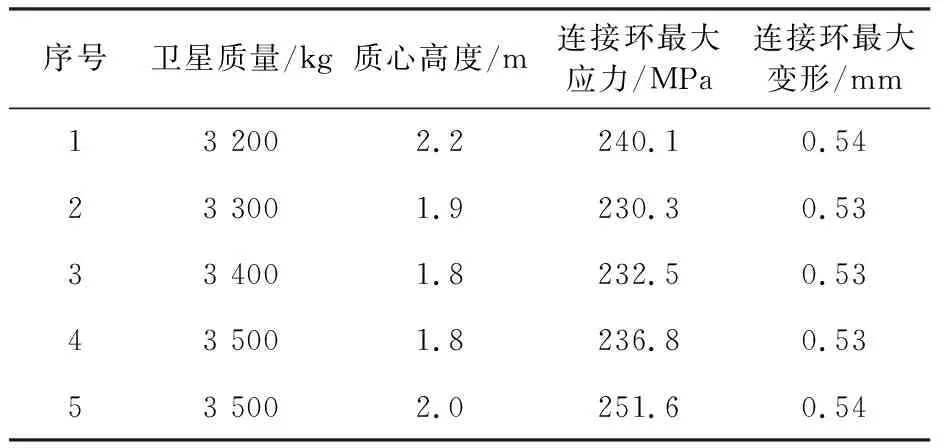
表2 不同承载下的连接环最大应力与变形

星箭连接环采用材料为铝合金,屈服极限为255MPa。依据表2,质量3 500kg、质心高度2m的卫星已经达到此型星箭连接环的承载上线。

4 结语

通过力学环境分解,综合利用ABAQUS软件的线性与非线性求解模块,分析得出了星箭连接环在组合力学作用下的应力与变形,并评估了其最大承载能力,具体如下:

1)包带约束作用使得星箭连接环的最大应力额外增加了约30MPa;

2)若采用工程上的简化方法,分析得出星箭连接环应力安全裕度低于0.15,则此时还应当考虑包带约束作用,应对星箭连接环的强度进行复核;

3)本型星箭连接环的承载极限为质量3 500kg、质心高度2m的卫星。