基于AMESim的多缸驱动液压机同步控制系统设计

郑黎明,鲁鹏涛

(1. 西安交通工程学院,陕西 西安 710300;2. 西安航天华威化工生物工程有限公司,陕西 西安 710100)

0 引言

液压机被广泛应用于工业生产等领域。针对当前多缸液压系统,谢金晶等[1]提出了内环压力控制和外环位置控制的方法;田英等[2]比较了串联型和并联型同步控制结构的同步误差,提出了并联型同步控制结构更适合液压缸同步控制的结论。这些方法虽然提高了多缸液压系统的控制精度和响应速度,但由于液压系统本身具有较强的非线性、时滞性以及惯性,造成液压机的各个液压缸很难保证位置同步[3]。因此,如何在保证液压机原有性能的同时,解决好各液压缸的位置同步问题,提高液压机的稳定性及可靠性,成为值得研究的问题。本文通过模糊控制理论对传统控制环节的优化,设计了一种具有PID控制环节的同步控制系统,提高液压多缸系统的同步精度与运行稳定性,扩大液压机的使用范围与效率。

1 液压机的结构参数与原理

1.1 基本结构参数

本文参照我校工程实训中心的YLS28-H型双缸液压机[4],其基本结构如图1所示,基本参数如表1所示。

表1 双缸液压机技术参数

图1 双缸液压机

1.2 液压机多缸驱动系统

1)基本结构

本文以1.1所示的YLS28-H型双缸液压机为基础,利用FluidSIM软件绘制了液压机多缸驱动系统原理图,如图2所示。

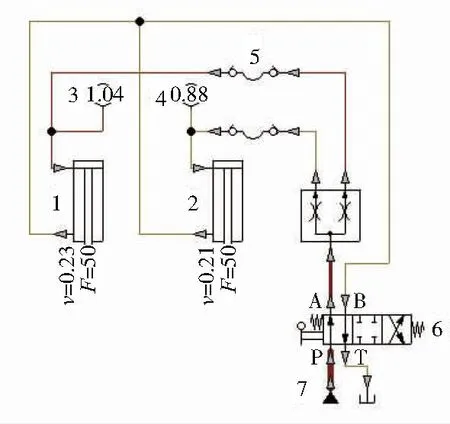
1—Ⅰ号工作液压缸;2—Ⅱ号工作液压缸;3、4—压力计;5—油管;6—控制阀;7液压源。图2 液压机多缸驱动系统原理图

2)仿真分析

如图2所示,在FluidSIM环境[5]中进行双缸液压机的系统仿真,其液压机系统中各工作液压缸的状态,如图3所示。

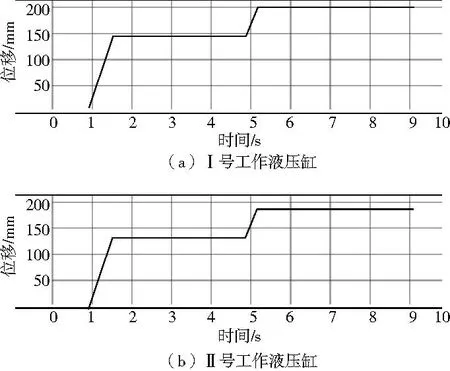
图3 工作液压缸的状态图

如图3所示,在FLuidSIM的仿真环境下,若液压源7的工作压力为16 MPa,液压泵流量为5 L/min,运行6 s时双缸液压机中的Ⅰ号工作液压缸输出压力P1=1.04 MPa,位移193.13mm;Ⅱ号工作液压缸输出压力P2=0.88 MPa,位移185.83mm。

通过FLuidSIM仿真发现,液压机在锻压过程中,面对于形状不规则的锻坯,坯料在各方向的流动具有不均匀性,即外部负载存在脉动变化情况。这时各个液压缸出现了位置不同步问题,造成了系统的不稳定性。

1.3 系统工作压力与分析

本文选取了图2中Ⅰ号、Ⅱ号工作液压缸为研究对象,在FLuidSIM仿真环境中得到了不同外部负载下Ⅰ号、Ⅱ号工作液压缸的工作压力及其相对位移变化量,如表2所示。

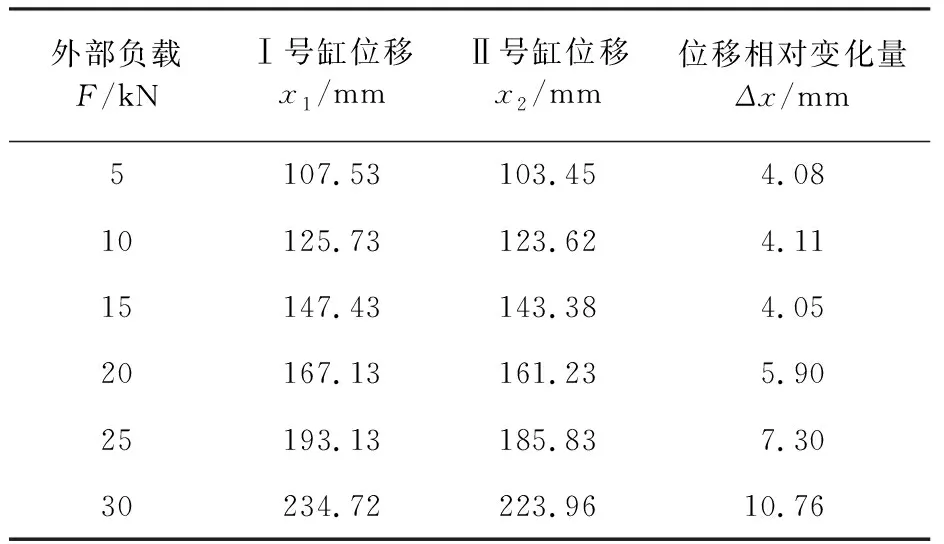
表2 外部负载与液压缸位移

本文在表2的基础上,构建了比例系数k的数学模型,利用MATLAB分析[6-7]并得到了比例系数。

(1)

可得k≈5.21。

2 同步控制系统与数学模型

本文以YLS28-H型双缸液压机的结构为基础,通过分析将其等效为2个阀控单作用液压缸,并引入PID控制环节[8-9],其控制系统原理图如图4所示。

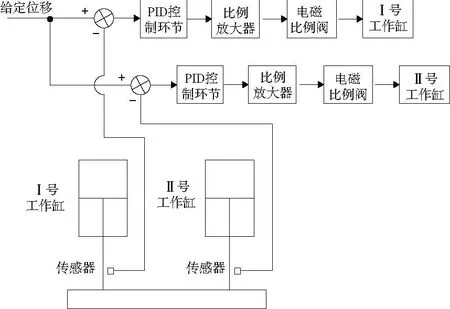
图4 同步控制系统原理图

由于弹性负载很小可以忽略不计,液压缸被视为1阶积分环节与2阶环节的组合,其传递函数为

(2)

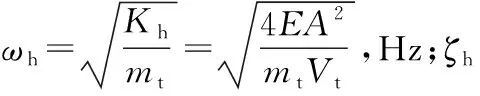
比例阀一般被视为2阶振荡环节,其传递函数为

(3)

式中:s为比例阀活塞面积;kq为比例阀流量增益;ωv为比例阀的固有频率;ζv为比例阀的阻尼比。

系统的传递函数为

(4)

(5)

依据式(1)及元件选型,位移传感器的增益kf=1.25;PID控制环节的比例系数kP=5.21;系统的开环放大增益kq=0.15×10-3;系统固有频率ωh=150.2 Hz;系统阻尼比ζh=0.2;比例阀的固有频率ωv=350 Hz;比例阀的阻尼比ζv=0.7。

综上所述,得到系统的开环传递函数

(6)

根据闭环控制系统原理框图和各环节传递函数,在MATLAB Simulink[10]窗口中选取对应模块建立双缸液压机PID控制系统的仿真模型,并进行线性分析,得到液压系统阶跃响应曲线,如图5所示。

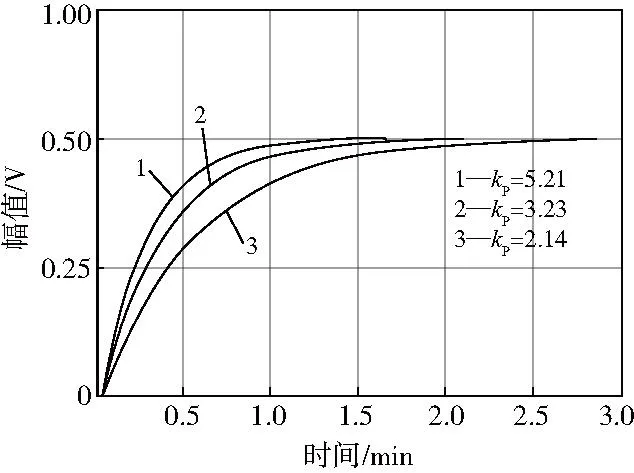
图5 液压系统阶跃响应曲线

比例系数kP分别取2.14、3.23、5.21时,系统的阶跃响应由图5可知:随着kP的增大,系统的动态响应明显改善,响应时间进一步缩短。通过调试及经验,文中PID控制器的参数为P=5.21、I=4.8和D=0.01。

3 同步控制系统的仿真与分析

3.1 建立仿真模型

从AMESim软件[11]的“Signal,Control”电子器件库;“Hydraulic”液压库;选取相应的“元件”进行相应系统草图的绘制,如图6所示。

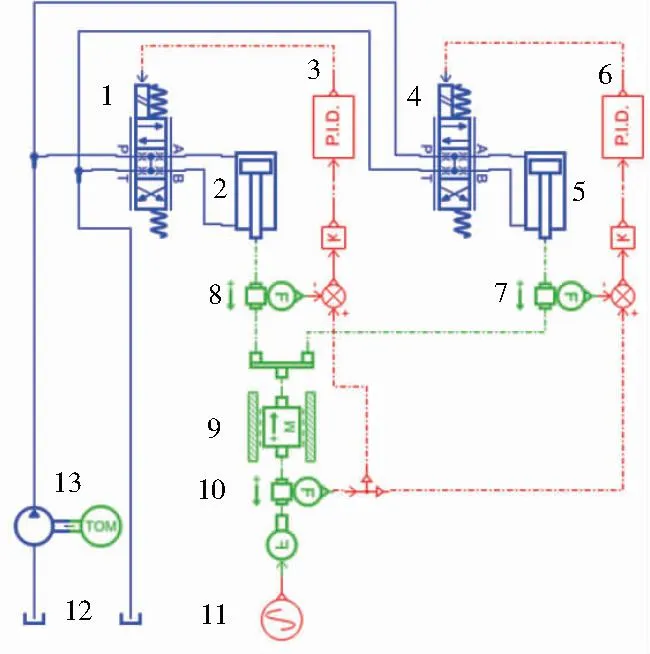
1、4—电磁比例换向阀;2—Ⅰ号工作缸;3、6—PID环节;5—Ⅱ号工作缸;7、8、10—传感器;9—负载质量块;11—控制信号;12—油箱;13—液压泵。图6 同步控制系统的仿真模型

3.2 设定子模型参数

依据图2、图4、图6,本文给出了液压机同步控制系统的基本参数,为后续液压机同步控制液压系统的仿真提供了依据,如表3所示。

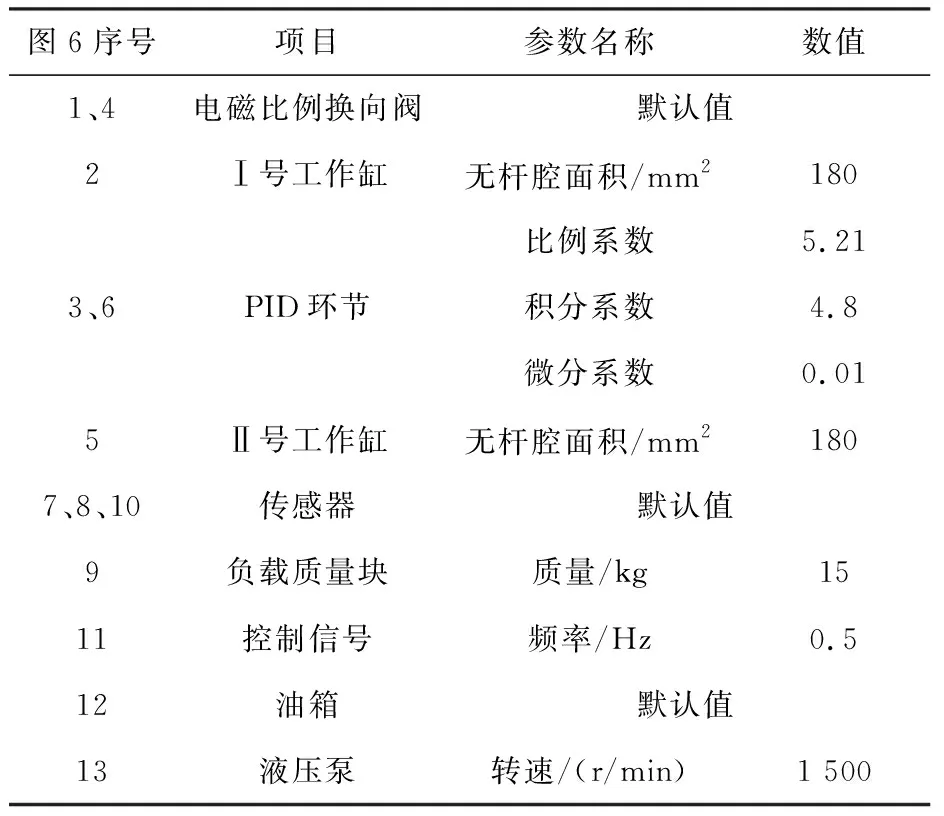
表3 PID同步控制系统仿真模型参数

如图6所示,处于工作状态时,液压机液压系统中的Ⅰ号工作液压缸2、Ⅱ号工作液压缸5以一定速度伸出,驱动液压机下降进行锻压等工作,同时质量块前端的压力传感器10与Ⅰ号液压缸压力传感器7、Ⅱ号液压缸压力传感器8分别组成控制系统反馈回路,得到压力变化的增量后,PID控制环节工作,并按照预定算法向电磁比例阀1、比例阀4输入相应比例控制电流,使液压系统成比例输入压力,提高液压机稳定性。

3.3 系统的仿真与分析

1)系统仿真

本文依据3.1中的仿真模型,按照表3中的参数进行设置并进行仿真,得到一般控制系统的位置变化曲线,如图7所示;PID同步控制系统的位置变化曲线如图8所示。

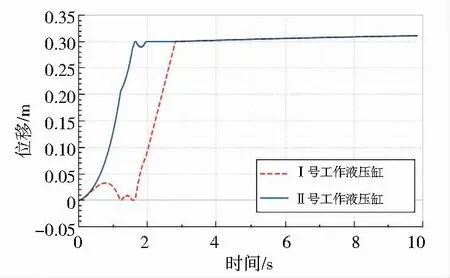
图7 一般控制系统位置变化曲线

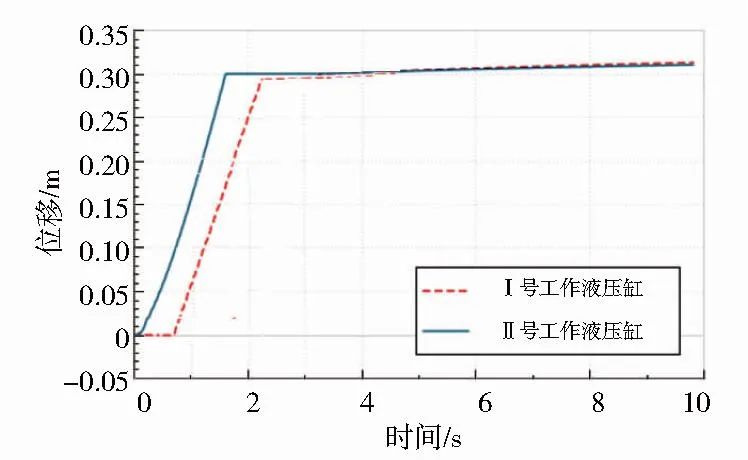
图8 PID同步控制系统位置变化曲线

由图7可知,在采用一般控制系统时,Ⅰ号、Ⅱ号液压缸工作时存在一定的位移波动,且两缸的位移偏差较大。由图8可知,当采用PID控制系统时,Ⅰ号、Ⅱ号液压缸工作时位移波动明显减小,且两缸的位移偏差进一步减小。

2)结果分析

结合图8,通过多次仿真实验得到采用PID同步控制系统后Ⅰ号、Ⅱ号液压缸工作的位移数据,如表4所示。

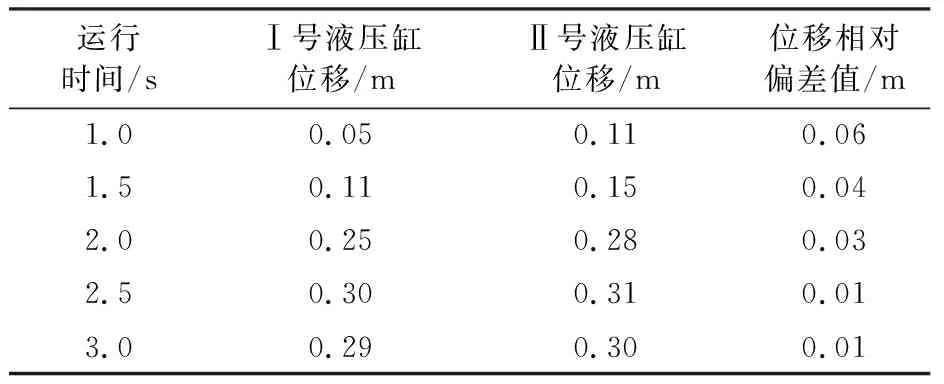
表4 仿真实验数据

如表4所示,通过对PID同步控制系统的仿真结果进行数据的分析,在2 s后Ⅰ号、Ⅱ号液压缸的位移偏差明显减小,实现了同步控制。

3)系统频域仿真

依据图7与图8中的仿真运行结果,分别对二种控制系统的运行结果进行频域分析,并对结果进行比较分别如图9和图10所示。

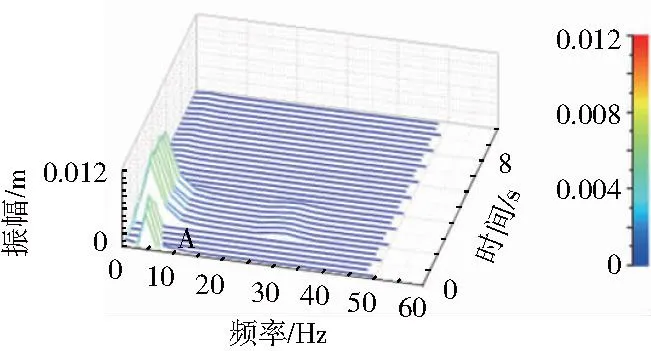
图9 一般控制的位置频域曲线

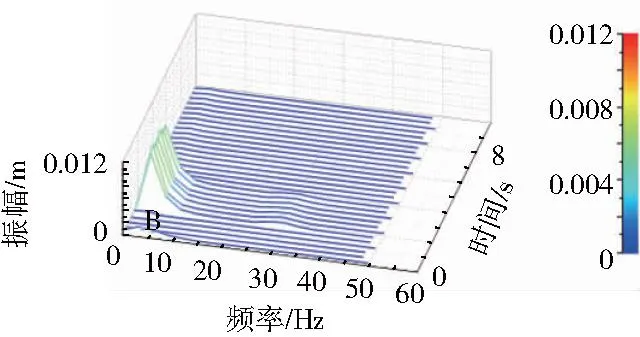
图10 PID控制的位置频域曲线

通过频域分析发现,图9中A处Ⅰ号、Ⅱ号液压缸在液压机工作的开始阶段,存在一定的位移波动,而这时,在相同时间与外部振动载荷的作用下,将图10中B处的状态与图9中A处相比较,位移波动与偏差明显进一步减弱。通过分析证明PID控制系统起到了较好的补偿效果,提高了双缸液压机的稳定性,达到了同步控制的设计目标。

4 结语

本文首先分析了液压机液压系统的结构与工作原理,通过分析与仿真发现传统的控制方式造成了一定的工作液压缸的位置偏差。其次,针对位置偏差造成的不同步问题,文中设计了一种具有反馈环节的PID控制系统,通过PID控制向工作系统成比例进行压力输入,进而起到补偿作用。最后,以AMESim为手段搭建了PID同步控制系统的仿真模型,并进行了仿真分析。通过仿真结果的对比分析,表明PID同步控制系统对液压系统所造成的压力损失进行了有效补偿,保持了多缸液压机各液压缸所需压力,提高了多缸液压机运行的同步性,具有一定的应用价值。