面向卫星电源系统的一种新颖异常检测方法
张怀峰,江 婧,张香燕,皮德常
(1. 南京航空航天大学计算机科学与技术学院,南京 211106;2. 北京空间飞行器总体设计部,北京 100094)
0 引 言
卫星电源系统的主要功能包括产生、储存、变换、调节和分配电能,是卫星系统的重要组成部分。由于外太空环境复杂,卫星电源系统在轨运行期间不可避免地会出现一些异常,影响卫星的正常运行,及时有效地检测卫星电源系统的异常,对保障卫星正常运行具有重要意义。
近年来,相关学者提出了一些基于传统机器学习方法的卫星电源系统异常检测算法。Pan等[1]利用关联规则挖掘的方法发现电源系统各个零部件之间的关联规则,然后使用核PCA(Principal components analysis)进行异常检测,该方法充分利用了卫星分系统各个零部件产生的数据;康旭等[2]针对遥测数据维度过高,首先计算某一属性和该属性方向平行线的余弦值,通过度量余弦值,筛选出异常相关属性,然后使用筛选出的属性进行异常检测;李楠等[3]针对自旋稳定卫星提出了一种数据驱动的异常检测方法,该方法使用卫星姿态与传感器之间的冗余关系作为判断异常的依据,并用主成分分析量化这种冗余关系,通过比较主成分子空间的特征值和残差子空间的特征值来判定异常,通过仿真试验验证了方法的有效性;金洋等[4]针对传统的定性模型诊断方法推理规模过大,不能达到航天器异常检测的实时性要求的困难,提出了解析冗余计算方法和扩展候选产生算法,通过控制规模降低计算量,提高异常检测效率。
由于卫星电源系统具有众多零部件,每个零部件都包含一个或多个参数,并且卫星运行过程中会周期性地经过地球的向阳面和背阴面,电源系统会做出相应的充放电动作。因此其产生的数据具有维度高、周期性明显的特点。针对该系统某一个或多个特定参数进行异常检测,往往不能反映出系统的真实状态,而使用所有参数进行异常检测,传统的机器学习算法又面临着“维度诅咒”的困难,用于异常检测时往往检测速度慢且效果不佳。
近年来深度学习在计算机视觉、语音识别和自然语言处理等领域都取得了优秀的成果。在异常检测领域,采用基于深度学习的堆叠自编码器(Stacked auto encoders,SAE)实现异常检测愈来愈受同行学者的关注。Sun等[5]提出了一种基于深度神经网络的发动机异常检测方法,其首先使用稀疏自编码器进行特征提取,然后使用提取到的特征训练神经网络进行异常检测,该方法取得了较好的检测效果;Wang等[6]为了检测变压器异常,提出了一种自编码器-连续稀疏自编码器(Continuous sparse auto encoder,CSAE)用来学习特征,CSAE在激活函数部分加入高斯随机单元来学习非线性数据的特征,然后使用学习到的特征进行异常检测。当前已有的基于自编码器的异常检测方法通常在使用自编码器进行降噪滤波和特征提取,对提取到的特征使用其他分类算法进行分类,这种方式通过少量数据训练就可以得到较好的异常检测效果,充分发挥了堆叠自编码器强大的特征提取能力。
卫星电源系统产生的数据具有维度高的特点,直接将SAE用于卫星电源异常检测面临着如下困难:
1)若直接使用电源系统产生的高维数据训练SAE,即将每个时刻产生的数据作为训练样本输入SAE,这样虽然充分利用了电源系统各个参数的数据,但是将每个样本当做了孤立的样本,丢失了时间维度上的信息,割裂了数据的相关性。
2)若针对某一个具体参数,采用固定长度的数据作为训练数据输入到SAE,则没有充分利用电源系统的其他参数,并不能反映出电源系统的真实状态,且无法准确地检测出异常发生的时刻。
针对上述困难,本文通过改进SAE的损失函数和训练算法,提出了一种新的代表性特征自编码器(Representative feature auto-encoder,RFAE),用来对卫星电源系统进行无监督的异常检测。本文主要贡献如下:
1)SAE的损失函数一般只衡量重构样本和原始样本之间的误差,本文提出了一种既能衡量SAE重构样本和原始样本之间的误差,又能衡量SAE重构样本之间误差的损失函数,称之为差异函数(Difference function, DF)。
2)提出了一种面向周期性时序数据的训练算法(Periodic data training algorithm, PDTA)。该算法根据相位对时序数据进行分组,相位相同的样本划分为同一组,保留了时序数据的周期信息,并通过核密度估计解决每个分组内数据量少的问题。
3)结合本文提出的损失函数DF和训练算法PDTA,然后又提出了代表性特征自编码器(Representative feature auto encoder, RFAE)并用于卫星电源系统异常检测。相比SAE,RFAE能够提取到相位相同样本的代表性特征,根据代表性特征重构样本,通过衡量重构样本和原始样本之间的误差检测异常。相比于目前的异常检测算法,RFAE不限制输入数据的维度,充分利用了电源系统各个参数的数据,并且PDTA训练算法保留了时序数据的周期性信息。通过模拟数据和真实数据分别进行了对比试验,RFAE均优于目前最新的相关算法。
1 方法概述

图1 RFAE异常检测流程Fig.1 RFAE anomaly detection process
RFAE异常检测的整体流程如图1所示。其中损失函数使用了前文提出的差异函数DF,差异函数综合了原始样本和重构样本之间的误差以及重构样本之间的误差,使RFAE学习能到代表正常样本的特征,称之为代表性特征。
图1中的虚线部分为训练过程。RFAE的训练算法使用了前文提出的周期性数据训练算法PDTA。PDTA首先将周期性时序数据按相位进行分组,相位相同的样本划分为同一组,如图1中原始数据长度为n,周期为p,按相位进行划分后得到p组数据,每组约有n/p条数据。为了用更多的数据训练RFAE,PDTA使用核密度估计算法估计每组内的样本分布,根据估计的样本分布生成新的样本,从而达到增加每组样本数量的目的。在训练阶段,PDTA每次从同一组内选择数量为b的样本,然后使用反向传播和Adam算法[7]使DF最小化,从而可以学习相位相同样本的代表性特征。
图1中的实线部分展示了异常检测过程。RFAE根据代表性特征重构样本,计算重构样本和原始样本之间的误差,若误差大于阈值则判定样本为异常,从而达到异常检测的目的。
2 堆叠自编码器和核密度估计
RFAE是基于堆叠自编码器的异常检测模型,且PDTA算法需要核密度估计来生成新的数据,下面简要介绍堆叠自编码器和核密度估计。
2.1 堆叠自编码器
自编码器是一种神经网络,经过训练后能尝试将输入复制到输出。自编码器内部有一个隐藏层,可以产生编码h来表示输入。该网络由两部分组成:一个由函数h=f(x)表示的编码器和一个生成重构样本的解码器r=g(h)[8]。堆叠自编码器由若干自编码器堆叠而成,包含有多个隐藏层。
堆叠自编码器在学习过程通过调整网络参数W和b,最小化损失函数L(x,r)。损失函数L惩罚r与x的差异,如均方误差:
(1)
通常为了使自编码器学习到的特征更加鲁棒,可对损失函数加入权值衰减约束和稀疏性约束。
2.2 核密度估计
密度估计是一种根据观察到的样本,对整个数据集分布做出估计,进而得到整个数据集的概率密度函数的方法[9]。Rosenblatt[10]和Parzen[11]提出了一种非参数估计方法,称为核密度估计。由于核密度估计不利用有关数据分布的先验知识,对数据分布不附加任何假定,是一种从样本本身出发研究数据分布特征的方法,在统计学领域均得到了广泛使用。
核密度估计将直方图估计的思想做了推广。如果根据样本X1,X2,…,Xn,做出带宽为h的直方图,则对于点x处的密度估计可以写成
(2)
其中,k是区间(x-h,x+h)内的样本数目,这个估计可以写成
(3)
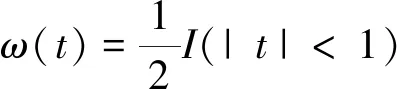
核密度估计将权重函数ω(t)替换为其他函数K(·),K(·)称为核函数,且

(4)
假设K(·)是一个原点为中心的对称概率密度分布,那么有
(5)
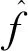
h=0.9min(S,Q/1.34)n-0.2
(6)
3 代表性特征自编码器
本节介绍RFAE的异常检测过程,分3小节分别介绍差异函数DF、训练算法PDTA和RFAE的异常检测算法。
3.1 差异函数
为了方便表述,首先引入物理学中相位的概念。相位是对于一个波,某一时刻这个波在循环中的位置。在周期性时序数据中,不同周期的数据相对于这个周期起点的位置,称为相位。易知,在周期性时序数据中,如果两条数据的相位相同,那么这两条数据的值也相同。
卫星电源系统产生的是周期性高维时序数据X=x0x1,…,xn-1,记时间序列X的周期为p,xi是在时间为i时产生的数据,含有d个参数,总时长为n,不妨设X共有k个周期,即n=kp。将卫星电源系统正常状态产生的数据称为正常样本数据,简称正常样本。异常状态产生的数据称为异常样本数据,简称异常样本,检测卫星电源系统异常也即是检测出X中的异常样本。
由于X具有周期性,若xi和xi+cp,c=0,1,…,k-1都是正常样本,则xi和xi+cp相等。即相位相同的正常样本,样本的值也相等。由于实际上样本会受到噪声的影响,因此有
(7)
将xi和xi+cp划分为同一组,则X可划分为p组,如式(8)。
(8)
其中,Si组内的数据具有相同的相位,称Si为一个分组。如果分组Si内的样本都是正常样本,则Si内的样本应该是近似相等的;若Si内有异常样本,则由于异常样本相比于正常样本数量较少,因此Si内的大多数样本也都是正常样本,而只有少量异常样本。研究要求自编码器学习到Si中可以表示大多数正常样本的特征h,而忽略其中的数量较少的异常样本,称h为代表性特征。将重构样本与原始样本之间的误差称为重构误差,根据同一个分组Si内的样本生成的重构样本之间的误差称为组内误差。根据h重构的正常样本r具有如下特点:(1) 重构样本与原始样本差异较小,即重构误差较小;(2) 同一分组重构样本之间的差异较小,即组内误差较小。重构误差可以用式(1)来衡量。对于组内误差,首先计算重构样本两两之间的距离
D={d00,d01,…,di(k-1),d(i+1)0,…,d(k-2)(k-1)}
(9)
其中,dij是重构样本ri和rj之间的距离。为了衡量重构样本之间的差异,有
R=μ(D)+σ(D)
(10)
其中,
(11)
(12)
式(11)计算D的均值,式(12)计算D的标准差。从而可知,R越小则重构样本之间的差异越小,即组内误差越小,反之则反。
经过上述分析,得到用来提取代表性特征的损失函数
L(x,r)=μE+νR
(13)
其中,E用以衡量重构误差,R用以衡量组内误差,称上式为差异函数DF,其中系数μ,ν取值范围为[0,1],当μ/ν→0时,重构误差可忽略不计,堆叠自编码器仅最小化组内误差;当μ/ν→∞时,组内误差可忽略不计,堆叠自编码器仅最小化重构误差。
3.2 周期性数据训练算法
如3.1节所述,在使用DF作为损失函数时,为了使堆叠自编码器可以学习相同相位样本的代表性特征,需要对训练数据按相位进行分组,相位相同的样本划分为同一组。为了提高每个分组内数据的数量,对每个分组内的数据进行核密度估计。然后从估计的概率分布中采样出一部分样本,并把它们加入到相应的分组,作为对原始数据的补充。然后从每个分组内选出若干样本进行训练,使用梯度下降和Adam算法最小化损失函数,即DF函数。称该算法为周期性数据训练算法PDTA。
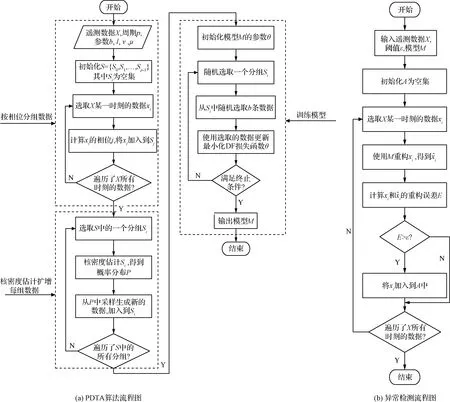
图2 算法流程图Fig.2 Flow chart of the algorithms
PDTA算法流程如图2(a)所示。PDTA首先对原始的高维时序数据X按相位进行分组,然后对每个分组内的数据进行核密度估计,得到相应的概率分布P,从P中采样出一定数量的样本,加入到对应的分组中。在训练阶段,算法随机选取一个分组,然后从这个分组中选出b条训练数据,使用反向传播和Adam算法训练RFAE。
以DF为损失函数,并且使用PDTA算法进行训练的堆叠自编码器可以提取到高维周期性数据的代表性特征,研究把这种堆叠自编码器称之为代表性特征自编码器RFAE。
3.3 异常检测
RFAE提取到的是代表性特征,该特征表示的是每个分组内的正常样本。根据该特征重构样本时,若原始样本是正常样本,则重构样本和原始样本差异较小,即重构误差较小;若原始样本是异常样本,由于代表性特征并不能准确的表示异常样本,因此重构样本和原始样本差异较大,即重构误差较大。基于这一点,通过重构误差来检测异常。检测算法流程如图2(b)所示。对于每个样本xi,通过训练好的RFAE模型M生成其重构样本,然后根据式(1)计算重构误差,若重构误差大于某一个阈值ε,则该样本被判定为异常样本,否则为正常样本。
4 模拟数据实验
首先通过模拟数据检验RFAE模型的有效性。模拟数据集含有100个参数,共有100000条数据。为了生成和卫星电源系统遥测数据相似的高维周期性数据,从正弦函数y=0.5(sin(a(x+b))+1)中产生每一个参数的100000条数据。其中a=π/50,b=0,1,2,…,99,每个参数都对应着一个b的值。由此可知,模拟数据的周期为100。对于生成的模拟数据,添加均值为0,方差为0.01的高斯噪声。从模拟数据中随机选取1000条数据,其中每条数据随机选取4个参数,将这4个参数对应的值增加或减少10%,将这1000条数据作为异常数据。最后,将所有数据进行归一化处理。
为了检验DF损失函数和PDTA算法的有效性,首先在模拟数据上进行对比试验。试验参数设置如表1所示。三个模型的结构相同,包含7个隐藏层,每个隐藏层神经元的数目为[50,20,10,5,10,20,50]。SAE1和SAE2采用了相同的损失函数,都是均方误差函数;但是训练算法不同,其中SAE1采用了神经网络常用的训练算法,即从训练数据中随机选取批量数据进行训练;SAE2采用了本文提出的PDTA算法。SAE2和RFAE均采用PDTA作为训练算法,但SAE2采用均方误差作为损失函数,RFAE采用DF作为损失函数。其中训练轮数设为15,学习率l=0.005,批量大小b=15,u=1,ν=0.00001。在异常检测阶段,将样本按重构误差从大到小排序,前1000个样本被预测为异常样本。三个模型准确率随训练轮数的变化如图3所示。

表1 模拟数据实验模型设置Table 1 Model setting of synthetic data experiment
图3中SAE1的准确率变化始终在0~0.2范围内波动,并不能准确地检测出异常数据;SAE2相较于SAE1,准确率有所提升,但并不稳定;RFAE检测效果最佳,最终准确率达到了1并且稳定在这一水平。由SAE1和SAE2的准确率曲线对比可知,PDTA算法对于异常检测效果有一定的提升;由SAE2和RFAE的准确率变化曲线可知,DF损失函数相较于MSE损失函数,对异常检测效果也有提升。即RFAE对于异常样本的重构误差大于SAE对于异常样本的重构误差。根据重构误差,将正常样本和异常样本分开,进而达到异常检测的效果。详细分析将在下一节真实数据实验中介绍。
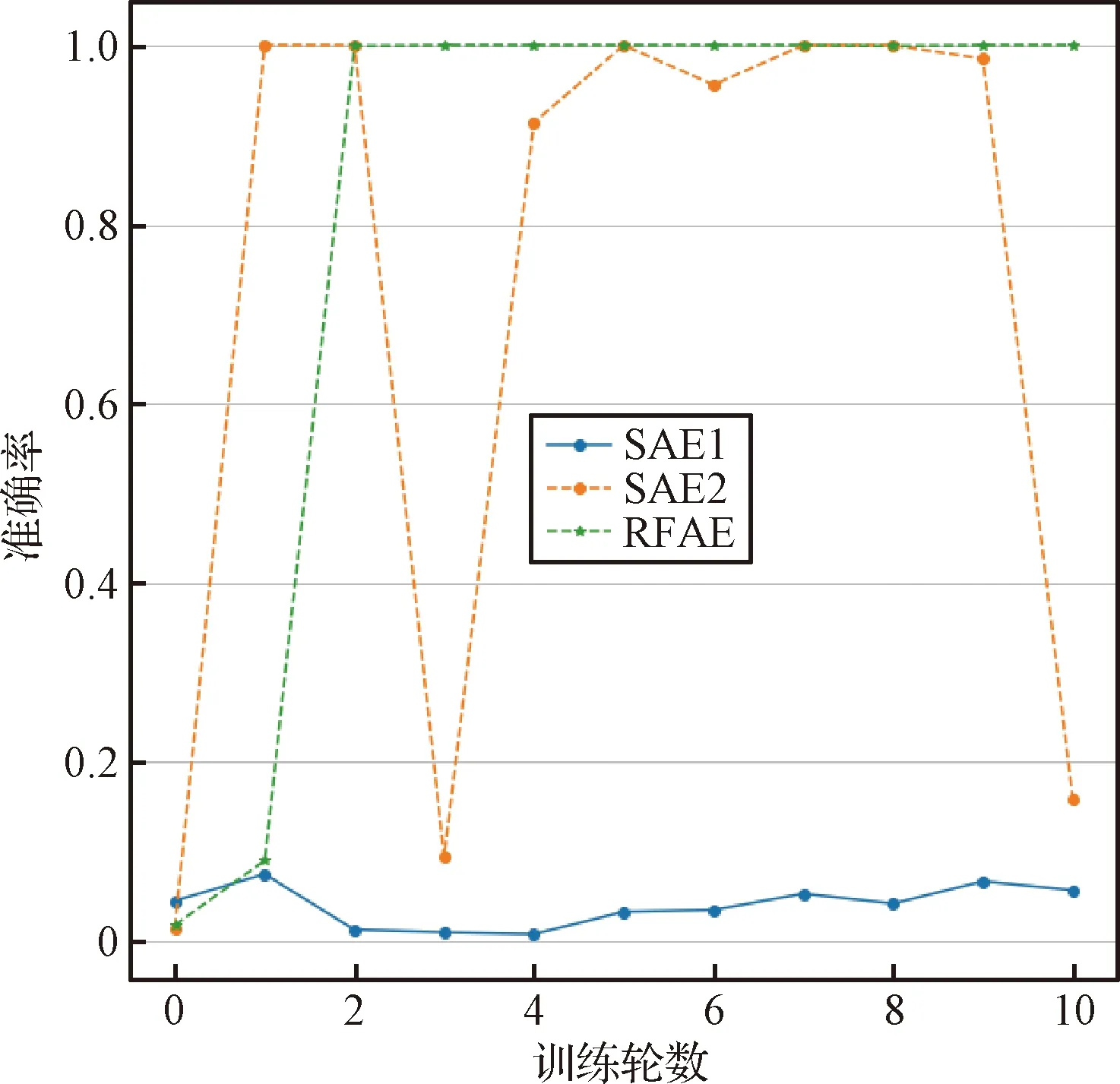
图3 准确率变化曲线Fig.3 Accuracy curve
5 卫星电源系统遥测数据试验
本试验采用的数据是2014年1月1日至2014年12月31日某在轨卫星电源系统76个参数的数据。电源系统每隔一定时间段下传一次各个参数的数据,12个月大约有2.33×107条数据。本试验使用RFAE分析这些数据,并检测卫星电源系统发生的异常。
5.1 数据预处理
卫星遥测数据不可避免地会受到天地传输网络的影响,从而产生野值。如果保留野值,算法会认为是异常导致误报,因此需要剔除野值。实际中卫星异常通常会持续一段时间,而野值通常只出现在某一时刻,然后采用中值滤波过滤野值。
为了便于算法检验异常,需要将各参数的数据采样频率统一化,通过使用降采样,将各个参数采样频率降为1 min,数据压缩为525600条,其中异常数据约有1700条,使用这些数据来检测电源出现的异常。通过统计了异常数据的条数(如代号为2143的参数分别在2014年7月26日00:42-01:50、2014年8月17日22:07-22:53出现了异常,该异常共持续114 min,对应着114条遥测数据),得到的异常详细信息如表2所示。
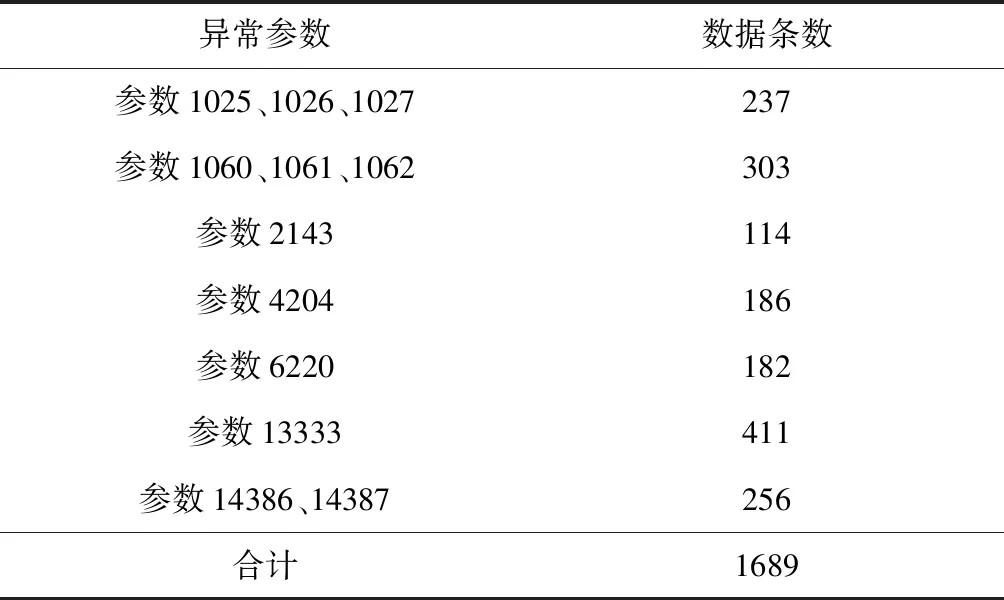
表2 异常信息Table 2 Anomaly information
5.2 电源系统异常检测
为了检验RFAE模型使用DF损失函数具有提取代表性特征的能力,将RFAE和SAE进行了对比试验。表3给出了SAE和RFAE模型的结构和损失函数。二者的网络结构相同,包含7个隐藏层,每个隐藏层神经元的数量为[40,20,10,5,10,20,40];SAE采用普通的神经网络训练算法,每个训练批次的数据从全体训练数据中随机选取,RFAE采用PDTA作为训练算法,每个训练批次的数据来自于同一个分组;SAE采样均方误差MSE作为损失函数,RFAE采用差异函数DF作为损失函数。

表3真实数据实验模型设置Table 3 Model setting of real data experiment
模型训练学习率设为0.005,训练轮数设为10,每个训练批次样本个数为15。在训练时,由于缺乏先验知识,无法准确地确定阈值。为了计算准确率,将训练中重构误差最大的前1700个样本预测为异常样本,然后计算训练过程中异常样本检测的准确率。训练过程中的准确率变化曲线如图4所示。训练完成后,最终RFAE检测异常准确率为97.9%,高于SAE的29.6%。这是由于SAE最终学习到的是所有样本的特征,无论是正常样本还是异常样本,SAE都可以比较准确地生成重构样本,导致异常样本和正常样本的重构误差相差不大,无法根据重构误差区分出正常样本和异常样本。相反,RFAE模型学习到的是代表性特征,仅能够比较准确地重构出正常样本,但是无法准确地重构出异常样本,即正常样本重构误差较小,异常样本重构误差较大,可以根据重构误差有效地区分出正常样本和异常样本。因此而导致RFAE模型准确率远远高于SAE。

图4 准确率变化曲线Fig.4 Accuracy curve
重构误差是检测异常样本的重要指标。图5和图6分别展示了SAE和RFAE正常样本和异常样本的重构误差分布直方图。由图5可知,SAE对正常样本和异常样本的重构误差分布情况基本一致,分布在[0,1]区间,并且随着重构误差的增大,样本频数减少,并不能通过重构误差明显地区分正常样本和异常样本。由图6可知,RFAE对正常样本和异常样本的重构误差分布情况明显不同,正常样本的重构误差分布在[0,2]区间内,而异常样本的重构误差大多集中在[3,8]区间内。根据重构误差的大小可以明显的区分出异常样本和正常样本,这再次证明了RFAE具有学习代表性特征的能力,从而提高了RFAE检测异常的能力。
为检验RFAE的有效性,根据训练后的模型,设置不同的ε值,根据ROC曲线(Receiver operating characteristic curve)确定最佳阈值约为ε=2.0053,此时假正率为0.38%,真正率为97.61%。确定阈值ε后,将RFAE和其他常用的无监督异常检测算法进行对比:
1) iForest,基于样本孤立性的异常检测方法[13]。
2) OCSVM,基于支持向量机的异常检测方法[14]。
3) PCA,基于主成分分析的异常检测方法[15]。
4) BoostSelect,基于集成技术的异常检测方法[16]。
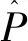
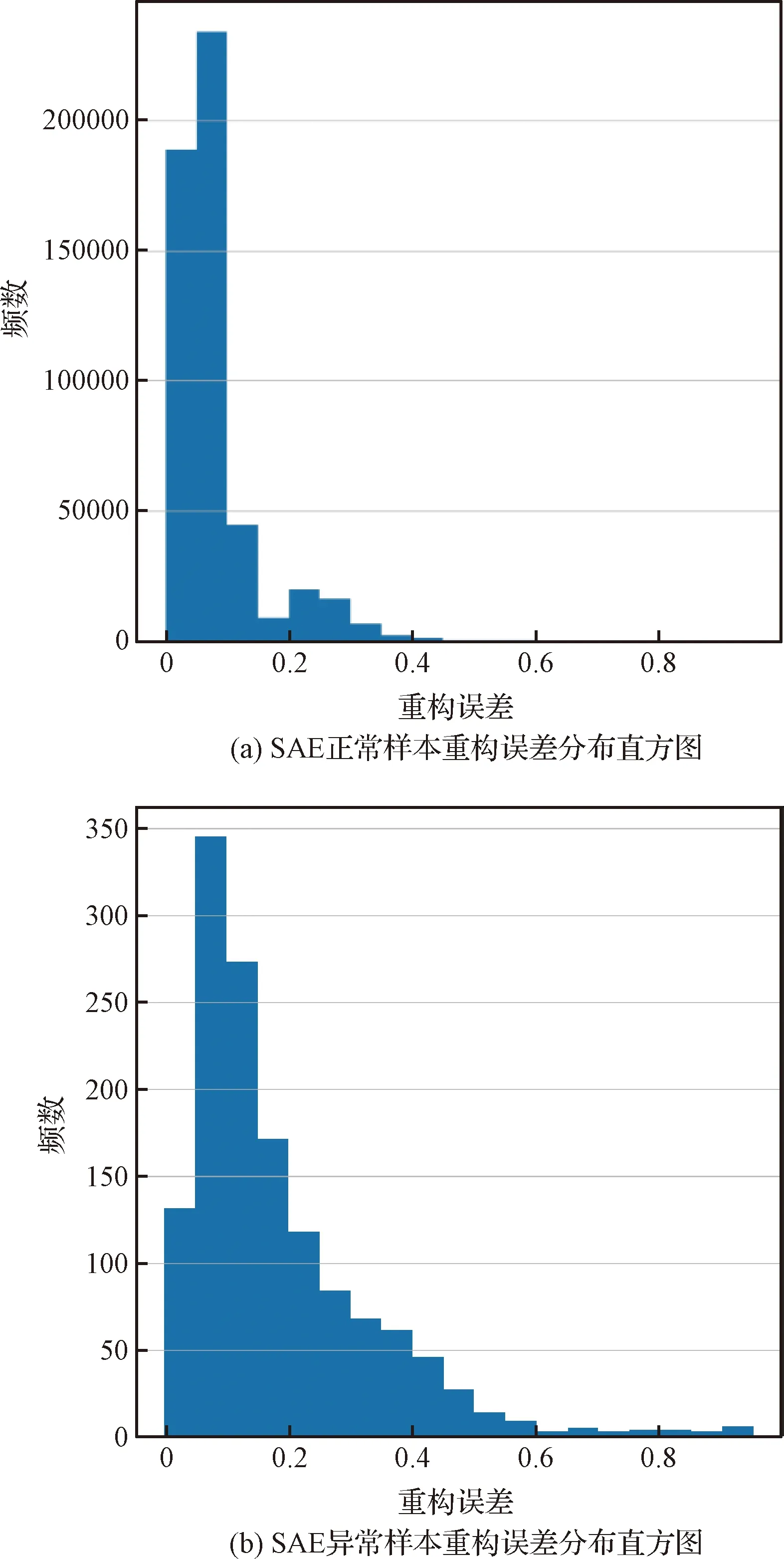
图5 SAE的正常样本和异常样本重构误差分布直方图Fig.5 Histogram of reconstructed error in SAE

图6 RFAE正常样本和异常样本重构误差分布直方图Fig.6 Histogram of reconstructed error in RFAE
由表5可知,其他算法由于数据维度较高,导致准确率低于RFAE。由于异常样本的数量远远低于正常样本,导致类别不平衡,从而预测为假正的样本数量较多。其他算法虽然召回率较高,但是精确率比较低。F值综合了召回率和精确率来衡量模型的优劣,由表5可知,RFAE算法的检测效果明显优于其他算法。此外,表5的最后一行展示了每个算法在预测阶段的运行时间,RFAE模型的运行时间最短,略低于PCA的运行时间,这是由于RFAE模型在训练完成后直接调用训练好的模型进行检测。综上所述,RFAE模型在预测效果和运行时间上均优于当前主流的异常检测算法。

(14)
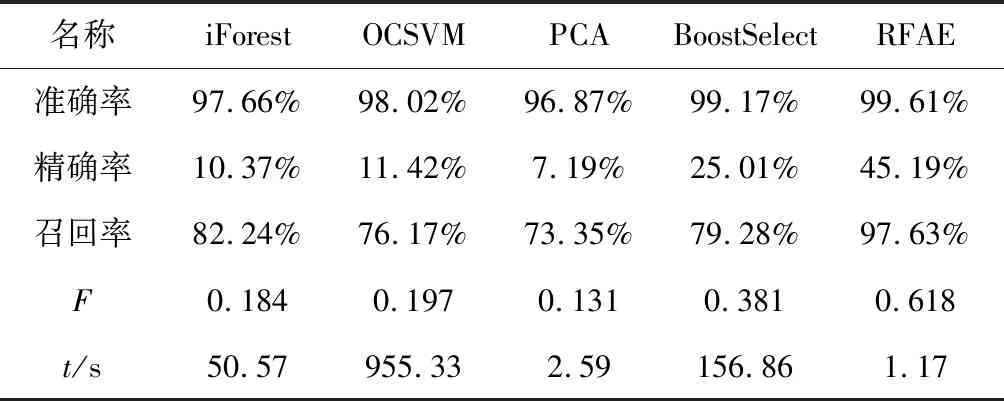
表5 异常检测结果对照表Table 5 Table of anomaly detection results
6 结 论
本文针对卫星电源遥测数据维度高、周期性明显的特点,提出了一种新颖的代表性特征自编码器RFAE模型,并用于异常检测。RFAE通过改进SAE的损失函数和训练算法,使得模型可以提取每个周期正常样本的代表性特征。通过代表性特征重构样本,根据重构误差来判断样本是否异常。相较于其他异常检测算法,一方面,RFAE不限制输入数据的维度,充分利用了电源系统遥测数据各个参数的信息,使得模型能够反映出电源系统的真实状态;另一方面,RFAE通过PDTA算法进行训练,保留了时序数据的周期性信息,从而能够反映电源系统随时间的变化情况。通过模拟数据和真实遥测数据分别进行了对比实验,RFAE均取得了优于当前主流异常检测算法的效果。此外,也为解决高维周期性时序数据的异常检测提供了一种新的解决思路。
未来将进一步研究下列问题:(1)RFAE异常检测阈值ε需要根据经验设置,在以后的工作中,将研究如何根据重构误差的分布情况由算法自动确定阈值,研究参数的自适应性;(2)电源系统会随着时间发生缓慢的性能退化,根据历史数据训练得到的模型是静态的,具有时效性,这和当前电源系统的状态有一定的偏差,这个偏差会随时间越来越大,从而导致模型检测效果变差。因此,在以后的工作中,团队将进一步研究如何降低卫星电源系统退化对异常检测效果造成的不良影响。
——编码器

