高考题之源:抛物线焦点弦为斜腰的特殊直角梯形
2020-01-10 06:39:08贵州省毕节梁才学校551700张玉彬
中学数学研究(江西) 2019年12期
贵州省毕节梁才学校 (551700) 张玉彬

图1图2
(1)AM1,A1F的交点P,BM1,B1F的交点Q在y轴上,且四边形PM1QF是矩形,M1F⊥AB,M1A,M1B是抛物线的切线,即焦点弦端点处的二切线垂直且交点在准线上.反之,过准线上一点M1作抛物线的二切线,切点分别为A,B,则AB过焦点F,且∠AM1B=90°,AB中点M与M1连线段MM1∥OF.


对抛物线C:x2=2py(p>0)(图2)也有对应结论.
纵观近10多年的高考题,发现抛物线的绝大多数题目都是利用上述结论按代数思路加工而成的,即对抛物线焦点弦与抛物线准线构成的特殊直角梯发掘而成,如2018年全国卷Ⅱ理19,2017年全国卷Ⅱ理16,2016年全国卷Ⅲ理20.2006年全国卷Ⅱ理21,2018年全国高考卷Ⅲ理16,2019年全国高考卷Ⅲ理21等.下面我们就利用上述结论,来解决2019年全国高考卷Ⅲ理21.

(1)证明:直线AB过定点;

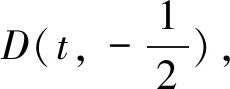
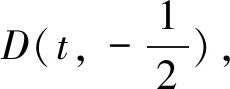

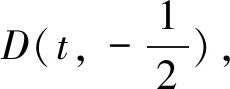
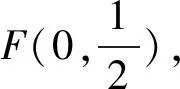


例2 (2018年全国高考卷Ⅲ理16)已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°,则k=.

解法2:F(1,0),|MF|2=5,由结论(2)得


总之,抛物线焦点弦构出的直角梯形图1,图2,内容丰富,命题者在该知识点上命题往往不拘泥于教材,因此,我们的教学应紧跟步伐,且应比命题者走得更远,方可应对高考.
猜你喜欢
中学生数理化·七年级数学人教版(2023年9期)2023-11-30 03:09:24
中学数学研究(江西)(2022年5期)2022-05-08 04:31:06
小学生学习指导(低年级)(2019年9期)2019-09-25 07:43:28
中学生数理化·七年级数学人教版(2019年4期)2019-05-20 10:03:44
高中生·天天向上(2017年7期)2017-09-25 02:42:08
中学生数理化·七年级数学人教版(2017年9期)2017-08-15 00:53:19
新高考·高一数学(2017年4期)2017-07-14 01:05:12
考试周刊(2016年66期)2016-09-22 13:54:18
淮北师范大学学报(自然科学版)(2014年4期)2014-07-04 06:21:46
福建中学数学(2013年1期)2013-03-06 01:46:00

