究竟错在哪里
——谈对一道中考题的异议
江苏省南京市金陵中学西善分校 (210041) 郭源源
近日,笔者在研究分式方程增根问题时发现,2011年黑龙江省齐齐哈尔市中考数学试卷中选择题第7题所给答案值得商榷,试分析如下:
一、原题呈现
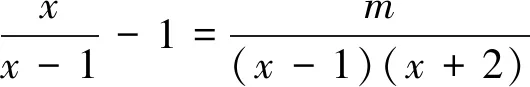
A.0和3B.1C.1和-2D.3
本题参考答案为D.事实上这个答案不正确,下面笔者从原题解答、错因追析、解析思考三个方面谈谈想法.
二、原题解答
查阅相关资料,参考答案选D的理由如下:
解:方程两边同乘(x-1)(x+2),得x(x+2)-(x-1)(x+2)=m,整理解得x=m-2.
因为原分式方程有增根,则x=1或x=-2.当x=1时,代入整式方程解得m=3;当x=-2时,代入整式方程解得m=0.
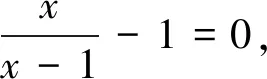
三、错因追析
1.多位思考,发现解法矛盾
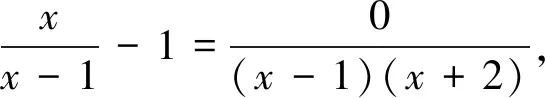
反过来想,分式方程去分母化整后,若整式方程有唯一解,则整式方程的这个解要不成为原分式方程的解,要不成为原分式方程的增根,只有这两种可能.而本题中若D正确,则原解中整式方程在m=0下的x=-2这个解,最后既不是原分式方程的解,也不是增根,那它是什么?此为矛盾之二.
2.借助矛盾,寻找错误根源
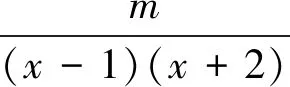
四、解析思考
数学家华罗庚说过:复杂的问题要善于退,足够的退,退到最原始而又不失重要性的地方,是学好数学的一个诀窍.笔者认为,要想彻底弄清分式方程增根问题,需退回到理解增根产生的原因.即去分母的依据是等式的基本性质,可等式的基本性质中同乘或除以的必须是一个不为0的整式,而分式方程去分母却无法保证同乘的最简公分母是否为0,故这一步是有漏洞的,因此最后的解需要代入最简公分母中检验,若不为0,则去分母步骤成立,解也没问题;若为0,则去分母步骤错误,最后的解也就成为了增根.归根到底,增根产生的原因是去分母同乘了0,导致未知数的取值范围被扩大.所以原题中的分式方程,去分母化整后,依据增根推出的m=0或m=3,步骤是严谨的,思维是全面的,两个值都符合题意,无需代入检验.
由此可见,分式方程的增根和失根问题往往是变形过程违反了方程的同解原理,是思维不严谨的体现.[2]只有站在概念本质和解法原理的角度审视出现的问题,追析错因,才能真正帮助学生从数学内涵和数学发展上更清晰更深刻地认识数学知识.

