水速对潜射导弹出筒流场和弹道影响*

李仁凤，胡晓磊，王正鹤，乐贵高

（1.郑州航空工业管理学院航空工程学院，郑州 450046；2.安徽工业大学机械工程学院，安徽 马鞍山 243002；3.南京理工大学机械工程学院，南京 210094）

0 引言

潜射导弹出筒阶段物理现象复杂，导弹的瞬态运动、筒口气泡的变化和海水扰动共同构成了复杂的力学环境。出筒过程中的燃气、水、水蒸气介质相互作用，产生质量、动量和能量不断交换，对水下发射流场和发射装置载荷有很大影响。针对潜射导弹出筒过程流动状态，综合经济性和计算精度两方面，数值模拟是目前主要采用的研究手段。国外学者Dyment［1］等基于VOF 模型模拟和实验验证了航行体出筒过程尾部空泡的形成。Weiland［2］等开展了不同水深和横流条件导弹出筒过程流场计算。国内刘筠乔［3］等数值模拟了导弹水下垂直发射出筒过程通气空泡，获得了导弹的流体动力特性和通气空泡演化历程。王汉平［4］等基于VOF 模型和动网格技术研究了潜射导弹二维轴对称和三维模型下的筒口载荷、尾部气泡形态和筒盖受力。曹嘉怡、鲁传敬［5］等耦合分析了导弹出筒过程筒外气-水混合流场和导弹运动。王亚东、袁绪龙［6-7］等设计了锥形弹丸，并进行水下试验，数值计算了锥头锥角、发射深度和发射艇速对流场影响。刘传龙、张宇文［8］等首次考虑了适配器对潜射导弹出筒过程的影响。闵景新［9-10］采用数值方法对比研究了潜射导弹头部形状、重推比和发射深度参数对出筒阶段流体动力和肩空泡形态的影响。

水流速度对水下发射出筒流场的研究现有文献相对较少，文献中的研究多数未考虑入口动力源压强变化和肩部空化，本文以实际获得的弹射动力源压强作为输入，考虑了筒内均压气体的流出和导弹肩部空化现象，对比研究了不同水速下潜射导弹出筒过程流场、载荷变化规律。

1 物理模型

1.1 控制方程

基于Mixture［13］混合多相理论，忽略相与相之间滑移，即流场中的各相压强和速度相同，得到多相控制方程。

混合物连续性方程

混合物动量方程

能量方程

1.2 计算模型与边界条件

图1 为潜射导弹出筒阶段结构示意图，坐标原点位于初始时刻弹头中心处，x 方向为水流方向，z向为弹体轴向，y 向垂直于xoz 面。网格划分采用分块结构化网格划分策略，筒盖附近由于结构较为复杂采用非结构网格，其余位置均采用结构化网格，以保证计算精度；图2 为计算区域局部位置网格图。

水流入口采用速度入口边界条件，速度分别为v=0/1/2 m/s。动力源入口设为压力入口，入口总压变化规律如图3 所示，动力装置总工作时间为0.6 s，工作结束后入口边界改为wall；整个外流场边界设为压力出口，由于水压随着水深的改变而变化，因此，出口压强按照导弹实际所处的水深编写用户自定义程序udf 实现，文中初始时刻发射水深为30 m。

图1 潜射导弹出筒过程示意图

图2 出筒过程网格模型

图3 入口总压曲线

1.3 导弹运动方程

导弹水下发射出筒时，根据牛顿第二运动定律，导弹受到的合力可表示为：

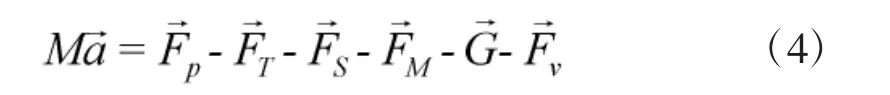
2 数值方法验证

潜射导弹出筒时产生的肩部空化和筒口气泡等一系列物理现象在理论分析、数值计算和实验测试方面均有一定难度，由于发射时间短，且发射环境复杂，导弹水下发射出筒的实验数据较难获取。本文采用间接验证方法，将文中建立的数值计算方法用于文献［14］半球头导弹水中运动模型，通过与试验数据的对比，验证文中数值方法的有效性。计算模型与文献［14］保持一致，图4 为导弹壁面压力系数计算值与实验值对比，横坐标为导弹距离弹头顶点的横向距离s 和导弹直径D 的比值，纵坐标压力系数Cp计算式为

式中，p 为弹体壁面某位置压强，pref为环境参考压强，vm为导弹运动速度，ρ 为水密度。

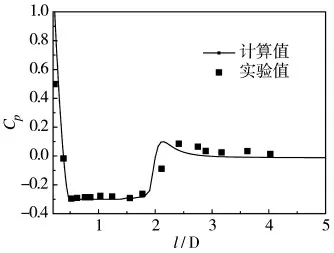
图4 导弹壁面压力系数计算值与实验值对比

由图可知，压力系数计算值与实验值［13］吻合较好，空泡起始位置为s/D=1.5 处，空泡闭合位置发生在s/D=2.0 左右，空泡长度基本一致，计算精度较高，采用的计算方法可用于本文潜射导弹弹射出筒段流场、载荷和弹道的计算。

3 计算结果与分析

3.1 流场分析

分别开展了v=0/1/2 m/s 3 种水流速度下导弹出筒过程流场计算。图5 为不同流速下筒口气泡形态。由图v=0 流速下气泡变化规律可知，在未出筒前，导弹与发射筒间的均压气体涌出，形成附着在弹体壁面的气泡，发射初期由于导弹速度小，气泡径向扩张速度要大于轴向拉长的速度，0.4 s 时导弹已经具备了一定的轴向速度，气泡在弹体的带动下被轴向拉长，径向扩张速度减小。弹体在0.6 s 时刻出筒，出筒后动力源提供的燃气蒸汽混合介质由筒口喷入水中，由于出筒时筒内的混合气体压强高于水压，因此，气体在水中膨胀形成较大筒口气泡，均压气体附着在弹体的气泡与筒口气泡融合。随着弹体运动，在其带动下，弹体尾部与筒口之间的气泡不断拉长，且在外界水压的综合作用下，0.9 s 时气泡在弹尾附近断裂。水速引起了筒口气泡的不对称，迎流面筒口气泡受到压力作用导致气泡向背流面偏移现象，最终导弹迎流面一侧附着气泡体积小于背流面一侧，引起弹体侧向偏转，随着流速增大，偏转越严重。

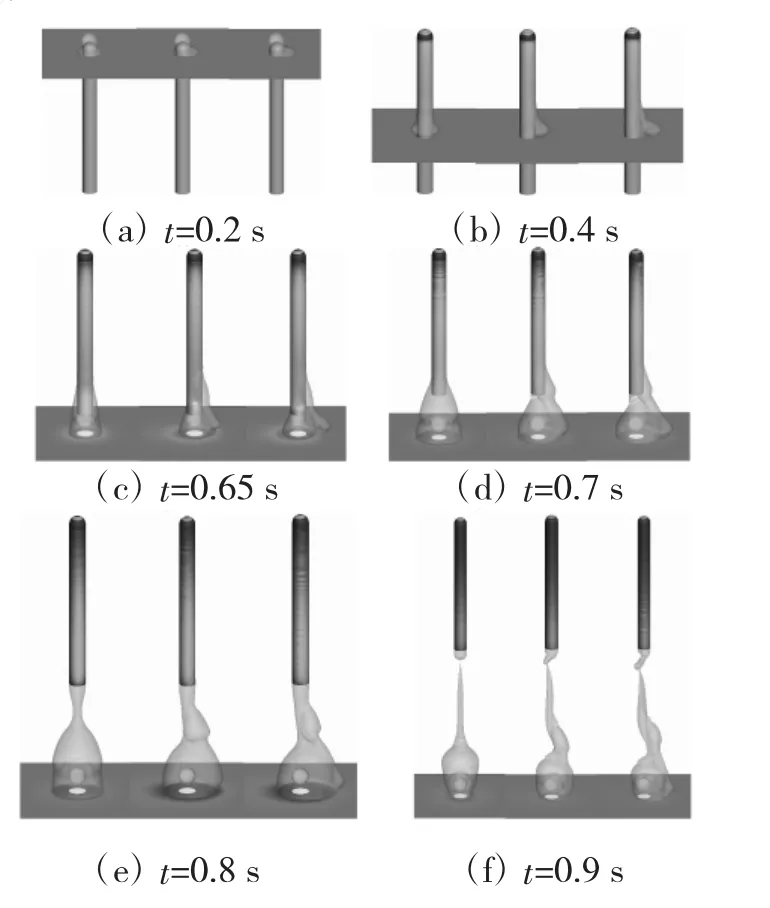
图5 不同流速流场气泡形态变化（v=0/1/2/m/s）

3.2 载荷分析

图6 为不同时刻导弹y=0 壁面上的压强变化。导弹出筒前t=0.2 s 和t=0.4 s 时刻，由于弹体速度小，其绕流作用相对较小，由图可知，距离导弹头部相同位置壁面处迎流面上的压强值要高于背流面，且其低压位置的起始高度距离弹头较远，结束位置距离弹头较近，因此，在导弹头部绕流作用下引起的迎流面肩部低压范围总长度要小于背流面。随着流速的增加，其迎流面上的压强更大，背流面压强更小，这将产生更大的侧向力。由于适配器的限制，弹体在出筒前尾部受流速影响较小。导弹出筒后，t=0.7 s 时刻v=0/1/2 m/s 流速下弹体迎流壁面上的空泡长度分别为0.254 l0/0.222 l0/0.141 l0，背流面上的空泡长度分别为0.254 l0/0.304 l0/0.310 l0；t=0.9 s 时刻v=0/1/2 m/s 流速下弹体迎流面上的空泡长度分别为0.287 l0/0.254 l0/0.240 l0，背流面上的空泡长度分别为0.254 l0/0.304 l0/0.370 l0。结果表明：随着流速的不断增加迎流面上空泡长度减小，背流面上空泡长度增加；相同流速下，弹体同一位置处迎流面空泡长度小于背流面空泡长度。当导弹尾部出筒后，弹尾附着气泡位置处存在与头部同样的压强变化规律，而弹体壁面不存在气泡的位置其迎流面和背流面的压强相差较小。因此，由于流速作用带来的迎流面压强大于背流面压强的区域，主要发生在导弹肩部空泡处和导弹尾部附着气泡处。

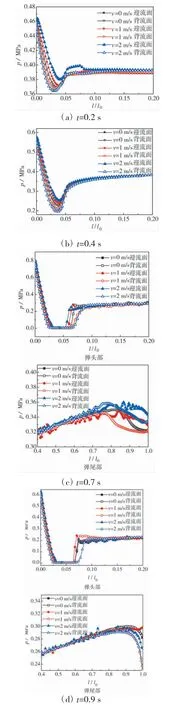
图6 不同时刻弹体壁面压强

3.3 弹道分析

图7 为不同流速下导弹出筒过程中x 向和y 向的质心位移曲线。由图可知，0.6 s 之前由于弹体位于筒内，受到筒内适配器的作用，所以在x 向和y 方向的位移几乎为0，而出筒后x 向的导弹位移主要由水的运动带来的冲击力引起，y 方向存在的微小位移是由筒盖的不对称以及水速共同作用。由于x方向为水流方向，因此，该方向导弹的位移要明显大于y 方向的位移。随着水流速度的增加，在越过筒盖区域后，弹体沿着x 正方向的位移逐渐增加。在本文研究的水流速度范围内，由于速度相对较小，导弹距离筒口10 m 范围内，x 向和y 向所产生的位移均较小。

图7 导弹弹道变化

4 结论

结合动力源入口压强变化和均压气体影响，基于混合多相流模型、RNG k-ε 湍流模型、Singhal 全空化模型耦合弹体运动开展了水速对弹体出筒阶段流场和弹道的影响。

1）分析了3 种流速下出筒阶段筒口气泡和肩部空泡变化规律，获得筒口气泡在混合介质与水相互作用下经历了膨胀、收缩和断裂变化过程，流速引起了筒口气泡的不对称，产生弹体在水流方向的偏转。

2）流速的增加引起迎流面上空泡长度减小，背流面上空泡长度增加；相同流速下弹体同一位置处迎流面空泡长度小于背流面空泡长度。