基于Fuzzy-AHP 的舰载反鱼雷武器系统安全性评估方法*

侯宝娥，田恒斗，高 阳

（解放军91439 部队，辽宁 大连 116041）

0 引言

舰载反鱼雷武器系统（以下简称“系统”）各设备在舰上分布位置不同、作战涉及因素众多、使用环境复杂，因此，对其安全性影响的因素不确定更不易量化。要科学、客观地对系统安全性进行评估，评估指标体系的确定、评估方法的选取十分重要。本文提出一种层次分析法和模糊综合评估法相结合的评估方法，既解决了指标因素多层次问题，又克服了评估过程的随机性及专家主观上的不确定性，以保证系统安全性评估的全面性、科学性。

1 评估方法介绍

层次分析法（Analytic Hierarchy Process，AHP）［4］是美国匹兹堡大学教授、运筹学家T.L.Saaty 提出的，是一种定量分析和定性分析相结合的、层次化、系统化的分析方法，把复杂的问题分解成有序的递阶层次结构，通过构造判断矩阵，确定层次中诸因素的相对重要性，常用于多属性问题中权重的确定。其分析过程如图1 所示。

图1 层次分析法流程示意

模糊综合评估法（Fuzzy Compositive Evaluation，FCE）［3］是美国自动控制学科专家Zadeh 教授提出的，解决模糊的、难以量化的、非确定性的问题，是一种基于模糊论的综合评估方法，可以根据模糊论的隶属度理论将定性评估转化成定量评估，即针对受到多种因素制约的事物，利用模糊论对其作出一个总体的评估。

考虑系统的作战使用特性及影响其安全性因素的多层次、复杂性，本文提出采用层次分析法确定系统安全性评价的指标体系、权重向量等，采用模糊综合评判法计算指标体系各层的评估结果，最终得到系统的安全性评估结果。

2 系统Fuzzy-AHP 安全性综合评价模型的建立

2.1 系统安全性评价指标体系的建立

评价指标体系是进行系统安全性评估的依据，科学全面地确定指标体系对评估结果有重要的作用。分析反鱼雷武器系统的组成、使用环境及作战流程，依据系统安全性设计要求及方案，确定影响系统安全性的因素主要包括武器安全性、武器发控安全性、电气安全性及软件安全性4 个方面，因此，建立系统安全性评价指标体系如图2 所示，安全性评价各指标因素分为目标层、准则层和指标层。

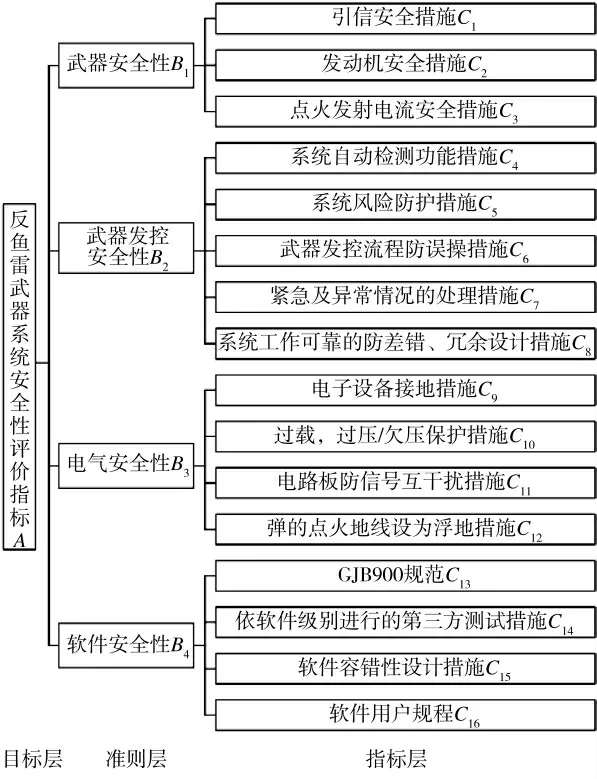
图2 反鱼雷武器系统安全性评价指标体系

2.2 系统综合评价因素集和评语集的确定

2.2.1 确定因素集

评估对象评估因素的集合称为因素集，表示为U={u1，u2，…，un}。确定因素集是模糊综合评判的第一步，也是重要的环节，在分析影响因素的过程中，通常采用AHP 法的思想，将因素考虑周全，并按照一定的属性关系进行层次的划分，从而实现多级的模糊综合评判。

系统的因素集即为其评价指标体系的准则层和指标层。

2.2.2 确定评语集

不同模糊评价的集合（如优、良、中、差等）称为评语集，评语级别由实际情况确定，表示为V={v1，v2，…，vm}。

确定系统安全性评价的评判等级为4 级：v1表示很安全，v2表示安全，v3表示基本安全，v4表示不安全，记为模糊评语集V=（v1，v2，v3，v4）。

2.3 系统安全性评价指标权重的确定

在系统安全性评价指标中，每个因素指标对系统安全的影响程度是不同的。为了恰当地表示出各个因素的影响程度，需要对各因素赋予相应的权重值。本文采用层次分析法来确定指标的权重。

2.3.1 构造判断矩阵

分别对同一层次的安全性评价指标进行两两比较，构造出各层次的所有判断矩阵，从而将定性的因素定量化。构造两两比较判断矩阵时，评价者需要比较两个因素哪一个更重要、重要多少，并对重要多少赋予一定的数值，Saaty 给出的重要性级别标度及其取值如表1［4］。

表1 重要性级别标度定义

由以上两两比较的方法，得出各层次的判断矩阵如下：

采用方根法［4］计算该判断矩阵的最大特征根max及其对应的特征向量W，具体计算步骤如下。

1）判断矩阵的元素按行相乘：

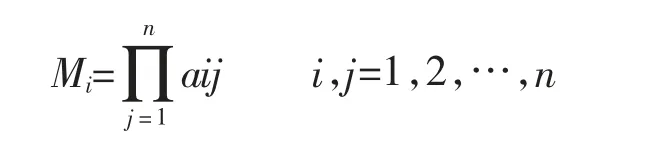
2）所得的乘积分别开n 次方：

3）将方根向量正规化，即得特征向量W：

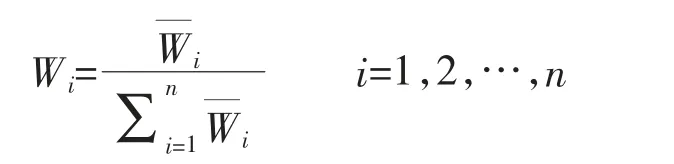
所得到的W=［W1，W2，…，Wn］T即为所求特征向量。

式中，（AW）i为向量AW 的第i 个分量。

2.3.2 检验判断矩阵的一致性

计算判断矩阵的一致性指标CI，定义

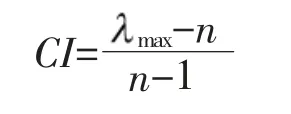
当CI=0 时，判断矩阵具有完全一致性；CI 越大，一致性越差。

对于一阶、二阶判断矩阵，通常满足一致性；当阶数大于2 时，采用概念“判断矩阵的随机一致性比例（记为CR）”来评价矩阵的一致性。

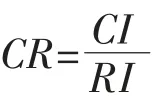
表2 平均随机一致性指标RI 值

当CR≤0.10 时，判断矩阵具有满意的一致性，当CR＞0.10 时，需要对判断矩阵进行调整。

判断矩阵满足一致性，则确定特征向量W 为该层次的权重。

2.4 模糊综合评估结果的计算

2.4.1 建立模糊评估矩阵

进行单因素评判，建立因素论域和评语论域之间的模糊关系矩阵为：

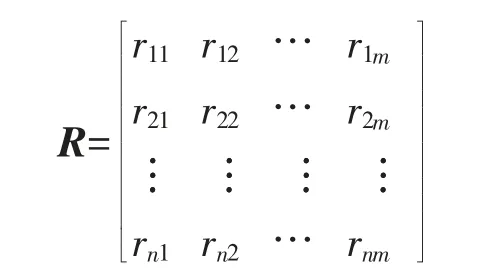
式中，rij为U 中因素ui对应V 中等级γj的隶属关系。

此矩阵可以视为因素集U 到评语集V 之间的一种模糊映射关系。

2.4.2 计算综合评估结果

为了保全评判中尽可能多的信息，本文采用加权平均型算子模型进行模糊综合计算。评估结果计算式为：

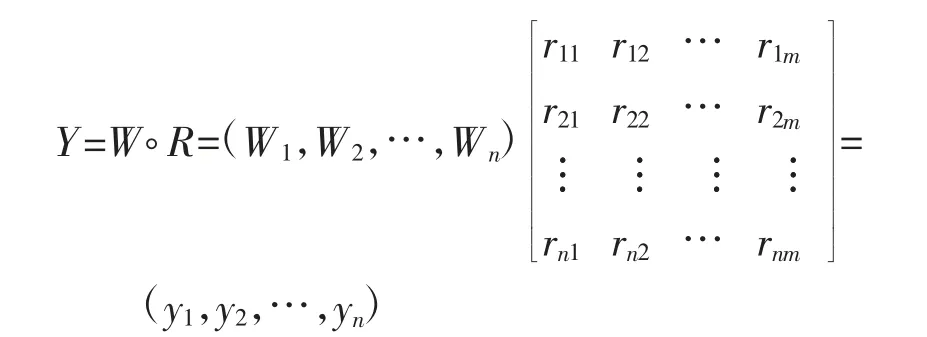
把位于最底层（第n 层）得出的评估结果合成作为上一层（第n-1 层）的模糊评估矩阵，以此计算该层评估结果，依此方法计算直至评估体系最顶层。

此处评价对象为反鱼雷武器系统安全性，是对系统定性的评价，按最大隶属度原则，取最顶层评估结果的max{y1，y2，…，yn}来确定被评判对象对应的评判等级。

3 系统安全性评价方法验证

3.1 计算指标权重

根据反鱼雷武器系统安全性评价指标体系，在对系统安全性定性检查、系统故障假设分析和专家试验现场咨询等的基础上，对系统安全性指标各层中因素进行两两比较，获得同级影响因素之间的重要度比值。假设准则层因素重要度比值如表3 所示。

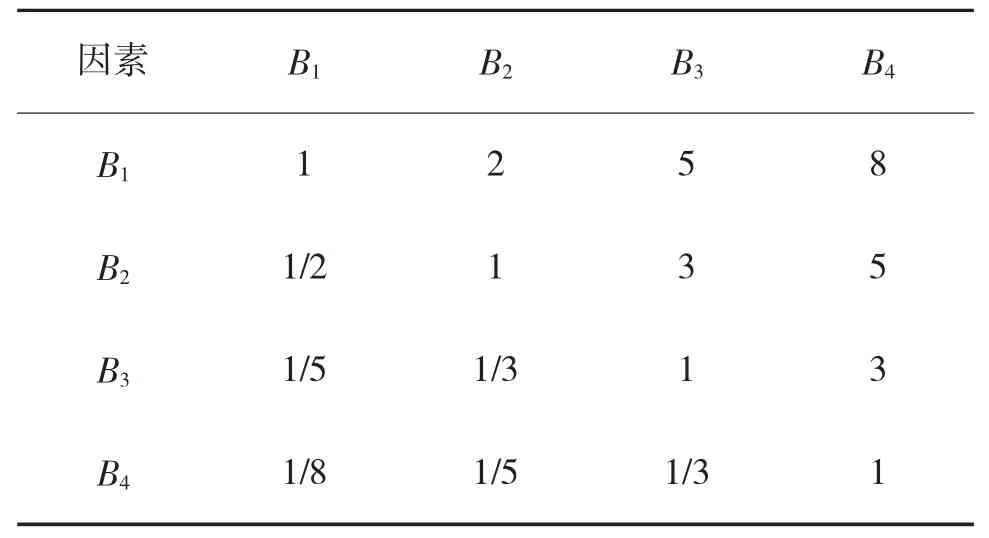
表3 反鱼雷武器系统安全性（A）

采用方根法求得系统安全性评价指标判别矩阵的特征向量W：

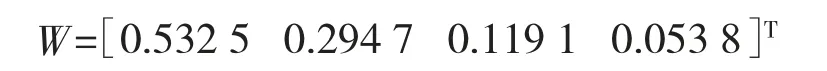
矩阵的一致性指标CI =0.072 865，CR=0.081＜0.1。

所以该矩阵满足一致性，其准则层系统安全性评价指标权重为：

W=［0.532 5 0.294 7 0.119 1 0.053 8］

同理，可得出指标层各因素权重如下：

武器安全性的权重：W1=［1/3 1/3 1/3］

武器发控安全性的权重：

W2=［0.056 4 0.109 0 0.233 4 0.492 2 0.109 0］

电气安全性的权重：

W3=［0.432 4 0.094 9 0.144 1 0.328 6］

软件安全性的权重：

W4=［0.617 9 0.265 9 0.072 7 0.043 6］

3.2 系统安全性评价

请若干专家，通过打分确定影响系统安全性的各因素被评定为评语集V 中各评语级别的隶属度，形成模糊评估矩阵，与所求各层的权重一并建立系统安全性评估因素体系，如表4 所示。

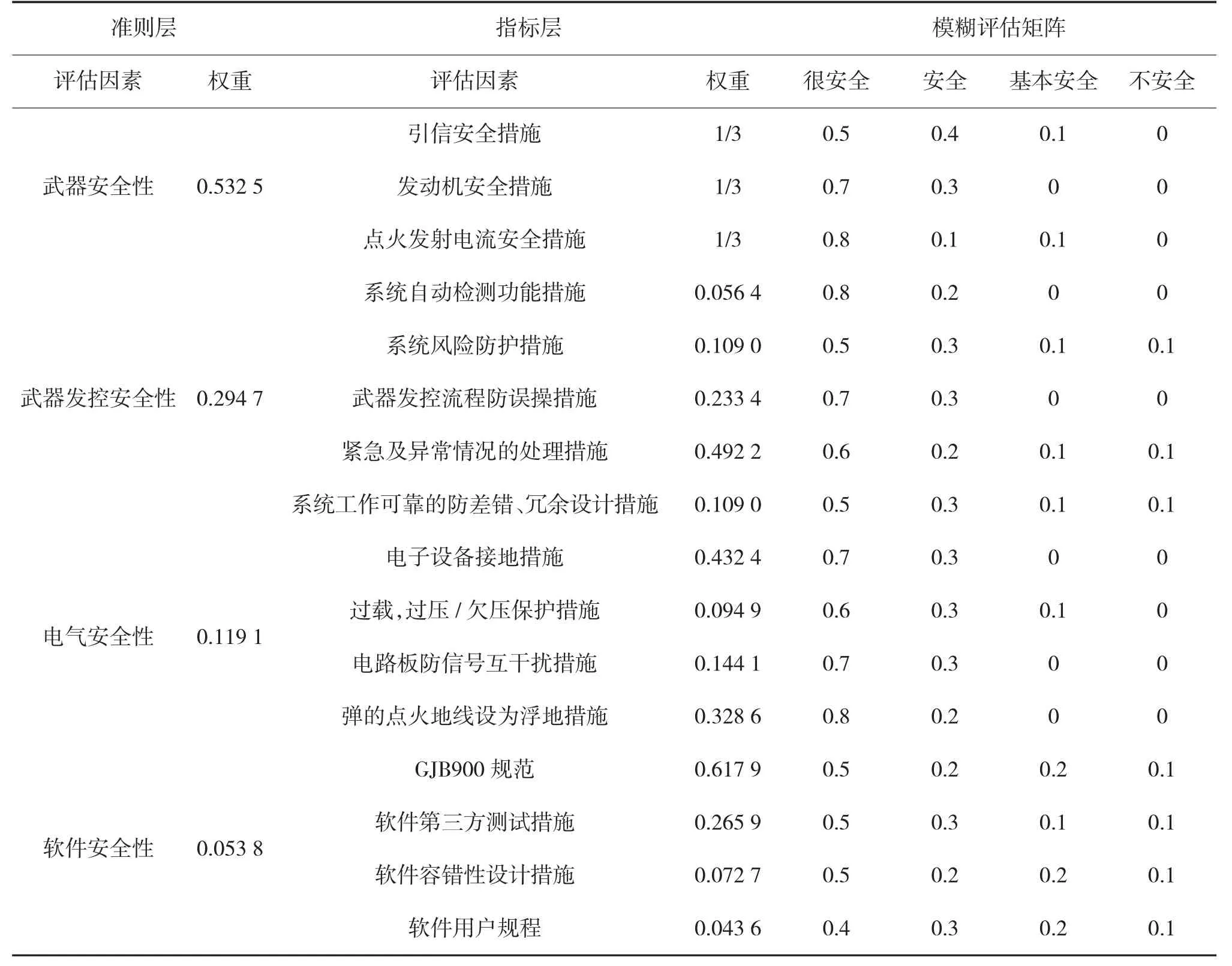
表4 反鱼雷武器系统安全性评估因素体系

以评估因素——引信安全措施为例。假设：请10 个专家对其隶属度进行评定，其中有5 人认为是很安全的，4 人认为是安全的，1 人认为基本安全，0人认为不安全，则引信安全措施的隶属度集为（0.5，0.4，0.1，0）。同理，可得发动机安全措施的隶属度集和点火发射电流安全措施的隶属度集，最终得出准则层武器安全性的模糊评估矩阵R1。

依此方法，可得准则层武器发控安全性的模糊评估矩阵R2，电气安全性的模糊评估矩阵R3，软件安全性的模糊评估矩阵R4。

3）由公式Yk=Wk·Rk，k=1，2，3，4 计算准则层各因素的综合评估结果如下：

Y1=W1◦R1=［0.666 7 0.266 7 0.066 7 0］

Y2=W2◦R2=［0.612 8 0.245 1 0.071 0 0.071 0］

Y3=W3◦R3=［0.723 4 0.267 1 0.009 5 0］

Y4=W4◦R4=［0.495 7 0.231 0 0.173 4 0.100 0］

可得目标层模糊评估矩阵R=［Y1Y2Y3Y4］T。

目标层系统安全性综合评估结果为：

Y=W◦R=［0.648 5 0.258 4 0.066 8 0.026 28］

4）按最大隶属度原则，取max（y1，y2，y3，y4）=0.648 5，对应评语集V=（v1，v2，v3，v4）中“v1很安全”即为反鱼雷武器系统安全性的评价结果。

以上通过假设各层次因素重要度比值、各因素评语级别隶属度，验证了本文提出的系统安全性评估方法的可行性科学性。

4 结论

本文提出基于Fuzzy-AHP 的安全性评估方法，能够对使用环境不确定且复杂、指标体系多层的反鱼雷武器系统的安全性作出科学合理的评估。该评估方法将科学计算与专家经验相结合，保全了评判中尽可能多的信息，提高了评估结果的可信性，此方法也可推广应用于武器系统其他性能的评估。