基于量测噪声方差估计的GM-CBMeMBer 算法

董 青，胡建旺，吉 兵

（陆军工程大学石家庄校区，石家庄 050003）

0 引言

在目标跟踪过程中，由于电磁环境、温度和其他因素影响，量测噪声概率分布难以准确获取。传统的多目标跟踪算法常假设噪声统计特性先验已知，然而真实场景下，量测噪声时变且难以准确获取。

为解决这一问题，专家学者提出在进行多目标跟踪的同时在线估计噪声统计特性。文献［4］提出将状态噪声的概率分布视为逆伽马分布。SAGE等［5］提出最优的自适应贝叶斯估计方法，但该算法在工程上难以实现。为增强算法的工程有效性［6-7］，进一步提出可同时估计噪声的均值和方差次优算法（Sage-Husa 自适应算法），但该算法存在不能同时估计状态噪声和量测噪声的统计特性的局限性。此外这些在线估计噪声的自适应算法的应用对象均为单目标。

近年来，专家学者的视线逐步转移到噪声统计特性未知的多目标跟踪系统中。文献［8-9］将变分贝叶斯方法和概率假设密度滤波相结合来实现对多目标进行跟踪。但该算法耗时较长且文献并未给出迭代终止条件或收敛参数的方法。文献［10］采用多模型估计方法修正噪声方差。针对时变量测噪声，梁荔等人提出有偏估计的思想实现噪声统计特性未知条件下的PHD 算法［11］。

为进一步扩展解决多目标跟踪系统中量测噪声统计特性未知问题的途径，本文基于GM-CBMeMBer 滤波算法［2-3］，提出量测噪声方差在线估计的多目标跟踪算法。针对量测噪声时变且未知的问题，引入遗忘因子增强算法的噪声敏感性，并采用协方差匹配方法监督滤波器发散情况，为修正跟踪发散问题，考虑采用有偏估计的方法修正量测噪声方差估计。仿真实验验证了改进算法的有效性。

1 问题描述

通常，离散状态空间中多目标跟踪系统的状态方程和量测方程可以描述为

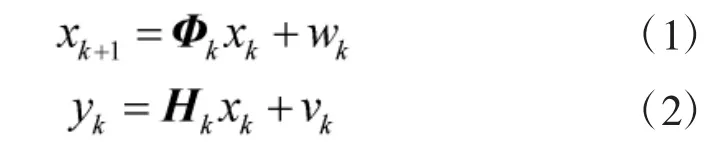
2 GM-CBMeMBer 滤波算法

基于随机有限集的CBMeMBer 滤波器将目标集合当作全局目标，传感器输出的量测集合作为全局量测。随机有限集理论将多目标跟踪问题转变为并行单目标跟踪问题，跳过了量测到航迹的显式关联问题，极大降低了计算复杂度。下面给出GM-CBMeMBer 的滤波过程。

1）预测

设k-1 时刻的多目标密度为：

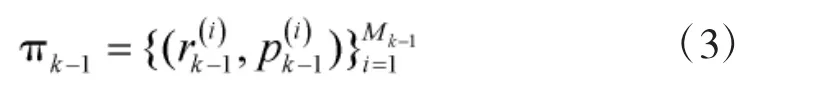
则k 时刻预测的多目标密度为：

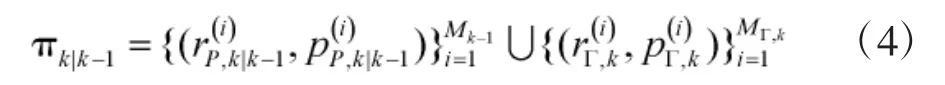
其中

2）更新

已知k 时刻预测的多目标密度描述：

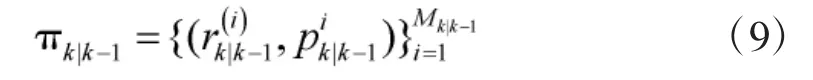
则其k 时刻更新的多目标密度可近似表示为：

其中

3）剪枝合并

与GM-PHD 类似，GM-CBMeMBer 算法高斯项的个数会随着时间的推移无限增加，为减少高斯项个数，需要对假设轨迹进行剪枝融合操作：设置轨迹存在概率门限，对存在概率低于门限值的轨迹进行删除，高斯项的剪枝合并具体与GM-PHD 类似。

4）状态估计

3 改进算法

GM-CBMeMBer 滤波算法的滤波过程依赖于系统模型。当系统模型建立不当或噪声的真实统计特性与预设值偏离程度较高时，滤波算法会出现稳态误差增大，甚至发散的现象。文献［11］基于GM-PHD 的高斯混合实现框架，采用Sage-Husa 次优无偏估计的极大后验算法，对跟踪系统中的噪声（过程噪声和量测噪声）统计特性进行在线估计，取得了较好的效果。

本文利用Sage-Husa 估计器对量测噪声进行估计，并引入协方差匹配方法对滤波器的发散情况进行判断，若滤波器发散则采用有偏估计方法来修正状态噪声协方差矩阵。

3.1 改进的量测噪声估计器

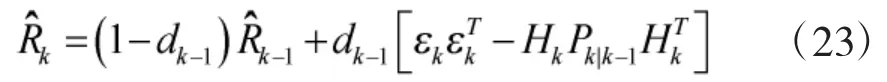
式（23）采用相减算法以满足无偏估计的要求。但该操作易使量测噪声方差估计值失去正定性，致使滤波发散。为解决这一问题，本文首先采用假设检验判断滤波是否发散，H0表示未出现发散现象，H1表示出现发散现象。检验统计量为：

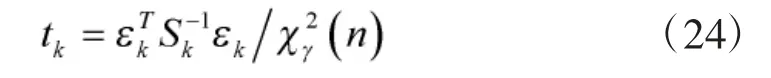
若未出现发散，则tk≤1，反之，tk＞1，滤波其发散，失去正定性。此时采用有偏估计式（25）来修正估计值。

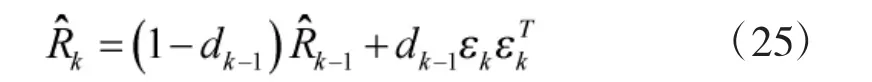
经实验验证，加权系数恒dk-1≤1，只要初始量测噪声方差阵正定，则通过式（25）修正的量测噪声方差阵也为正定矩阵。

3.2 算法实现步骤

1）预测

其中，通过式（5）、式（6）计算。与标准算法的预测步骤相比，改进算法同时递推量测噪声统计特性，该变量可由式（23）计算得出。

2）假设检验

利用式（24）判断tk，若tk＞1，则转入式（25）。

3）更新

更新的多伯努利随机有限集为：

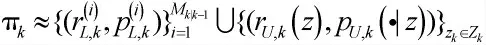
上式各变量可通过式（11）～式（21）计算得出，同时传递量测噪声的统计特性。

4）剪枝合并与状态估计

具体操作与第2 节相同。

4 仿真实验

本文基于多机动目标场景进行仿真实验，仿真软件为MATLAB 2013b，首先介绍仿真实验参数，其次对仿真结果进行分析。

4.1 实验参数设置

4.2 仿真结果分析

实验1：量测噪声方差未知且固定

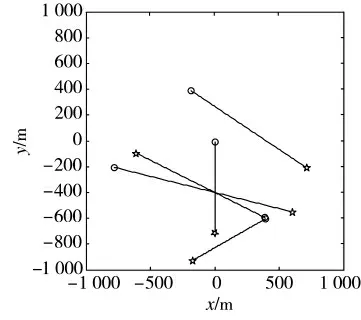
图1 目标真实轨迹

图2、图3 分别给出了标准算法和改进算法x和y 方向的位置估计。由图2 可知，由于量测噪声方差和真实量测噪声方差不符，标准GM-CBMeMBer算法跟踪精度差。由于误差累积，在尾部时刻存在目标丢失现象。在图3 中，由于改进算法不需要量测噪声先验信息，采用在线估计方法估计量测噪声方差，因此，该算法的量测噪声方差估计更贴近真实量测噪声统计特性。与标准算法相比，改进算法具有较高的跟踪精度。

图2 量测噪声方差未知条件下的GM-CBMeMBer 算法的位置估计

图3 量测噪声方差未知条件下的改进算法

为验证算法有效性，本文采用最优子模式分配［13］（Optimal Subpattern Assignment，OSPA）距离作为算法性能的评价指标。其中距离敏感性参数p=1，截断距离c=100。图4 为两种算法经过50 次蒙特卡洛仿真的OSPA 距离对比图。由下页图4 可知，改进算法的OSPA 距离明显小于量测噪声未知条件下的GM-CBMeMBer 算法。在起始时刻，改进算法的OSPA 距离明显高于量测噪声方差已知的GM-CBMeMBer 算法，这是由于起始时刻量测数据不充分造成的；在后续时刻，改进算法的跟踪性能趋于稳定，与量测噪声方差已知的GM-CBMeMBer算法相近。

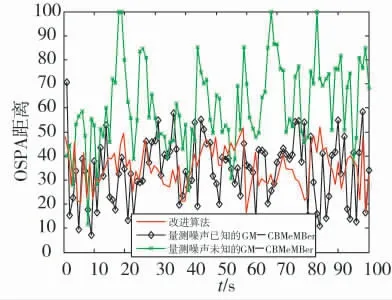
图4 OSPA 距离对比图

实验2：量测噪声未知且时变

图5 给出了实验2 真实量测噪声变化图，表示传感器突然受外界强干扰，而量测噪声标准差出现阶跃变化现象。此时改进算法的遗忘因子b 取值为0.975。

图5 量测噪声标准差变化图

由图6 可知，由于标准算法的量测噪声参数与实际量测噪声不匹配，出现时变现象，标准算法的OSPA 距离明显大于改进算法。在30 s 和60 s，量测噪声方差出现跳变，标准算法的误差不同程度地增大，但改进算法也能较好地保持跟踪性能，这是因为噪声方差估计过程中使用了遗忘因子，降低了陈旧信息对当前时刻的影响。

5 结论

针对实际目标跟踪系统中量测噪声统计特性未知且存在时变现象的问题，本文提出一种在线估计量测噪声方差的GM-CBMeMBer 算法。仿真结果表明，在多目标跟踪场景下，当量测噪声真值与先验不匹配时，标准的GM-CBMeMBer 滤波算法存在漏检，甚至目标丢失的现象，而改进算法能稳定地进行目标跟踪，更加适用于真实场景。

图6 OSPA 距离对比图