三个代数不等式链的几何证明

首都师范大学数学科学学院(100048) 田朋朋

文[1]在圆中建立了四类平均数的几何模型.文[2]以三角形为基础,证明了共角的四个三角形共角所对应的边是四类平均数的几何模型,但并未给出对应边详细的几何作图方法.文[3]以直角三角形为基础,对四类平均数图解进一步探究,得到两正数a,b的五个平均值的不等式链.文[4]以第七届国际数学教育大会会徽图案模型为基础,给出含六个平均值的不等式链的一种几何解释.本文以梯形为基础,首先证明了梯形内平行于上下底边的六条平行线段是六类平均数的几何模型,得到一条含六类平均数的不等式链：

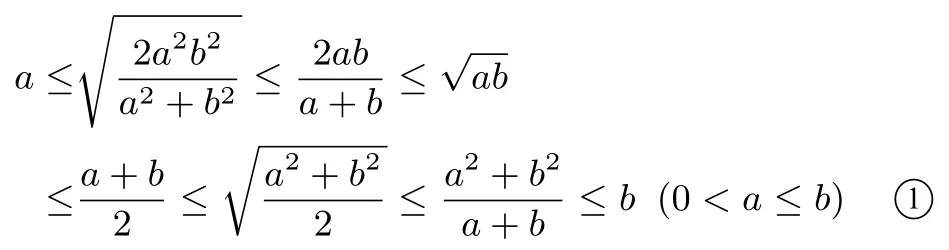
当且仅当a=b时,等号成立.

然后根据其中五条平行线段分梯形面积成比例的性质,得到两条新的不等式链：

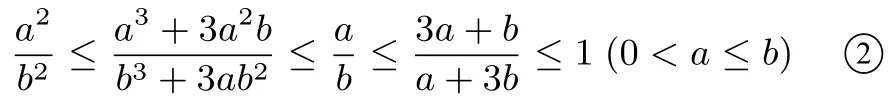
当且仅当a=b时,等号成立.

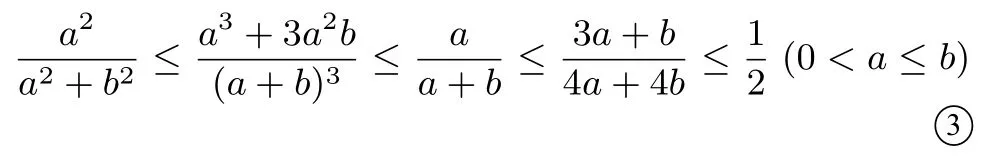
当且仅当a=b时,等号成立.

下面就给出不等式链①的几何模型以及两条新不等式链②和③的探究过程.

1.几何模型

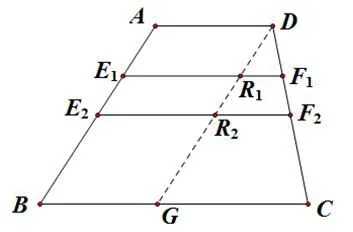
图1

引理如图1,在梯形ABCD中,AD//BC,AD＜BC,E1F1//E2F2//BC.若AE1＜AE2,则E1F1＜E2F2.

证明从略.

如图2至图6,梯形ABCD中,AD//BC,AD＜BC,延长BA,CD交于点M,设AD=a,BC=b,则AD,BC边上的高可分别设为MG=ka,MN=kb,(k＞0).

如图2,连接AC,BD交于点O,过O作直线E1F1//BC,交AB,DC于E1,F1.可求得E1O=F1O=则设E1F1与MN交于点N1,则解得MN1=.

如图2,取AB的中点E3,CD的中点F3,连接E3F3,则E3F3=.设E3F3与MN交于点N3,则MN3-MG=MN-MN3,解得MN3=.

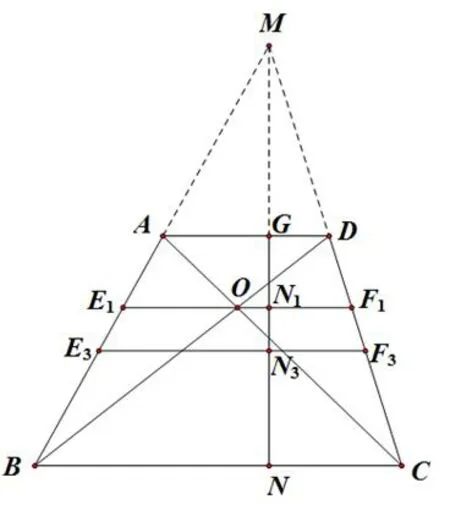
图2

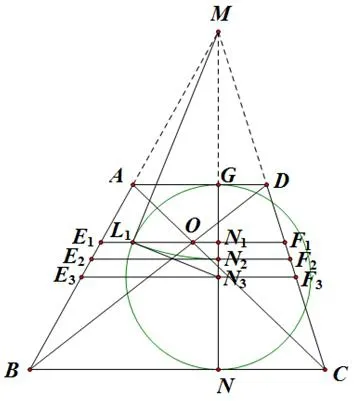
图3

如图3,以N3为圆心,GN3为半径作圆N3交E1F1于点L1,以M为圆心,ML1为半径画弧交MN于点N2,过N2作直线E2F2//BC,交AB,DC于E2,F2.

此时,连接N3L1,则N3L1=GN3=,N1N3=MN3-MN1=根据解得所以又即所以

另外,由MG=ka,MN=kb,ML1=可知满足即若连接GL1,NL1,则△MGL1∽△ML1N,可推出∠ML1N3=90°.因此,ML1为圆N3的切线,且容易推出有：GN1＜GN2＜GN3,即有：E1F1＜E2F2＜E3F3.

此 时,S梯形AE2F2D=因此,平行线段E2F2分梯形ABCD上下面积比为.

如图4,设圆N3交E3F3于点L2,以M为圆心,ML2为半径画圆弧交MN于点N4,过N4作直线E4F4//BC,交AB,DC于E4,F4.则有GN3＜GN4,即E3F3＜E4F4.且有N3L2=,根据解得ML2=,所以MN4=又根据,即,解得E4F4=.

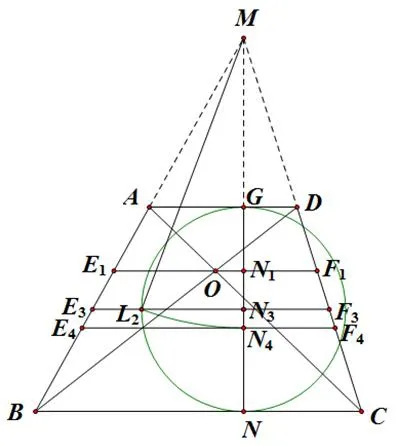
图4

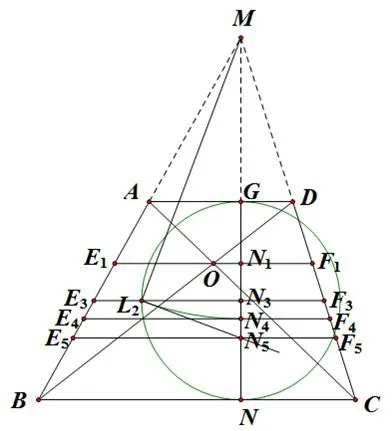
图5

如图5,在图4的基础上,过点L2作ML2的垂线交MN于点N5,过N5作直线E5F5//BC,交AB,DC于E5,F5.则有GN4＜GN5,即E4F4＜E5F5.因为△ML2N5为直角三角形,所以有即,又根据即解得

如图6,设ML2交圆N3于点L3,以M为圆心,ML3为半径画圆弧交MN于点N0,过N0作直线E0F0//BC,交AB,DC于E0,F0.因为ML1为圆N3的切线,ML2为圆N3的割线,根据圆的切割线定理可得即所以MN0=又根据所以E0F0=.此时,

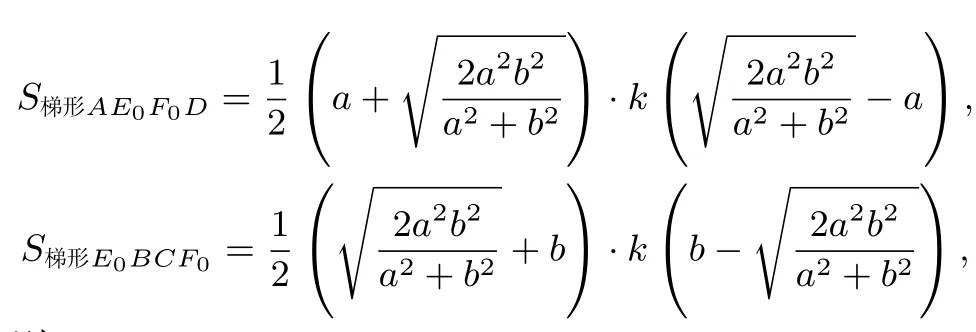
则

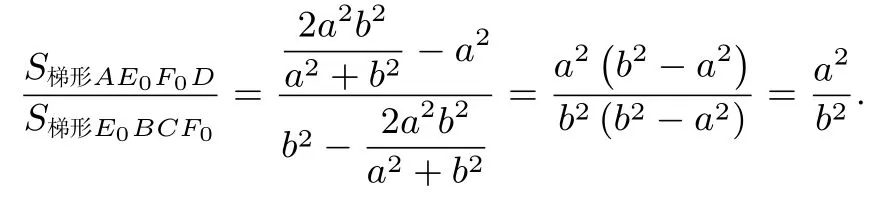
因此,平行线段E0F0分梯形ABCD上下面积比为.

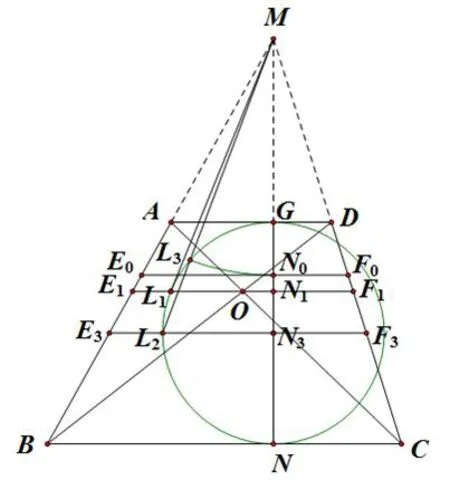
图6

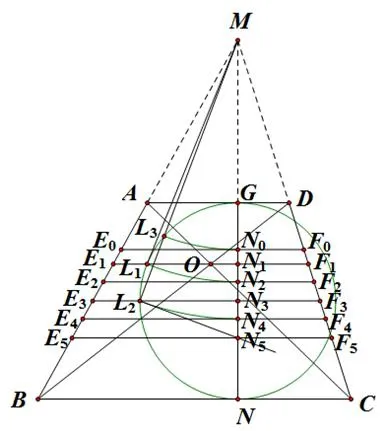
图7

现将六条平行线段E0F0,E1F1,E2F2,E3F3,E4F4,E5F5在同一梯形ABCD中画出,如图7所示,结合引理可得：AD＜E0F0＜E1F1＜E2F2＜E3F3＜E4F4＜E5F5＜BC,即a≤≤b(0＜a≤b).当且仅当a=b时,等号成立.

即在排列次序上,几何平均值处于调和平均值与算术平均值的中间位置;几何平均值也处于平方平均值与之间的位置;平方平均值处于算术平均值与之间的位置.

2.两条新的不等式链

如图7所示,对于其中的五条平行线段EiFi(i=0,1,2,3,4),随着i的增大,梯形AEiFiD的面积在逐渐增大,而梯形EiBCFi的面积在逐渐减小.所以,随着i的增大,的比值在逐渐增大.因此,可得不等式链：当且仅当a=b时,等号成立.

若设梯形ABCD的面积为S,梯形AE0F0D,AE1F1D,AE2F2D,AE3F3D,AE4F4D的面积分别为S0,S1,S2,S3,S4.则有

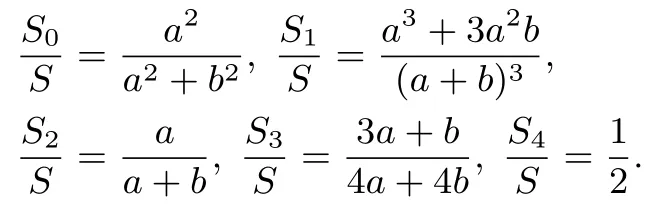
又因S0＜S1＜S2＜S3＜S4,则有不等式链：

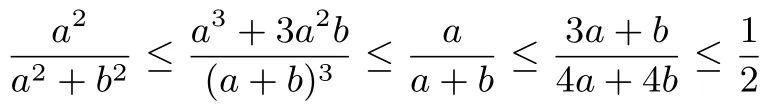
(0＜a≤b).当且仅当a=b时,等号成立.

3.体会

这样,就给出了不等式链①在梯形中的一个直观的几何解释,将比较六类平均数的大小转化为比较六条平行线段的长短,并且六条平行线段完全可以用尺规作图作出,体现了“数”与“形”结合的统一美,展示了数形结合的魅力.不等式链②和③的产生以比较梯形面积比值为基础,体现了从线段度量到面积度量的升华,为继续发现新的不等式链提供了方向.希望同学们进一步思考,给出不等式链更加直观的几何解释,继续找寻更加简明的不等式链.