动载荷作用下的轴颈涡动与滑动轴承瞬态油膜力耦合机制研究

李 强， 张 硕， 王玉君， 许伟伟， 王振波

(1. 中国石油大学(华东) 化学工程学院，山东 青岛 266580；2. 中国石油大学(华东) 储运与建筑工程学院，山东 青岛 266580)

不平衡量等动载荷可导致轴颈在滑动轴承静平衡位置附近产生涡动，进而对于高速机床等大型旋转机械的运行状态产生影响[1]。其中由于油膜自激导致的涡动频率一般略低于转速的一半，因此也常称之为“半速涡动”[2]。20世纪20年代，Newkirk等[3]将半速涡动的矛头指向滑动轴承以来，揭示在转子涡动过程中瞬态油膜力与轴颈涡动之间耦合作用机制一直是转子-滑动轴承领域的热点之一，随着研究的推进瞬态油膜力模型依次经历了线性化模型[4]、瞬态理论油膜力模型[5]、瞬态Reynolds方程模型[6]等。目前，线性化油膜力模型常用于小扰动下滑动轴承支撑的转子动力学分析[7]，当扰动增大时，油膜力的非线性效应逐渐增强[8]。而理论油膜力模型仅在部分条件下才能得到较为精确结果，因此常用于滑动轴承-转子系统的简化分析[9]。瞬态Reynolds方程模型由于忽略了惯性项等因素，其弊端也在不断显露[10]。

商用CFD(Computational Fluid Dymamics)软件在滑动轴承性能计算中的应用极大的促进了其性能预测和结构改进。目前，已经在稳态润滑性能的预测方面做了大量的工作，包括已经针对不同的轴承结构[11]、不同的润滑模型，如EHD(Elastohydrodynamic)模型[12]、THD(Thermohydrodynamic)模型[13]开了大量研究。采用动网格技术可将CFD在滑动轴承中的应用拓展至动特性计算方面，较早开始该方面研究的是Guo等[14]采用基于小扰动方法，以CFX-TASC为求解器计算了滑动轴承的动特性系数。随后，Gertzos等[15]基于FLUENT计算了非牛顿流体润滑作用下的转子的静平衡位置；熊万里等[16]采用类似方法计算了液体动静压轴承刚度阻尼；Cheqamahi等[17]将动网格技术用于求解静平衡位置，并与理论油膜力模型对比，发现吻合较好；孙丹等[18]在考虑轴颈涡动的情况下计算了滑动轴承的动特性系数。

但是上述基于CFD非线性油膜力研究仅限于静平衡位置求解或者小扰动下的动特性系数计算，这是由于在大扰动下滑动轴承等小间隙流场的瞬态计算中，如果采用传统的动网格模型，会由于网格质量过差导致计算发散或精度降低。因此瞬态CFD模型下轴颈涡动与滑动轴承瞬态油膜力之间的耦合作用机制，尤其是在不平衡量等动载荷作用下的研究尚不充分。为此，Li等[19]提出了一种结构化动网格模型，并进行了圆柱型滑动轴承的瞬态工作过程分析。

另外，试验和理论均已表明多油楔滑动轴承相对于传统圆柱形滑动轴承具有稳定性好[20-21]、温升小的特点[22]，相对于可倾瓦滑动轴承具有结构简单容易加工的特点，因而广泛应用于中小型涡轮增压机、汽轮机、发电机中[23]。但目前从多油楔滑动轴承轴颈涡动与瞬态油膜力之间的作用机制出发理解多油楔滑动轴承稳定性的研究鲜有报道。

本文针对上述不足，采用自行开发的变流域结构化方法建立了动载荷作用下圆柱形和多油楔滑动轴承的瞬态流固耦合计算模型，首先以圆柱形滑动轴承为例分析了油膜力与轴颈涡动的耦合作用机制，然后从非线性瞬态油膜力变化的角度直观揭示了多油楔滑动轴承优良稳定性的原因。

1 控制方程

1.1 基本控制方程组

基本控制方程组的通用形式为

(1)

式中：φ为通用变量；Γφ为广义扩散系数；Sφ为广义源项，取值如表1所示。

表1 通用控制方程中各符号的具体形式

1.2 空化模型

滑动轴承发散楔会引起油膜压力降低，进而导致气态润滑介质的出现，该气液之间的质量转移采用Singhal等[24]提出的“全空化模型”计算，如式(2)～式(3)。气液混合相的流动状态采用Mixture模型描述。

(2)

(3)

1.3 转子运动方程

本文主要讨论在不同的动载荷下轴颈涡动与油膜力之间的耦合作用机制，而与具体的转子系统无关，因此计算模型简化为一个滑动轴承上支撑一段旋转的轴，如图1所示。图中粗实线为圆柱形轴承和椭圆形轴承进油口和油槽，细虚线为三油楔滑动轴承进油口和油槽(椭圆轴承和三油楔轴承在圆柱形轴承基础上增加了楔形度，图中未表示)。

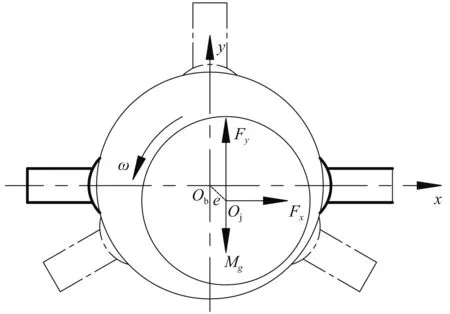
图1 转子计算示意模型Fig.1 Calculation model of rotor

轴颈运动方程为

(4)

式中：M为转子质量；Fx，Fy为水平和竖直方向油膜力分量；e为偏心距。

通过改变偏心距e，可以得到不同的偏心动载荷，进而可以进行不同动载荷作用下的轴颈涡动与滑动轴承瞬态油膜力耦合机制研究。

2 计算模型及方法

2.1 物理模型及边界条件

本文采用滑动轴承轴承为径向供油，轴端出油的径向滑动轴承，油槽采用轴向凹槽，并以载荷作用线为对称线进行开槽。三维模型如图2所示。滑动轴承具体结构尺寸、润滑介质和运行参数如表2所示。多油楔滑动轴承(椭圆轴承、三油楔轴承)相对于圆柱形滑动仅在结构上改变了楔形度，以增加预负荷系数。边界条件为压力入口和压力出口，轴颈内壁面为旋转壁面，其余为固定壁面，且所有壁面无滑移。

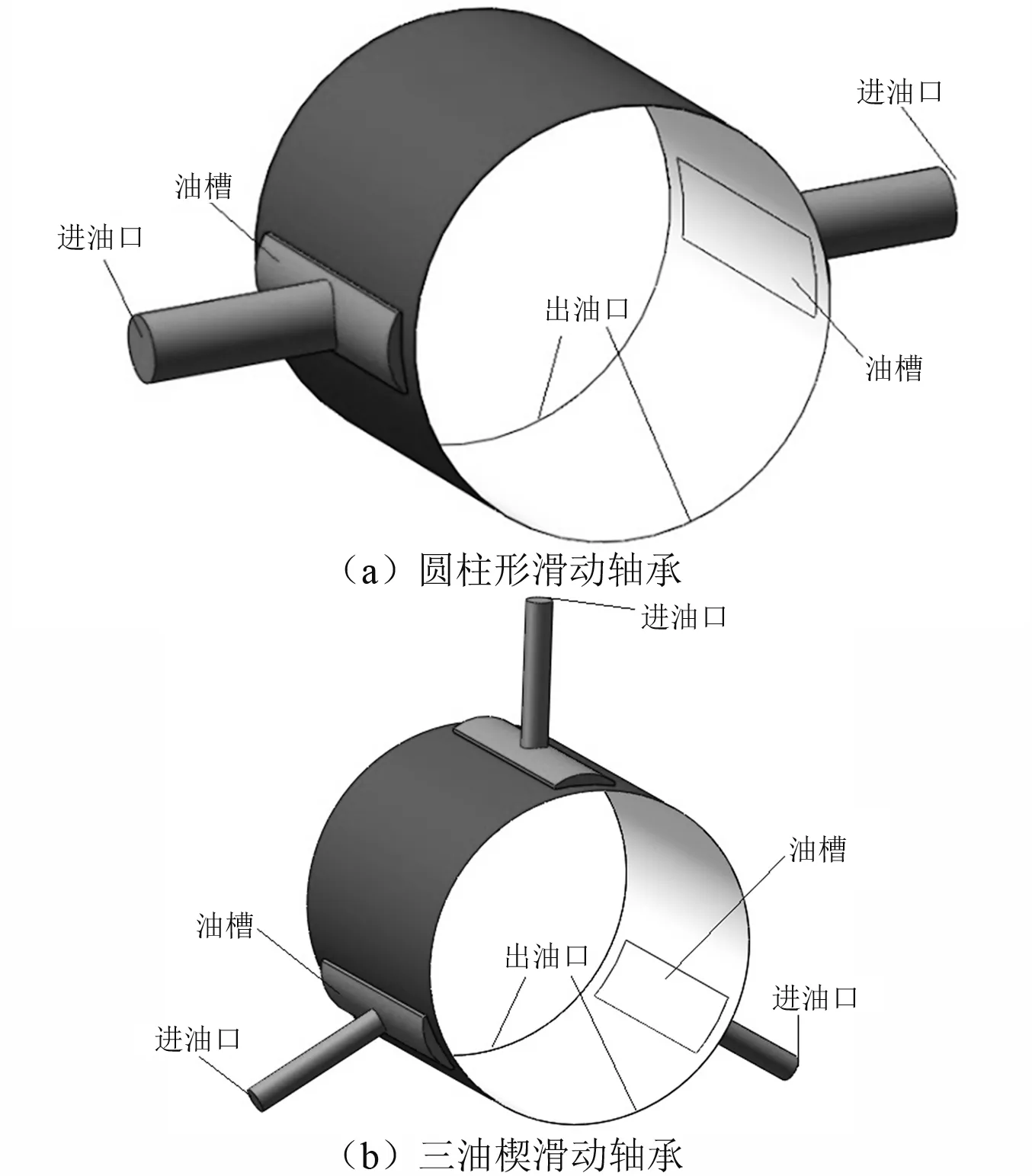
图2 三维模型Fig.2 3D geometry models

2.2 分流域结构化动网格方法

Li等提出了一种圆柱形轴承的结构化动网格技术，通过UDF(User Defined Function)实现了油膜间隙内网格的均匀排列进而保证了计算过程中的网格数量和网格质量，相对于圆柱形滑动轴承，多油楔滑动轴承可视为由多个部分圆柱形油楔的拼接，因此可在该基础上通过提前判断网格节点所处流域对应的油楔，并

表2 计算参数

在每一个油楔内采用圆柱形滑动轴承动网格更新技术。更新后的网格如图3所示(以三油楔滑动轴承为例)。

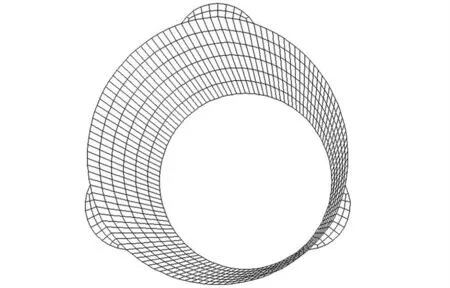
图3 更新后的网格模型Fig.3 Mesh model after grid updating

2.3 计算过程

基于上述动网格技术，通过UDF程序交换流体域和固体域之间的计算结果，从而实现滑动轴承与转子系统的流固耦合计算，计算过程如图4所示。首先，采用SIMPLE算法进行稳态初始流场计算，并将稳态计算结果作为初始条件采用PISO(Pressure-Implicit with Splitting of Operators)算法开始非稳态计算。通过积分油膜压力得到轴承在该工况下的承载力Fx，Fy，并作为边界条件导入转子动力学方程，利用Newmark积分法求解动力学方程可以得到该时刻轴颈的几何位置(Δx，Δy)，在FLUENT中借助自行开发的动网格程序实现轴颈该位移量的移动，在更新后流场网格的基础上进入下一时间步的计算，以此循环更新直至达到计算要求。

2.4 准确性验证

由于瞬态油膜力和轴颈涡动轨迹的试验测量受限较多，且本文重点应验证所提出的瞬态油膜力模型是否合理。因此通过将运动方程中的偏心距e置为0，即不考虑动载荷的影响，轴颈受到稳定外载荷和瞬态油膜力的作用。以轴颈最终稳定平衡位置的偏心率与文献[25]试验结果进行对比(见表3)，文献[25]中的转子模型与本文计算模型相同，均为等截面轴。可以看出两者相差均在2.5%以下，可以说明计算方法的准确性和有效性。

图4 转子-轴承系统流固耦合计算流程图Fig.4 Fluid-solid coupling calculation process of rotor-journal bearings system

表3 模拟结果与试验结果的对比

3 圆柱形滑动轴承

在仅考虑油膜自激的前提下，如果在轴颈涡动一周内，油膜力做功为负，即

(5)

则系统是稳定的。线性化油膜力理论认为在静平衡位置附近油膜力可作如下展开

(6)

式中：kij和cij分别为刚度系数和阻尼系数，根据方向不同i，j分别取x，y。

设轴颈中心围绕静平衡位置作稳态的椭圆运动，其运动方程可以表述为

(7)

将式(6)，式(7)代入式(5)，可以得到

Wf=π(kxx-kxy)XYsinβ-πω(cxy+cyx)XYcosβ-
πωcxxX2-πωcyyY2<0

(8)

所以线性油膜力模型通过计算刚度和阻尼系数来判断系统的稳定性，但是这一理论尽在小扰动情况下成立。当动载荷较大时，其预测结果与实际相差较远。

理论油膜力模型通过在长轴承或者短轴承假设下，积分求解简化后的Reynolds方程获得瞬态油膜力，而瞬态Reynolds方程模型通常采用有限差分或者有限元的方法直接计算Fx，Fy，稳定性由式(5)判断。但是由于Reynolds方程是由式(1)忽略惯性效应等而得来，所以随着转子转速升高，其弊端也在不断显露。

本文建立的瞬态CFD模型可以很好的弥补上述缺陷，为了分析动载荷下轴颈涡动与瞬态油膜力之间的关系，首先将计算获得的Fx，Fy，按图5进行分解，获得径向油膜力和切向油膜力(为方便作图，规定切向油膜力与轴颈涡动方向相反时为负，径向油膜力指向曲率中心为负)。

图5 轴颈中心涡动时油膜力分量关系图Fig.5 Oil film force components during whirling

则，式(5)可以简化为

(9)

所以当切向油膜力为负时，有助于转子系统保持稳定涡动，而径向油膜力则充当弹性恢复力，为轴颈提供油膜刚度。

为了充分理解油膜力和轴颈涡动轨迹之间的关系，下面以经典圆柱形滑动轴承为例分析了不同动载荷作用时的瞬态CFD模型油膜力与涡动轨迹之间的变化关系。从轨迹变化图6可知，当系统发生半频涡动后，随着动载荷的增大，涡动轨迹的内圆在增大，当增加到80 μm的时候，内外两轨迹基本重合，半频涡动消失，只剩下基频涡动。

轴颈涡动过程中的切向瞬态油膜力、径向瞬态油膜力如图7～图8所示。从图7和图8可知，当动载荷较小(e=50 μm)时，轴颈涡动轨迹比较小，收敛楔形成的油压比较小，因此得到的径向和切向油膜力都较小，而正径向力的出现使得支撑刚度不足，从频谱图(见图

图6 轴心轨迹随动载荷的变化过程Fig.6 Journal orbits with respect of eccentricity

9)可以看出小动载荷下油膜力存在明显半频，进一步说明轴颈的半频涡动是由于油膜力自激导致；随着动

载荷的增大，轴心涡动轨迹也随之增大，使收敛楔形成的动压变大，径向油膜力逐渐全部变为负值，使系统的支撑刚度变大，而切向油膜力始终起阻尼作用，而且这种阻尼作用随着动载荷的增大而增大，在大的支撑刚度和始终起阻尼作用的油膜切向力的作用下，半频涡动分量被完全抑制，只剩下工频涡动。为验证上述分析结果，对e=150 μm下得到的时域信号进行傅里叶变化，如图10所示。从图10可知，在位移开始阶段，半频涡动已表现出来，频谱中包含半频和基频两种频率成分，但随着时间增加，半频涡动幅值在切向油膜力作用下慢慢减小，最后稳态时只有基频涡动。

图7 转子动载荷e=50μmFig.7 Dynamic load e=50μm

图8 转子动载荷e=150μmFig.8 Dynamic load e=150μm

图9 不同动载荷下瞬态油膜力频谱图Fig.9 Spectrum diagram of oil film force under different dynamic load

图10 e=150μm的振动频谱图Fig.10 Spectrum diagram of the displacement e=150 μm

为了从瞬态流场的角度进一步分析半频涡动形成机理及随动载荷的变化情况，对应于图6～图8中的点，图11给出了相应的滑动轴承瞬态压力云图。由图11可知，当动载荷较小时(e=50 μm)，轴颈中心在B点时的承载区很明显的被右油槽和进油口分成两段，减弱了该处的油膜支撑刚度，表现为径向油膜力很小，甚至变为正值，而与B点基本对称的A点也受右油槽和进油口的影响，承载区变短，支撑刚度变弱，但由于距油槽距离较远，油膜压力区的变化没有B点那么明显，径向油膜力依然为负值，这就解释了半频涡动为什么出现在轴心轨迹的右边而非左边。

另外，随着动载荷的增大，轴颈和轴瓦的间隙变小，当轴心运动到C点时，上轴瓦很明显的形成了比较大的油膜压力，虽然这时油槽对承载区仍有破坏，但在上轴瓦比较大的油膜压力作用下，径向油膜力在C点位置处并未出现正值，保证了足够的支撑刚度，因此在相对较大的支撑刚度和阻尼的作用下，半频涡动被抑制了。

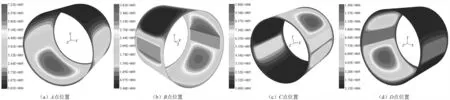
图11 动载荷作用下瞬态油膜压力分布云图Fig.11 Transient pressure distribution under dynamic load

4 多油楔滑动轴承

根据上节分析，径向油膜力和切向油膜力的增加能够起到抑制轴颈的不稳定运动。本节基于该结论从瞬态油膜力角度分析多油楔滑动轴承稳定性较好的原因，如图12～图14所示。油膜力分量值是随着动载荷的增加而增加，而且动载荷越大，油槽对油膜力分量的影响就越大，如当动载荷较小时(e=30 μm)，一个时间周期内三油楔轴承的油膜力分量只有两个波峰和两个波谷，但随着动载荷变大(e=100 μm)，由于三个油槽的影响，一个时间周期内三油楔轴承的油膜力分量出现了三个波峰和三个波谷。相对于圆柱形轴承在较小的动载荷作用下，出现正的径向油膜力，在多油楔滑动轴承中随着动载荷的增加径向油膜力和切向油膜力均不断增加，且始终保持负值，即可以提供足够的油膜刚度和阻尼保证转子稳定涡动，不出现半频。这是由于即使在小动载荷下油槽对于压力分布影响依然较小，且存在多个高压区，如图15所示。

图12 不同多油楔滑动轴承轴心轨迹随动载荷的变化过程Fig.12 Journal orbit of the multi-lobe journal bearings under different dynamic loads

图13 椭圆轴承油膜力分量随动载荷的变化过程Fig.13 Oil film forces of elliptical journal bearings under different dynamic loads

图14 三油楔轴承油膜力分量随动载荷的变化过程Fig.14 Oil film forces of three-lobe journal bearings under different dynamic loads

图15 e=30 μm椭圆轴承径向油膜力极大值点处压力云图Fig.15 Pressure distribution of elliptical journal bearings at extreme point e=30 μm

5 结 论

(1) 本文使用分流域结构化动网格技术实现了动载荷作用下圆柱形和多油楔滑动轴承的瞬态流固耦合计算，静平衡位置计算结果与试验结果的偏差小于2.5%，能够较为准确的分析轴颈涡动与非线性油膜力之间的耦合作用机制。

(2) 非线性油膜力支撑下，动载荷能够明显影响转子稳定性，较小的动载荷下油槽削弱了径向油膜力，导致轴颈涡动出现，但随着动载荷载荷的增加，油槽影响逐渐减弱，非线性油膜力的径向分量与和始终起阻尼作用的切向分量均不断增加，进而有效的抑制了轴颈半速涡动。

(3)相同工况下，多油楔滑动轴承压力分布受油槽影响较小，切向油膜力和径向油膜力始终保持负值，即能够提供足够的刚度和阻尼，进而增加了转子的稳定性。