考虑阻尼材料频变特性的结构响应计算方法

刘 岚， 刘雨侬,2， 刘 超， 刘 更， 吴立言， 岳彦炯

(1.西北工业大学 陕西省机电传动与控制工程实验室，西安 710072;2.中国运载火箭技术研究院，北京 100076；3.中国船舶重工集团公司第七〇三研究所， 哈尔滨 150078)

阻尼材料本身具有高耗能特性，可以在相当宽的频带范围内抑制结构的振动[1]。为了对附加阻尼结构减振性能进行越来越精确的评估，如何在考虑阻尼材料频变特性的情况下准确进行建模和振动响应计算成为附加阻尼结构振动响应分析的关键。

附加阻尼结构振动响应计算的基础在于对整体结构的准确建模。目前针对附加阻尼结构的建模方法可以分为复模量法、模态应变能及有限元法、解析法三大类[2]。复模量法应用在早期研究中，其忽略阻尼材料的频变特性，将弹性模量和损耗因子等效为常数处理。Ungar等[3]将阻尼材料的弹性模量近似为复常数，提出了阻尼结构的损耗因子及其计算方法，用来衡量结构的耗能属性。谭峰[4]在各个频段内选取常数弹性模量计入复模量法进行了建模，完成了箱体振动加速度和声辐射的计算，并通过试验验证了该方法基本满足工程应用。模态应变能及有限元法以有限元分析为主要手段，由Johnson等[5]在有限元法的基础上提出，通过各阶模态下的应变能分布求得各阶模态阻尼比。国内外学者对模态应变能法进行了深入的研究。Cura等[7]结合模态应变能法，提出了与频率相关的修正系数，间接考虑了材料频变特性。Hujare等[8]使用修正的模态应变能法在悬臂梁上进行布局设计并进行了试验验证。杨瑞[9]运用模态应变能法对简单结构进行了分析，并通过试验对结果进行验证。解析法主要包括分数导数模型和GHM(Golla-Hughes-Mctavish)模型。其中GHM法运用比较广泛，由Golla等[10]首先提出，后来经过Mctavish等[11]发展形成一套理论，可以在计入阻尼材料时考虑频变特性，但其只对简单梁、板结构进行了分析计算。Zghal等[12]用模态缩减法求解GHM模型中的微分方程，提高了该方法的计算效率。刘天雄等[13]基于哈密顿原理(Hamilton)，使用GHM模型与有限元法相结合，得到了结构的固有频率、模态阻尼比和响应。总而言之，复模量法主要假设阻尼材料的频变弹性模量为常数，在工程近似场合多使用这种简化计算方法。解析法主要在复合结构的动力学方程中引入阻尼材料的本构关系，理论上可直接考虑阻尼材料的频变特性，其理论清晰并能求得系统精确解，但由于方程的复杂性，它的求解依赖于简单结构和特殊边界条件，目前多用于简单二维结构模型中。模态应变能及有限元法主要通过有限元分析求得各阶模态的模态阻尼比，并可将其应用于基于模态的动力学响应计算中，但传统的模态应变能法没有考虑阻尼材料的频变特性。

对附加阻尼结构进行准确建模的最终目的是进行复合结构振动响应的精确计算。常用的结构振动响应计算方法包括完全法和模态叠加法。在完全法计算结构振动响应时，可以在时域求解过程中直接计入材料的阻尼系数，作为材料耗能属性加以考虑；而为了对复杂结构进行更加高效的计算，通常使用基于模态参数的模态叠加法进行结构振动响应计算[14]。阻尼系数作为其中一项重要的参数，对结构振动响应计算结果有较大的影响，目前取值基本依据工程经验、试验测量以及近似理论推导，存在有一定的局限性[15-17]。因此使用模态叠加法的前提是结构模态参数的准确提取，尤其是模态阻尼比的准确性。而目前附加阻尼结构在使用传统模态应变能法提取模态参数时无法准确计入阻尼材料的频变特性，在使用模态叠加法进行结构振动响应分析时也无法准确计入各阶模态的模态阻尼比。

针对上述两个问题，本文提出了一种考虑阻尼材料频变特性的结构响应计算方法。该方法建立了一种考虑阻尼材料频变特性的改进模态应变能法，准确提取了附加阻尼结构的模态参数；并在运用模态叠加法求解附加阻尼结构振动响应时将各阶模态参数准确计入，从而能够进行振动响应的准确计算。同时通过模态试验和振动响应试验验证了该响应计算方法的准确性。

1 理论基础

1.1 传统模态应变能法

模态应变能法是Johnson等在有限元法的基础上提出的，其基本思想是：在计算附加阻尼结构的模态应变能时，假设附加阻尼不会影响结构的模态振型，那么对于同一个结构可以用无阻尼模态近似代替有阻尼模态，通过无阻尼下的模态分析，得到各阶模态下阻尼层模态应变能和总模态应变能的分布情况，从而求得各阶模态的模态阻尼比。

在计算中，各阶模态的模态应变能如式(1)所示。

(1)

式中：V为附加阻尼结构的总体积；{φ}为附加阻尼结构的实模态向量。

附加阻尼结构的总体刚度矩阵[K]如式(2)所示。

(2)

因此结构总的模态应变能如式(3)所示。

(3)

式中：[K]M为非阻尼层金属材料的刚度矩阵；[K]V为阻尼材料的刚度矩阵。

通过这种方式将附加阻尼结构的总应变能分为非阻尼层应变能UM和阻尼层应变能UV。根据阻尼材料的耗能机理，可知阻尼层的耗能如式(4)所示。

(4)

式中：βV为阻尼材料的材料损耗因子。

通过模态损耗因子可以表征附加阻尼结构整体的耗能能力，其为阻尼层的耗能量与总模态应变能的比值。因此，附加阻尼结构某阶模态频率对应的模态损耗因子ηi如式(5)所示。

(5)

式中：i为附加阻尼结构的模态阶数。

由于在模态试验过程中直接得到的是模态阻尼比，所以在得到各阶模态损耗因子后，可由式(6)换算成各阶模态阻尼比ξi。

ηi=2ξi

(6)

由式(6)可知，传统模态应变能法用实特征向量替代复特征向量计算各阶模态阻尼比，可以大大地减小计算量。但是其在减小计算量的同时并没有考虑阻尼材料的频变特性，从而使得附加阻尼结构模态阻尼比计算的结果存在较大误差，因此必须建立一种可以考虑阻尼材料频变特性的建模方法。

1.2 模态叠加法求解振动响应

基于模态参数的响应计算一般使用模态叠加法，其基本原理是将多自由度的系统动力学问题解耦到模态坐标下，转化为一系列单自由度的动力学问题。多自由度系统动力学方程如式(7)所示[18]。

(7)

式中：M,C,K分别为系统的质量、阻尼和刚度矩阵；{u}为系统位移列向量；{Fa}为系统所受激励，一般为时间或频率的函数。

根据各阶模态特征向量的正交性，将上述物理坐标下的动力学方程解耦到模态坐标下，可得如式(8)所示的n个动力学方程。

(8)

式中：Mr为模态质量，Mr={φr}TM{φr}；Kr为模态刚度，Kr={φr}TK{φr}；Cr为模态阻尼，Cr={φr}TC{φr}=2Mrωrζr；Fr为模态力，Fr={φr}T{Fa}；其中r=1,2,…，h。

求解模态坐标下的动力学方程式(8)后可以得到每一阶模态所对应的模态参与因子ηr，将其代入式(9)即可求得系统的振动位移响应{u}，从而求出系统的振动速度和振动加速度。

{u}=η1{φ1}+η2{φ2}+…+ηn{φn}=Φ{η}

(9)

式中：Φ为模态矩阵，Φ=[φ1,φ2,…，φn]；{η}为模态参与因子列向量。

由式(8)可知，在系统振动响应计算中，对于一个确定的结构和确定的激励条件，模态质量Mr、模态刚度Kr和模态力Fr都是已知并确定的，只有模态阻尼Cr计入不够明确，而其决定参数是模态阻尼比ξr。

因此如果可以准确得到结构所有模态的模态阻尼比，那么就可以得到更加准确的结构振动响应。但是对于复杂的多自由度系统，求解全部模态的模态阻尼比基本上是不太可能的；另一方面是对于确定的激励工况，并不是结构的所有模态都可以被激起，大部分模态对振动的影响很小。因此在使用模态叠加法进行振动响应计算时并不需要计入结构的全部模态参数，只要将对振动响应贡献较大的有限n阶模态的模态阻尼比ξr进行准确计入，即可得到更准确的振动响应计算结果。

2 考虑阻尼材料频变特性的结构响应计算方法

为了对附加阻尼结构的振动响应进行准确计算，提出了考虑阻尼材料频变特性的结构响应计算方法。该方法在传统模态应变能法的基础上，建立了一种考虑阻尼材料弹性模量和损耗因子频变特性的改进模态应变能法，通过迭代准确提取附加阻尼结构的模态参数；并在运用模态叠加法求解复合结构振动响应时将各阶模态的模态参数准确计入，从而得到附加阻尼结构振动响应的准确计算结果。在仿真的同时通过模态试验验证了模态参数提取的准确性，并通过振动响应试验验证了该方法求解振动响应的准确性。详细流程如图1所示。

图1 考虑阻尼材料频变特性的结构响应计算方法Fig.1 Calculation method of structural response considering dynamic characteristics of damping materials

3 改进的模态应变能法

3.1 阻尼材料的频变特性

阻尼材料属性具有随激励和温度变化的特性[19]。在稳定的外界温度下，不同型号阻尼材料的属性随激励频率的变化特性不同。为了准确考虑阻尼材料的频变特性，本文根据厂商提供的SA-3C型阻尼材料的属性表，通过最小二乘法拟合得到该材料的弹性模量与损耗因子随频率变化的规律，如图2所示。其中E(f)为阻尼材料频变弹性模量;β(f)为阻尼的频变材料损耗因子；f为频率。

图2表明阻尼材料的弹性模量和材料损耗因子受激励频率的影响明显，在不同的模态频率下对应的材料属性是不相同的。因此在求解各阶模态阻尼比的过程中，根据阻尼材料频变特性曲线对模态应变能法中的阻尼材料属性进行修正，可以得到准确的模态参数。

图2 SA-3C型阻尼材料频变特性Fig.2 Dynamic characteristics of SA-3C

3.2 考虑阻尼材料频变特性的改进模态应变能法

本文提出了一种考虑阻尼材料频变特性的改进模态应变能法。即在传统模态应变能法基础上，引入SA-3C材料的弹性模量和材料损耗因子随激励频率的变化规律，通过迭代修正各阶模态频率对应的材料参数，完成附加阻尼结构的建模及模态参数的准确计算。

如图3所示为使用本文改进模态应变能法求解M阶模态参数的计算流程，具体计算步骤如下：

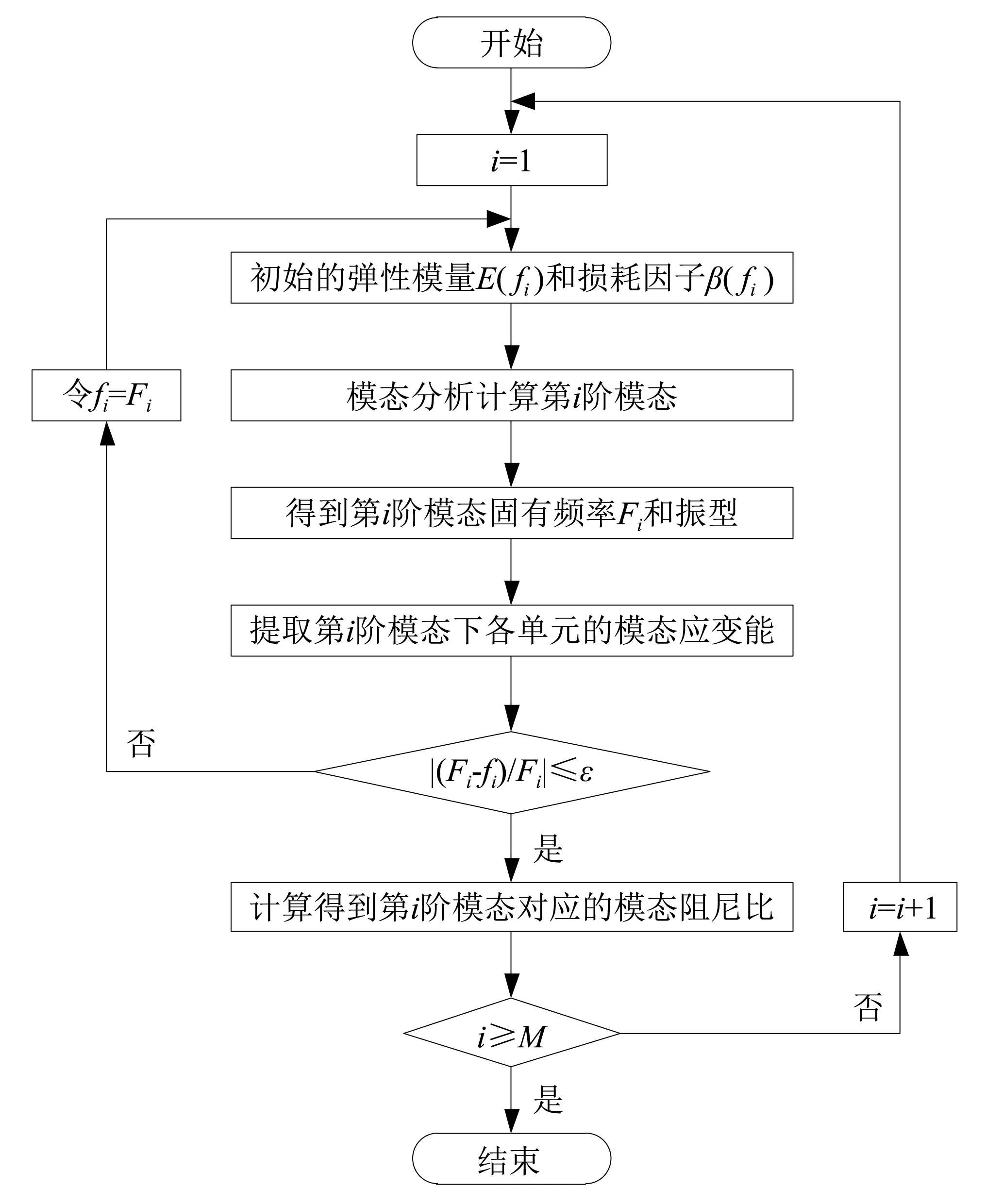
图3 改进模态应变能法计算流程图Fig.3 Flow chart of improved modal strain energy method

步骤1确定阻尼材料的类型、激振力的频率范围；

步骤2选取激振频率范围的均值fi对应的弹性模量E(Fi)和损耗因子β(Fi)，将其作为初始材料参数计入模态应变能法中对结构进行模态分析，得到第i阶固有频率Fi与对应振型；

步骤3将第i阶固有频率Fi和最初计入的材料属性对应的频率值fi通过|(Fi-fi)/Fi|≤ε进行判定。若满足判定条件，输出第i阶模态的模态应变能分布；若不满足判定条件则返回步骤2中修正阻尼材料参数为E(Fi)，β(Fi)，再次进行模态分析，直到满足判定条件后停止迭代计算；

步骤4通过第i阶模态应变能分布，利用模态应变能法求出模态损耗因子，进而求出该阶模态阻尼比；

步骤5重复以上步骤2～步骤4完成其它阶模态对应模态阻尼比的计算；

步骤6输出M阶模态的固有频率、振型和模态阻尼比。

3.3 仿真与试验模型

为了验证改进模态应变能方法的准确性，本文以约束阻尼结构的矩形板为研究对象，将仿真与试验结果进行对比验证。

矩形板的几何尺寸如图4所示。其中，基层材料为钢，弹性模量E1=201 GPa，密度为ρ1=7 850 kg/m3，泊松比为μ1=0.3，长宽厚为400 mm×400 mm×2 mm；阻尼层选用SA-3C型阻尼材料，其频变弹性模量E(f)与损耗因子β(f)如图2所示。密度为ρ2=1 450 kg/m3，泊松比为μ2=0.495，长宽厚为300 mm×300 mm×2 mm；约束层的材料为铝，弹性模量为E3=68.9 GPa，泊松比为μ3=0.3，长宽厚分别为300 mm×300 mm×1 mm，密度为ρ3=2 700 kg/m3。约束阻尼结构的边界条件为基层四边的固支约束，阻尼层和约束层覆盖在基层的正中部，三者共同构成约束阻尼板结构。

图4 算例模型图(mm)Fig.4 Example model(mm)

3.4 模态参数提取及试验验证

首先进行模态参数的仿真提取。依据SA-3C阻尼材料的频变特性，使用改进模态应变能法进行迭代计算，提取了考虑阻尼材料频变特性的各阶模态参数，包括固有频率、模态阻尼比和振型。使用改进模态应变能法仿真计算得到的结果见表1。

本文通过约束阻尼板的模态试验对改进模态应变能法提取模态参数的准确性进行验证。试验模型与仿真模型一致，将复合矩形板的基层四边固定在刚性架上达到四边固支的效果。由于基层板正面粘贴了约束层和阻尼层，为测试基层结构在附加阻尼材料后的振动响应，在基层板反面布置9×9=81个测点，试验模型基层测点布置和实测图，如图5所示。模态试验使用的激励方式是移动力锤法，选用DYTRAN 5800B4型冲击力锤，通过预试验得到力谱曲线可知有效试验频率范围为0～750 Hz，故本文只研究该范围内的模态特性。模态试验后进行了数据的处理，主要包括频响函

数拟合、模态参数提取。通过数据处理，可以得到模态叠加法所需要的模态参数，包括固有频率、主振型和模态阻尼比，模态试验结果如表1所示。

图5 基层测点布置与实测图Fig.5 Test points distribution diagram

表1 仿真与试验模态参数对比

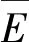
最后将模态试验和改进模态应变能法仿真得到的前五阶振型图进行对比，结果如图6所示，仿真和试验得到的各阶模态振型一致，表明了在试验和仿真中不存在丢失模态的情况。

根据表1和图6的结果，将改进模态应变能法、传统模态应变能法提取的模态参数与模态试验结果进行对比。改进模态应变能法提取固有频率的误差范围为-3.04%～3.41%，模态阻尼比的误差范围为-0.03%～3.71%，其提取的模态参数与模态试验结果较为接近。而传统模态应变能法提取固有频率的误差范围为0.84%～21.19%，模态阻尼比的误差范围为-10.84%～-17.02%，其仅在第四阶与模态试验结果较为接近，其余各阶均存在较大误差。

出现上述结果的原因是传统模态应变能法计入的材料参数为平均频率375 Hz对应的阻尼材料属性，所以该方法的分析结果在375 Hz附近可以得到比较准确的模态参数，但是在远离该频率的情况下，其结果与试验数据相比存在误差。而本文的改进模态应变能法在计算过程中通过迭代，不断修正材料的频变弹性模量和损耗因子，因此各阶模态的固有频率和模态阻尼比结果与模态试验结果更接近。

图6 试验与仿真振型图对比Fig.6 Comparition of experiment and simulation modes

4 基于模态参数的振动响应分析与试验

在改进模态应变能法准确提取模态参数的基础上，本文使用模态叠加法进行了基于模态参数的结构振动响应分析，并与振动响应试验结果进行对比。

分析模型仍使用上文所述的约束阻尼结构模型。在基层上选取相应的激振点和测试点进行振动响应分析，激振点与测试点位置如图7所示。根据本文建立的考虑阻尼材料频变特性的结构响应计算方法，为取代原有模态阻尼比的经验值，将上文提取到的各阶模态参数准确计入模态叠加法中进行振动响应计算，分别计算激振点1和点2时测试点的振动响应。同时在相同约束状态下使用激振器进行振动响应试验，将试验结果与仿真计算结果进行对比。图8为试验与仿真的加速度频响结果对比，其中图8(a)和图8(b)分别显示当激振点1或激振点2被激励时，仿真和试验中测试点的振动加速度频响曲线。

图7 激振点与测试点位置分布图Fig.7 The distribution of excitation points and test point

图8 试验与仿真的加速度频响结果对比Fig.8 Comparison of acceleration frequency response results between experiment and simulation

对比仿真和试验数据可知，基于本文方法进行的结构振动响应仿真结果基本和试验结果吻合。在频率0～500 Hz内，仿真和试验结果的共振频率误差不大于5%，共振峰值的误差不大于12%，二者基本吻合；而在频率500～750 Hz内，仿真和试验结果的共振频率误差不大于5%，共振峰值的误差不大于25%；超过750 Hz后共振频率和共振峰值的误差变大，这是由于试验过程中，附加阻尼材料后约束阻尼结构整体刚度下降，激励锤与试件接触时间增加，会导致激振力的有效频率范围降低，因此超过该频率范围的试验数据会产生较大的误差，导致仿真与试验数据差异变大。但总体来看，上述振动响应数据的对比分析可以验证本文方法在0～750 Hz频段内计算附加阻尼结构振动响应问题上的准确性和有效性。

5 结 论

本文在传统模态应变能法和模态叠加法的基础上，建立了一种考虑阻尼材料弹性模量和损耗因子频变特性的结构响应计算方法。并通过模态试验和振动响应试验对使用该方法的模态分析与振动响应仿真结果进行了对比验证。得到主要结论如下：

(1)根据厂商提供的SA-3C型阻尼材料的材料属性，拟合得到了该材料的弹性模量与损耗因子随频率变化的规律。得出了阻尼材料属性受激励频率影响较为明显的结论，明确了阻尼材料频变特性对附加阻尼结构振动响应计算的准确性有较大影响。

(2)本文提出的改进模态应变能法以有限元法为基础，用实特征向量替代复特征向量计算各阶模态阻尼比，能够在复杂结构的模态参数提取过程中减小计算量；其次通过迭代计入了阻尼材料的频变特性，保证了模态参数的准确提取。本文方法相比解析法能更快速地提取三维复杂结构的模态参数，相比复模量法和传统模态应变能法的准确性更高。同时本文方法提取模态参数的准确性得到了模态试验的验证，仿真值和试验值的误差小于3.71%。

(3)本文提出的考虑阻尼材料弹性模量和损耗因子频变特性的结构响应计算方法，在通过改进模态应变能法提取准确的模态参数基础上，基于模态叠加法进行振动响应计算时用准确的模态阻尼比替换原有的经验值，进行了准确的振动响应计算，并与振动响应试验结果进行对比，验证了该方法的准确性。

(4)本文以约束阻尼板结构为模型进行仿真和试验，对于仿真频段和试验频段的准确性有较大的限制。在0～750 Hz的频段范围内，本文提出的考虑阻尼材料弹性模量和损耗因子频变特性的结构响应计算方法得到的分析结果更加接近实际的试验结果；在750 Hz以上频段出现较大误差，原因是在预实验中力锤的力谱曲线显示有效试验频率范围为0～750 Hz。因此为了进一步验证本文方法在复杂结构和更宽频段范围上的准确性，针对三维复杂结构的验证性试验将是后续研究的方向。