基于裂缝分布特征的RC框架中间节点受剪性能计算拉压杆模型
董俊宏, 杨 红,2, 赵雯桐
(1.重庆大学 土木工程学院,重庆 400045;2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆 400045)
大量震害结果表明,钢筋混凝土框架结构中若节点先于梁端、柱端出现塑性铰而发生剪切破坏,则一般会造成严重损失。因此,对节点区进行正确的计算分析、抗震构造设计是确保结构抗震性能的重要环节。采用有限元方法模拟节点的受力规律时,正确计算节点区的剪应力-剪应变关系曲线是有限元模型合理、非线性变形计算结果准确的基础和前提。因此,正确计算节点的剪应力-剪应变关系是亟待解决的问题。
在计算节点受力性能时,拉压杆模型因传力机理清晰、适用于D区(平截面假定不符合区域)等优势,受到了众多学者的青睐。20世纪90年代,Schlaich[1]提出了拉压杆模型设计方法,为拉压杆模型在D区的应用奠定了基石。Hong等[2]提出了基于变形的拉压杆模型,该模型的次斜压杆布置方式合理,符合节点桁架机构的力学性能。Mitra等[3-4]提出了一种分布式桁架拉压杆模型,该模型的主要特点是水平拉杆和竖向拉杆的交点均设置铰接点。Hwang等[5]建议了一种软化拉压杆模型,该模型由主斜压杆机构、水平机构和竖向机构组成,其建立原则基本符合节点的传力机理。Park等[6]针对钢筋混凝土柱提出了一种拉压杆模型的建立方法,其拉杆、压杆和结点的模型化思路有一定的创新性。此外, Paulay等[7-8]、Kitayama等[9]和Lowes等[10]等均对混凝土节点的抗震性能进行了大量研究工作,促进了拉压杆模型的发展。
综上所述,节点拉压杆模型的主要特点和原则是,计算模型的构成应反映主斜压杆机构、桁架机构和约束机构的特点;次斜压杆的布置形式多样,大致平行于节点主对角线;结点通常视为理想铰接点以达到简化计算的目的;水平拉杆代表箍筋。
前述已有节点拉压杆模型多是为计算节点的抗剪承载能力而提出的,其建立过程一般未考虑计算节点的剪应力-剪应变骨架线的相关问题。为此,本文基于梁柱组合体抗震性能试验中节点裂缝的发展规律和分布特征,提出了一种新的节点拉压杆模型并应用于剪应力-剪应变骨架线的计算。最后,利用OpenSees有限元软件中的超级节点单元模拟梁柱组合体抗震性能试验,对本文提出的拉压杆模型的有效性和适用性进行了验证。
1 基于裂缝分布的拉压杆模型
1.1 模型介绍及基本假定
图1为4个梁柱组合体抗震试验结果[11],其裂缝分布规律较为一致。本文基于节点区混凝土的裂缝发展规律及试验结束后裂缝的分布特征,在考虑了前文所述,各典型拉压杆模型的优点后提出了基于裂缝分布的拉压杆模型,如图2所示。从图2可知,斜压杆AE代表主斜压杆机构,水平拉杆、竖向拉杆及次斜压杆代表桁架机构,约束机构则通过采用Mander约束混凝土本构关系[12]体现。

图1 节点裂缝分布Fig.1 The crack distribution of joint
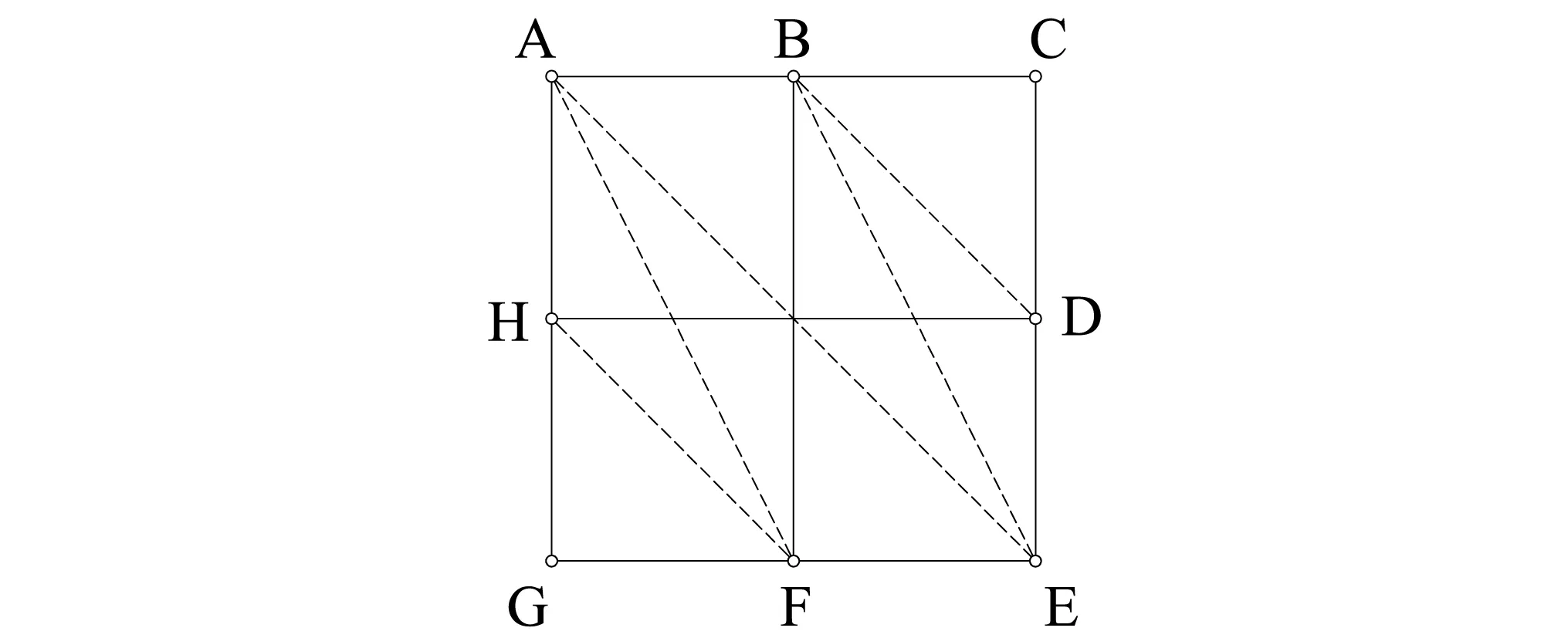
图2 基于裂缝分布的拉压杆模型Fig.2 The crack-based strut-and-tie model
为了简化计算,并提高该模型的通用性,对该模型采用了以下6个基本假定:
①计算中不考虑节点保护层混凝土。
② 拉杆变形假定。
本文假定只有水平中拉杆HD能产生轴向变形,忽略竖向边拉杆AG和CE、竖向中拉杆BF和水平边拉杆AC和GE产生的轴向变形。提出这一假定的主要原因是基于柱纵向钢筋一般远大于节点水平箍筋的事实。此外,根据傅剑平等[13-15]的试验结果可知,节点中间层水平箍筋应变最大,靠近节点上、下边缘的箍筋应变较小(一般明显低于屈服应变),节点两侧柱纵筋的应变明显低于屈服应变,节点正、背面柱纵筋应变最小。这些试验结果均表明假定②是合理的。
③ 假定结点均为理想铰接点。
一方面,节点区域属于D区,为了体现节点不符合平截面假定的事实,此模型竖向边拉杆和水平边拉杆中的结点均采用完全铰接的形式;另一方面,假定结点均为理想铰接点并完全铰接有助于简化计算。不少学者也采用了这一做法[16]。
④ 假定各压杆截面高度之和等于节点核心区。对角线长度在垂直于另一条对角线的平面上的投影长度,具体计算方法见“1.2”节。
⑤ 为简化计算过程,假定次斜压杆AF的截面面积等于次斜压杆BE的截面面积,次斜压杆HF的截面面积等于次斜压杆BD的截面面积。
⑥ 忽略箍筋和混凝土的黏结,近似认为箍筋处于理想受拉状态,沿长度方向应力、应变均匀分布。
1.2 压 杆
1.2.1 主斜压杆
为简化计算,将主斜压杆AE定义为等直杆。主斜压杆的截面面积是对节点抗剪性能有重要影响的主要参数,可按以下方法计算。
1)主斜压杆横截面高度hstrut
主斜压杆截面高度hstrut按照式(1)和式(2)进行计算。
(1)
(2)
式中:cb为梁压区高度;cc为柱压区高度,分别如图3所示。由于梁柱组合体试件的梁端一般首先屈服并进入非线性受力,故梁可采用达到承载力极限状态时的受压区高度,Hwang等建议cb取为hb/5。hb,hc分别为梁、柱截面高度,N为柱轴力,Ag为柱截面面积,fc为节点的混凝土轴心抗压强度。
由于轴压比和节点形状尺寸的差异,按此方法计算得到的面积是主斜压杆的斜截面面积,并不是垂直于对角线的截面面积,如图3所示。
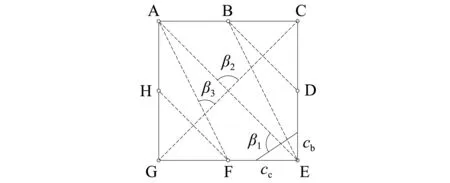
图3 压杆正截面夹角Fig.3 Angle of cross-section of strut
因此,斜压杆截面高度应按式(3)进行修正
hstrut=h·sinβ1
(3)
式中:h为按式(1)和式(2)计算所得结果;β1为h所在直线与对应的节点核心区主对角线的夹角(见图3)。
2)主斜压杆横截面宽度wsturt
主斜压杆横截面宽度wstrut可按式(4)计算
wstrut=b-2×(c+djh)
(4)
式中:b为节点宽度;c为节点保护层混凝土厚度;djh为节点水平箍筋的直径。
根据美国ACI规范[17]的建议,结合Mander约束混凝土的本构关系计算主斜压杆混凝土抗压强度。因此,主压杆的轴力Fn按式(5)计算
Fn=0.85·βs·σc·A
(5)
式中:σc为压杆应力;A为压杆横截面面积。参考美国ACI规范的建议,压杆的力折减系数βs取0.75。
1.2.2 次斜压杆
在软化拉压杆模型中,水平机构中的次斜压杆与竖向机构中的次斜压杆相交,这违背了压杆不相交的基本原则。因此,这两种次斜压杆必须舍去其一。基于图1的裂缝分布规律,结合软化拉压杆模型和分布式桁架拉压杆模型中次斜压杆的布置方式,本文建议次斜压杆AF,BE,BD和HF按图2的方式布置。
次斜压杆的截面宽度计算方法与主斜压杆相同。次斜压杆截面高度则参考王田友等[18]的计算方法。本文建议按以下步骤进行计算:
步骤1 计算节点核心区对角线长度lstrut
步骤2 根据假定④,求次斜压杆总高度hz
hz=lstrut·sinβ2
(6)
式中:β2为对角线夹角(见图3)。
步骤3 计算待分配高度hd
hd=hz-hstrut
(7)
步骤4 暂取次斜压杆BE与次斜压杆BD的面积比为5∶4,根据假定④和假定⑤可得
(8a)
(8b)
式中:hBE,hAF,hBD和hHF分别为次斜压杆BE、次斜压杆AF、次斜压杆BD和次斜压杆HF的截面高度;β3为次斜压杆AF与对角线的夹角(见图3)。次斜压杆的轴力仍按式(5)计算。
1.3 拉 杆
三根水平拉杆HD,AC和GE由节点区水平箍筋组成,共同体现桁架机构的贡献。在外荷载作用过程中,各节点箍筋受力不均,一般仅部分箍筋达到屈服,且节点中部箍筋的应变皆大于节点上、下边缘处的箍筋应变。因此,可借鉴Hwang等提出的节点箍筋有效层数的概念(见表1)进行分析。

表1 箍筋有效层数
基于箍筋有效层数的概念,邢国华等[19]认为仅65%的节点区箍筋受力充分。故本文建议按下述公式计算水平中拉杆的横截面面积AHD
AHD=0.65·n·m·Ajh 1
(9)
(10)
式中:Ajh为节点水平箍筋面积之和;n为箍筋平行于梁纵筋方向的肢数;m为节点区箍筋层数;Ajh 1为节点区单肢箍筋的面积。
水平中拉杆的轴力可根据结点H的平衡条件求得。此外根据美国ACI规范,水平中拉杆的轴力THD与水平中拉杆的应力σHD存在下述关系
THD=βn·σHD·AHD
(11)
根据美国ACI规范, H,D结点属于C-C-T类型节点,因此拉杆力折减系数βn=0.8。
根据假定②,仅水平中拉杆须考虑钢筋变形。本文采用常用的双折线钢筋本构关系进行计算。
2 模型变形协调条件和受力平衡条件
2.1 变形协调条件
本文以θFED为基本变量建立考虑变形协调的迭代判别式。
图4是节点发生剪切变形时基于裂缝分布的拉压杆模型建立的变形图。根据假定②和变形协调原则,竖向中拉杆BF因转动产生的水平位移应等于水平边拉杆AC产生的水平位移,主斜压杆的轴向压缩变形按式(12)计算
dlAE≈-θsz·lBF·cosθBAE
(12)
在变形过程中,由几何关系可知
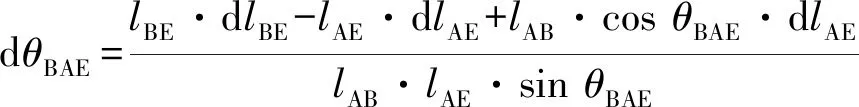
(13)
(14)
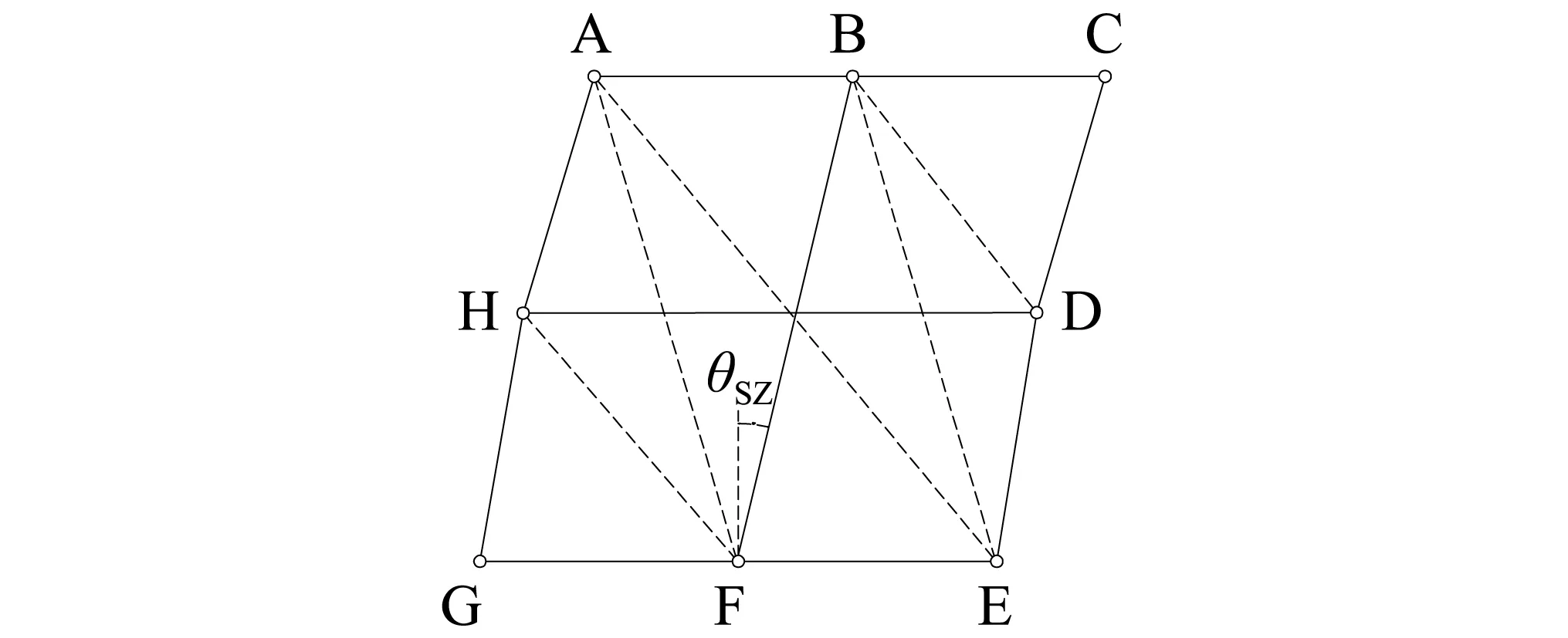
图4 基于裂缝分布的拉压杆模型剪切变形示意图Fig.4 Shear deformation of crack-based strut-and-tie model

(15)
则因压杆变形而形成的θFED为
θFED=θBAE+θEAF+θBED+dθBAE+dθEAF+dθBED
(16)
除上述方法外,θFED也可由下述方法求得。变形后的θFED与dθHGF、拉杆HD的变形dlHD有如下关系
(17)
为满足变形协调条件,由式(16)的计算结果与式(17)的计算结果应相等,故可建立以下变形协调条件判断式
(18)
2.2 力平衡条件
此模型的力平衡状态由A,C,E,G,B,D,F,H等共8个结点的平衡条件决定。
2.2.1 角部结点
对于A,C,E和G 4个角结点,由于外力可以随作用在结点上内力而变化,因此,结点A,C,E和G的力平衡关系可自动满足。
2.2.2 中部结点
假定次斜压杆HF的应变后,利用力平衡条件,以结点H,D和B为分析对象,可按常规力学方法求解竖向中拉杆和水平中拉杆的内力。最后,以结点F作为校核结点,若在结点F满足平衡条件的情况下,各压杆同时也满足变形协调条件,则该模型符合迭代计算要求。
在受力过程中,因次斜压杆HF和BD的轴力、AF和BE的轴力分别始终相等,故结点F自动满足力平衡条件。因此,只要变形协调条件满足,基于裂缝分布的拉压杆模型可自动满足力平衡条件。
3 节点剪应力和剪应变计算公式
1) 节点剪应力
节点水平剪力等于各压杆轴力的水平分量之和,节点水平剪应力τ可按式(19)计算
(19)
式中:Fni为第i个压杆的轴力;αi为第i个压杆与水平线的夹角;bj为节点侧面有效宽度;bc为节点正面有效宽度。
2) 节点剪切变形
如图4所示,本文将竖向中拉杆的转角θsz作为节点平均剪切角γ,即有
γ=θsz
(20)
4 程序流程图
根据上述压杆、拉杆的应力、应变及轴力、变形计算公式,结合变形协调条件及力平衡条件等,在Matlab平台上编制了基于裂缝分布的拉压杆模型剪应力-剪应变骨架曲线的计算程序,程序流程见图5。
5 试验验证
选取17个梁柱组合体试件的试验结果[20-21]对基于裂缝分布的拉压杆模型所计算的节点剪应力(τ)-剪应变(γ)曲线的合理性进行了验证。图6的对比结果表明,本文建立的模型能较为有效地计算节点的τ-γ骨架曲线,计算曲线与试验结果整体吻合较好。此外,将τ-γ曲线的峰值应力计算结果、相应试验结果以及误差百分比汇总于表2,其平均误差为10.85%,计算精度在合理范围内。

图5 程序流程图Fig.5 Program flow chart

表2 峰值应力的模拟结果与实验结果

图6 各试件剪应力-剪应变骨架曲线Fig.6 The shear stress-strain skeleton curves of specimens
为进一步说明本文建立的基于裂缝分布的拉压杆模型的合理性,下面将验证各压杆的受力情况。
节点斜裂缝发展的一般规律是,沿节点核心区对角线方向首先出现主裂缝,然后在这条主裂缝两侧,以平行于对角线方向逐步出现新的斜裂缝,且对角线附近的裂缝发育最为明显,裂缝宽度最大。可见,这些位置的主拉应力最大,其他位置拉应力相应减小。该现象说明本模型的主斜压杆的压应力最大,远离对角线的的次斜压杆的压应力更小。
因此,如果基于裂缝分布的拉压杆模型中各压杆的压应力符合主斜压杆最大、两侧次斜压杆依次递减的规律,则该模型的受力机理比较合理。
限于篇幅,仅以试件J-2和J-5为例进行说明,模型各压杆的压应力计算结果如图7所示。图7表明,主斜压杆受力最大、次斜压杆BE受力次之、次斜压杆BD受力最小,符合前述受力规律。
6 基于超级节点单元的节点剪切模型应用
将本文提出的基于裂缝分布的拉压杆模型用于多个典型梁柱组合体试验的有限元模拟分析之中,可验证该模型的有效性、适用性。
Lowes等[22]提出了一种基于转动铰模型的二维超级节点单元模型。其结构较为严谨、体系较为完整,能够较为有效地描述节点区各分量之间的关系,具有可操作性强、计算效率高、收敛性好等特点。
各梁柱组合体试验均采用OpenSees平台的梁柱节点单元(超级节点模型)模拟节点区的非线性受力性能。超级节点模型中,节点剪切块的τ-γ骨架曲线采用本文提出的基于裂缝分布的拉压杆模型计算确定。

图7 压杆应力-节点剪应变关系曲线Fig.7 The compression stress-shear strain curves of struts
6.1 超级节点模型节点剪切块的定参方法
节点剪切块的τ-γ骨架线定参方法如下:
1)第一个关键点P1是图8中直线上升段的顶点,为简化计算,剪应力τp1近似取τp2的一半;γp1则根据节点τ-γ曲线的计算结果取与P1点对应的剪应变。
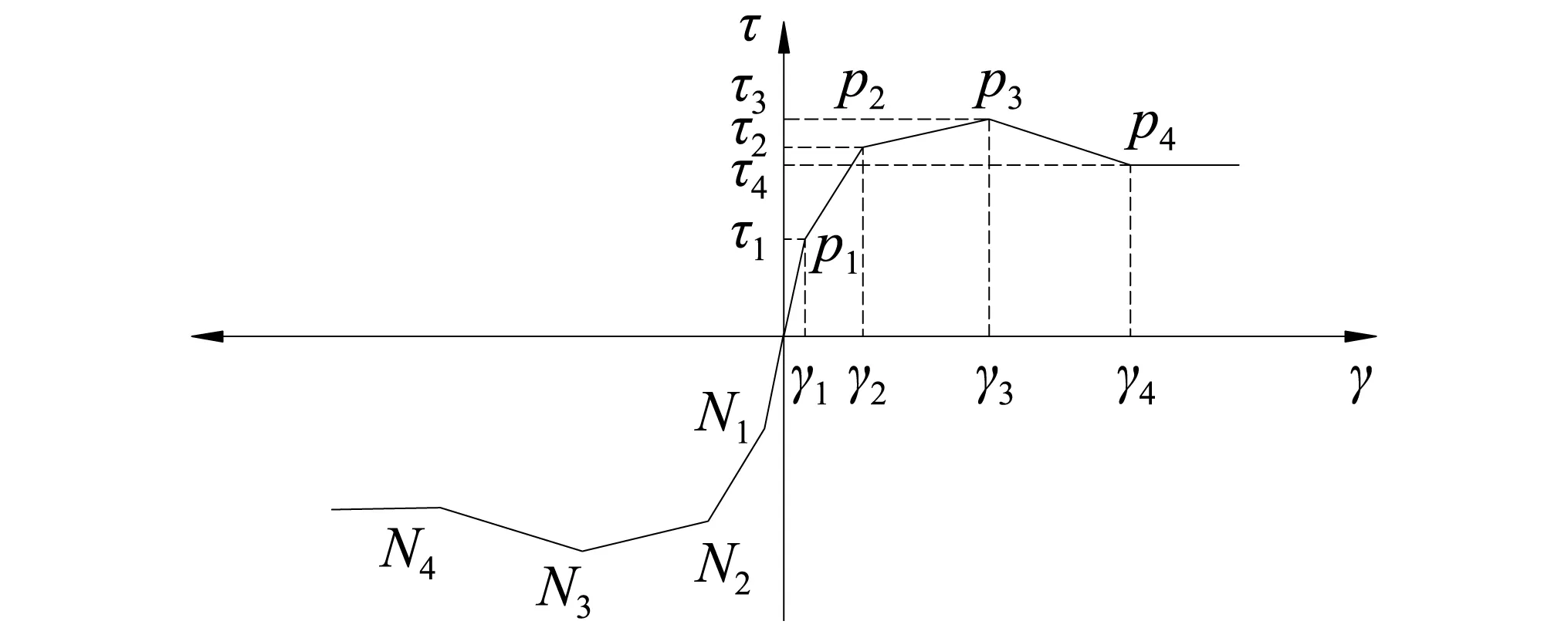
图8 节点剪切块剪应力-剪应变骨架曲线关键点Fig.8 Key points of shear stress-strainskeleton curve of joint shear block
2)P2节点τ-γ曲线上刚度第一次明显变小的关键点(类似于“屈服点”),τp2取计算所得τ-γ曲线的第一明显转折点对应的剪应力,γp2取相应的剪应变。
3)P3为峰值点,τp3取峰值应力,γp3取对应的剪应变。
4)P4为极限点,τp4取应力下降到峰值应力的80%时所对应的剪应力值,γp4取对应的剪应变。
6.2 典型算例
选取梁柱组合体试件J-6,J-7,J-8和J-10作为典型算例,并利用OpenSees程序完成相应的梁柱组合体试验的有限元模拟。
6.2.1 有限元模型的建立
如图9所示,采用OpenSees程序对该梁柱组合体抗震性能试验进行模拟计算时,应分别确定分析对象中各节点的位置、节点集中质量、材料本构关系、截面恢复力模型、单元类型、外加荷载种类、几何坐标转换类型和约束形式等,常规参数的取值可参考OpenSees用户手册[23]。

图9 梁柱组合体有限元模型Fig.9 Beam-column finite element model
(1)单元类型
1)梁柱单元
采用非线性梁柱单元模拟梁、柱构件,各积分点的截面恢复力模型采用纤维模型,梁取3个积分点,柱取4个积分点(见图9)。
2)节点单元
节点采用超级节点单元进行模拟。其中,节点剪切块的定参方法详见“6.1”节,界面剪切分量采用弹性材料模拟,纵筋黏结滑移特征则采用Lowes等建议的模型进行模拟。
超级节点单元的纵筋黏结滑移分量采用一维捏缩材料模型模拟。Lowes等通过锚固钢筋的拉拔试验数据,并对节点核心区黏结应力分布进行简化的基础上,建立了用于近似模拟贯穿节点核心区纵筋黏结滑移的有限元模型。
(2)截面对象
选择Fiber Section梁柱单元截面恢复力模型,具体详见OpenSees用户手册。
(3)混凝土和钢筋本构关系
采用基于Kent-Scott-Park模型的单轴混凝土应力-应变模型Concrete01 Material定义梁、柱的混凝土纤维,钢筋纤维采用Steel02 Material单轴材料本构模型定义。
6.2.2 梁柱组合体试件的模拟结果分析
依据上述超级节点剪切块的定参方法,由基于裂缝分布的拉压杆模型进行计算,可得到试件J-6、试件J-7、试件J-8和试件试件J-16的节点τ-γ骨架线的4个关键点,分别如表3所示。
然后,采用OpenSees进行有限元模拟,可得到各试件的节点剪切块的τ-γ滞回曲线,以及梁端力-位移滞回曲线的模拟结果,分别如图10、图11所示。
对比结果表明,本文提出的基于裂缝分布的拉压杆模型对梁柱组合体抗震性能试验的模拟效果较好。

表3 节点剪应力-剪应变骨架线的各关键点计算结果

图10 剪切块剪应力-剪应变滞回曲线Fig .10 The stress-strain hysteretic curve of shear panel

图11 梁端力-位移滞回曲线Fig.11 The load displacement loops of specimen
7 结 论
为解决钢筋混凝土框架结构中间层中节点的剪应力-剪应变骨架线计算问题,提出了基于裂缝分布特征的拉压杆模型,并得到以下主要结论。
(1)根据钢筋混凝土框架中间层中节点的受力机理,提出了建立拉压杆模型的基本原则和基本假定。
(2)提出了基于裂缝分布特征的拉压杆模型,推导了变形协调关系和力平衡方程,建立了节点区的剪应力-剪应变骨架线计算方法,编制了计算程序。
(3)根据17个梁柱组合体试件的试验结果对提出的拉压杆模型的合理性进行了验证,效果较好。
(4)采用多个典型梁柱组合体抗震试验的有限元模拟分析与试验结果的对比,进一步验证了基于裂缝分布的拉压杆模型在OpenSees中的梁柱节点单元中的适用性和有效性。

