渤海夏季第一斜压罗斯贝变形半径的计算与分析
张晓璐,熊学军*
(1.国家海洋局 第一海洋研究所,山东 青岛266061;2.海洋环境科学和数值模拟国家海洋局重点实验室,山东 青岛266061)
渤海,是一个深入中国大陆的半封闭浅海,北、西、南三面被陆地包围,仅通过东面的渤海海峡与黄海沟通。注入渤海的沿岸河流众多,北有辽河、大辽河、大凌河,西有海河、滦河,南有黄河、小清河,因此形成了渤海独特的水文特征及动力结构。相较于冬季,渤海夏季的风速小,主要为热盐流。近年来,大量的数值模拟工作及调查研究表明,夏季渤海多存在一些局地范围的环流,如渤海中部的顺时针环流,长兴岛以西的辽东湾海域的逆时针环流,以及在渤海南部的莱州湾存在弱的顺时针环流等[1]。
在海洋环流的理论研究和数值模拟中,罗斯贝变形半径是一个极其重要的水平尺度,它描述了地球旋转对流体运动的影响。这个概念,最早是由Carl-Gustav Rossby于1938年在研究地转调整中提出的。若海面高度变化在调整过程中的尺度与罗斯贝变形半径相比为小量,则压强梯度非常大,重力支配运动的状态;但是,当海面高度的变化发展到具有罗斯贝变形半径尺度的范围时,科氏力项变得同压强梯度项同等重要[2]。简言之,即在罗斯贝变形半径这个距离尺度上,科氏力使自由面变形的趋势与压强梯度力使自由面复原的趋势相平衡。在海洋中,斜压罗斯贝变形半径是一种常与边界现象(诸如边界流、锋面)以及涡旋有联系的自然尺度,是设置数值模式参数的重要参考。有研究表明,在模拟中尺度运动时,网格大小应当是罗斯贝变形半径的一半,或者是其三分之一[3]。
国外对斜压罗斯贝变形半径的研究已有不少。Emery等[4]在1984年用气候态的温盐剖面数据计算了北太平洋和北大西洋的斜压罗斯贝变形半径;Houry等[5]在1987年用NODC的温盐数据计算了南大西洋的斜压罗斯贝变形半径;特别地,Chelton等[6]在1996年利用NODC的1°×1°的气候态的温盐数据计算了全球大洋的第一斜压罗斯贝变形半径以及对应的全球范围的第一斜压重力波相速度,对后来学者的研究工作起了重要的启示和参考作用。除了大洋中,在内海也有针对斜压罗斯贝变形半径的专门研究,如Fennel等[7]、Alenius等[8]以及Osinsik等[9]曾分别利用航测温盐剖面数据计算了波罗的海、芬兰湾的斜压罗斯贝变形半径。但在国内,有关斜压罗斯贝变形半径的研究工作不多,甘子钧和蔡树群[9],蔡树群等[10],曾用Levitus和NODC标准层上的气候态的温盐资料计算过南海斜压罗斯贝变形半径的地理及季节变化以及相应的第一斜压重力波相速度。
在渤海进行第一斜压罗斯贝变形半径的计算和研究尚未发现。本文在观测数据基础上,分别利用WKB近似和数值解法,对渤海夏季第一斜压罗斯贝变形半径进行了计算和分析,希望有助于渤海环流、中尺度涡旋,以及与此相关的其他海洋现象的研究。
1 资料
本文所用资料为渤海2006年夏季的温度和盐度大面观测资料,观测仪器为日本ALEC公司的AAQ1183系列的CTD,观测时间为2006-07-18—08-12。为方便对下文计算结果分析对比,将整个渤海划分为6个区域,分别为渤海东部海区、辽东湾海域、北戴河附近海域、天津附近海域、黄河口三角洲海域以及莱州湾海域。观测站位分布,渤海区划及渤海水深如图1所示。
2 计算方法
罗斯贝变形半径在数学表达上,可以理解为:在地球旋转特征周期这一时间尺度上,长重力波传播的特征距离[11]。在纬度大于5°的海域,罗斯贝变形半径可以写为:
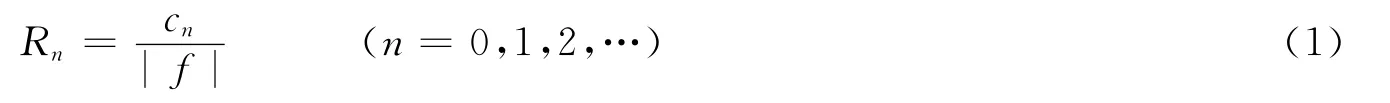
式中,f=2Ωsin(θ)是科氏参数;Ω为地球自转角速度;θ为地理纬度。当n=0时,c0为海洋中正压波的相速度,对应的R0为正压罗斯贝变形半径;当n=1时,c1为第一斜压重力波相速度,对应的R1为第一斜压罗斯贝变形半径。第一斜压罗斯贝变形半径在海洋环流理论方面起重要作用,是中尺度涡、沿岸射流和赤道流等的水平尺度[10],故本文主要研究第一斜压重力波相速度以及对应的第一斜压罗斯贝变形半径。通常如不特别说明,斜压罗斯贝变形半径均指第一斜压罗斯贝变形半径。
在不考虑底摩擦和风应力,引入平底、海面刚盖近似,及Boussinesq近似的假设下,稳定层化海洋水平大尺度波动的垂直结构满足:
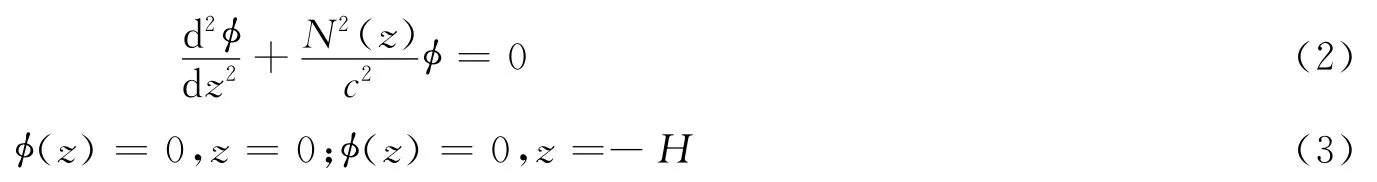
式中,H为水深;φ(z)为垂向速度分离变量后只与z有关的垂向函数;N(z)为Brunt-Väisälä频率,亦称浮性频率,忽略压缩性的影响,其表达式为:

式中,ρ表示密度;g表示重力加速度。
方程(2)及边界条件(3)组成了典型的Sturm-Liouville问题,求解罗斯贝变形半径,即转换成求解Sturm-Liouville本征值的问题[2]。对于连续层化的海洋,方程(2)对应的本征值是一组有序、非负的数列:。对应的本征函数为φ1(z),φ2(z),φ3(z)…,下标表示模态数(mode number)。cn表征第n模态斜压重力波相速度,由c1和科氏参数f便可确定第一斜压罗斯贝变形半径R1。
2.1 WKB近似
在求解由方程(2)及边界条件(3)组成的Sturm-Liouville问题中,WKB近似是一种快捷有效的方法[6]。其基本思想是把φ(z)写成下面的小参数幂级数的指数形式:
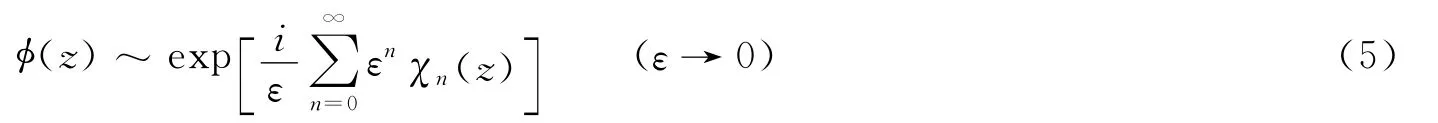
根据本文的情况,在小参数幂级数中引入虚数单位i。将式(5)代入方程(2)中,令ε的同次幂系数相等,可得递推方程组:

通过递推方程组求解χ0(z),χ1(z),代入到式(5)中,只保留幂级数显著的前两项,即可得出φ(z)的WKB近似解:
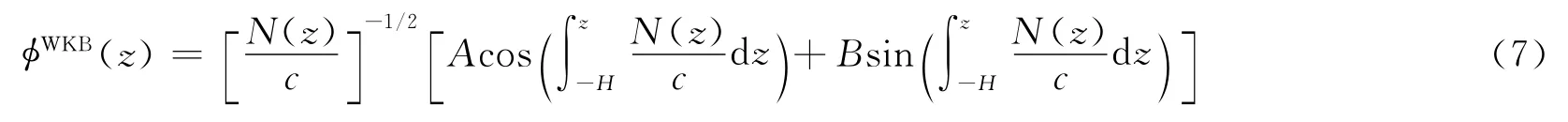
式中,A,B为任意常系数,代入边界条件(3)得:

即

当n=1时,通过式(8)和式(9)便可求解出第一斜压重力波相速度c1和第一斜压罗斯贝变形半径R1。
2.2 数值解法
数值解法是将本征值问题离散化后求解的过程。在相邻离散深度zk、zk+1上,利用中间密度梯度法(neutral density gradient method)[6],将现场密度绝热调整到中间深度ζk=zk+1/2(图2),然后估计浮性频率的平方N2(z):
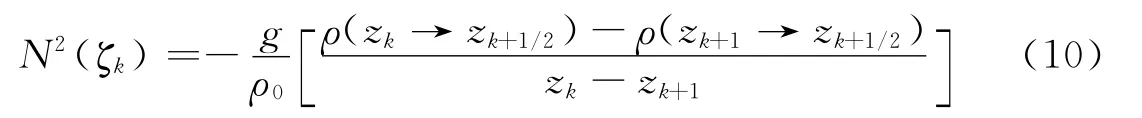
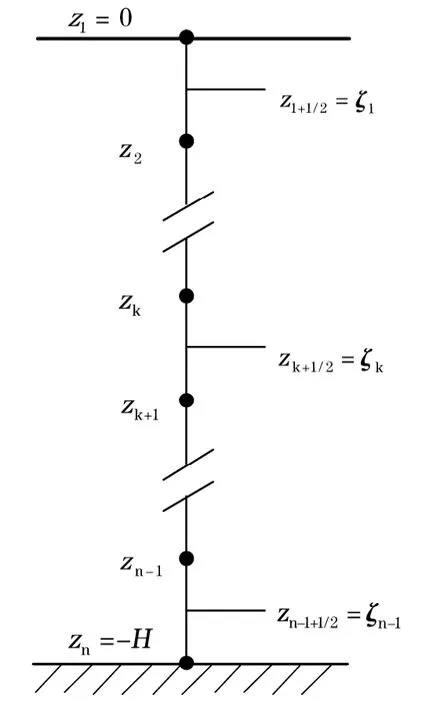
图2 数值解法中在离散深度上求解浮性频率的示意图Fig.2 Schematic diagram of vertical discretization in numerical method
据Chelton等[6]的建议,为了求罗斯贝变形半径,如果得到的N2(ζk)为负值,用相邻较浅深度ζk-1上的N2(ζk-1)代替;若N2(ζ1)为负值,令N2(ζ1)为10-8。
为了得到数值解,在深度ζk上离散本征值方程。首先,φ(z)在z=ζk(k=1,…,n-1)上进行泰勒展开:

通过式(11)求取φ(ζk-1)、φ(ζk+1),消除φ′(ζk)项后有:
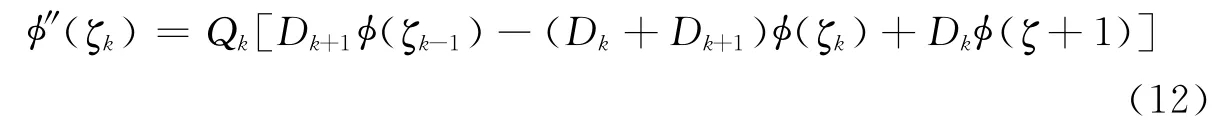
其中,

把式(11)代入到方程(2)中,得到n-1个离散方程,移项整理得:

式中,

根据本文的情况,定义边界条件为:

至此,将求解Sturm-Liouville本征值问题转换成求n-1阶矩阵特征值的问题[6]:

式中,
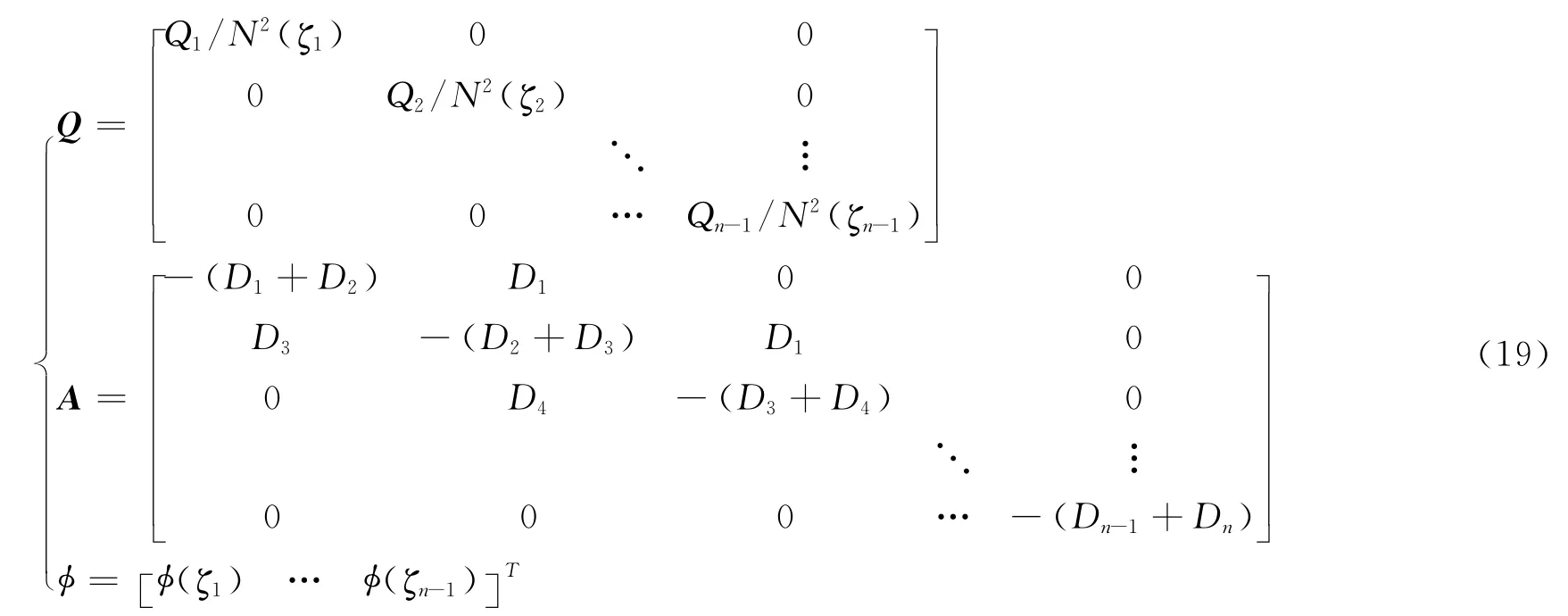
由式(18)可解出n-1个特征值μ1,…,μn-1,对应第一个特征值μ1,通过式(16)解出第一斜压重力波相速度c1和第一斜压罗斯贝变形半径R1。
3 结果分析
图3和图4分别给出了通过WKB近似和数值解法求出的渤海夏季第一斜压重力波相速度和第一斜压罗斯贝变形半径的分布。两种算法下得到的渤海夏季第一斜压重力波相速度和第一斜压罗斯贝变形半径的分布格局相似。斜压重力波相速度与斜压罗斯贝变形半径依赖于浮性频率的积分深度,即与实际水深有密切关系,故它们的分布与渤海水深分布大体一致,等值线呈耳状分布。在北戴河和长兴岛附近海域,斜压重力波相速度与斜压罗斯贝变形半径最大,然后向岸逐渐递减。在渤海中部等值线发生明显弯曲,在靠近渤海海峡内侧斜压重力波相速度与斜压罗斯贝变形半径出现一个小值,而与之对应在渤海中部以西出现一个大值,导致等值线呈NE-SW向倾斜的“S”状。

图3 WKB近似结果Fig.3 Result of WKB method
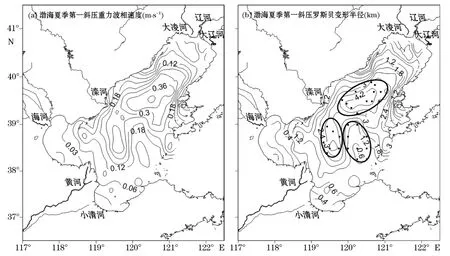
图4 数值方法计算结果Fig 4 Result of numerical method

表1 WKB近似计算得出的第一斜压重力波相速度和第一斜压罗斯贝变形半径Table 1 The first baroclinic gravity wave phase speed and Rossby deformation radius calculated by WKB method

表2 数值方法计算得出的第一斜压重力波相速度和第一斜压罗斯贝变形半径Table 2 The first baroclinic gravity wave phase speed and Rossby deformation radius calculated by numerical method
在WKB近似下,渤海夏季第一斜压罗斯贝变形半径的最大值出现在长兴岛附近海域,为3.13km,对应的斜压重力波相速度最大为0.28m/s;在莱州湾海域斜压罗斯贝变形半径和对应的斜压重力波相速度最大值仅为0.95km和0.08m/s;在辽东湾海域、北戴河附近海域、天津附近海域和黄河口三角洲海域,斜压罗斯贝变形半径和斜压重力波相速度的最大值分别为1.58,2.56,2.02和1.60km,以及0.15,0.24,0.18和0.14m/s。
在数值解法下,第一斜压罗斯贝变形半径与第一斜压重力波相速度的值均比在 WKB近似下的值大。最大值出现在北戴河附近海域,为4.72km和0.44m/s;次最大值出现在长兴岛附近海域,为4.51km和0.42m/s;在莱州湾海域斜压罗斯贝变形半径和斜压重力波相速度的最大值较小,分别为1.76km和0.16 m/s。在辽东湾海域、天津附近海域和黄河口三角洲海域的最大值分别为2.97,2.37,2.55km和0.28,0.22,0.23m/s。两种算法得出的第一斜压罗斯贝变形半径的比较见图5。

图5 两种算法得出的第一斜压罗斯贝变形半径的比较Fig.5 Comparison between the WKB approximation and numerical estimate R1 of the first baroclinic Rossby deformation radius
从图5可以看出,渤海夏季第一斜压罗斯贝变形半径在WKB近似下的结果总体低于数值解法求出的结果,同样的情况也出现在其它海区的相关研究中。Fennel等[7]和Osinski等[8]在波罗的海的斜压罗斯贝变形半径的计算中均表明,WKB近似的结果偏小于数值解,Fennel指出偏小10%~30%[7]。这主要是因为,WKB近似适用于浮性频率垂向变化较弱的情况。由式(9)和式(10)可以看出,在 WKB近似中,第一斜压重力波的相速度和第一斜压罗斯贝变形半径依赖于浮性频率随水深的积分,而在实际求解的过程中,将连续的海洋分为若干层处理,浮性频率一般取所在层的平均值,忽略了浮性频率的变化。故当浮性频率垂向变化较大,WKB近似计算误差较大。但在深海大洋中计算罗斯贝变形半径,WKB近似的结果偏大[6],在此不作详细讨论。
图3b和图4b中标出了斜压罗斯贝变形半径出现极值的区域,其中在北戴河和长兴岛附近海域的极大值区有13个站点,在渤海中部以西海域的极大值区有7个站点,而在渤海中部以东海域的极小值区有9个站点。根据这些站点的温盐数据,计算了极值区域的浮性频率的垂向分布,如图6所示。
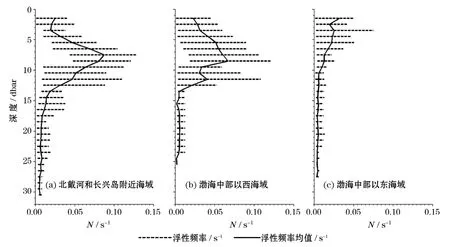
图6 渤海三极值区浮性频率垂向分布图Fig.6 Profile of Brunt-Väisäläfrequency in the three extreme areas
由图6可见,在北戴河和长兴岛附近海域,以及渤海中部以西海域,浮性频率的垂向分布较大,导致该海域较强的斜压性,因此计算得出的第一斜压罗斯贝变形半径在该海域出现极大值。而在渤海中部以东海域,浮性频率的垂向分布整体较小,计算得出的第一斜压罗斯贝变形半径在该海域出现极小值。
图7绘制了整个渤海夏季浮性频率的垂向分布。可见在水深8dbar附近浮性频率达到最大,达0.13s-1,这一深度也是渤海夏季跃层发生的深度。随着深度变大,浮性频率逐渐减小,到水深20dbar的附近,浮性频率降至约0.04s-1,因此可以看出,渤海夏季浮性频率垂向上变化较大,故在计算第一斜压罗斯贝变形半径的过程中,WKB近似的误差较大,建议采用斜压罗斯贝变形半径的数值解。

图7 整个渤海夏季浮性频率垂向分布图Fig.7 Vertical distribution of Brunt-Väisäläfrequency in the whole Bohai Sea
4 结论
本文利用渤海2006年夏季的温度和盐度大面观测资料,运用WKB近似和数值方法计算了渤海夏季第一斜压罗斯贝变形半径和第一斜压重力波相速度。结果显示,两种不同算法得出的斜压罗斯贝变形半径和斜压重力波相速度的分布格局相似,与渤海等深线分布大体一致。数值解法下,在北戴河和长兴岛附近海域,斜压罗斯贝变形半径较大,最大为4.72km,对应的斜压重力波相速度最大为0.44m/s;在莱州湾海域,斜压罗斯贝变形半径较小,最大仅为1.76km,对应的斜压重力波相速度最大为0.16m/s;在渤海中部斜压罗斯贝变形半径和斜压重力波相速度的等值线发生明显弯曲,在靠近渤海海峡内侧出现一个小值,而与之对应在渤海中部以西出现一个大值,导致等值线呈NE-SW向倾斜的“S”状。在辽东湾海域、天津附近海域和黄河口三角洲海域,斜压罗斯贝变形半径和斜压重力波相速度的最大值分别为2.97,2.37和2.55km,以及0.28,0.22和0.23m/s。
渤海夏季浮性频率的垂向变化较大,在水深8dbar附近浮性频率达到最大。在WKB近似计算渤海夏季第一斜压罗斯贝变形半径的过程中,因其依赖于浮性频率对水深的积分,得出的结果误差较大,其值低于数值解法求出的结果。
(References):
[1]XIONG X J.The circulation structure and mechanism studies on the China Seas[D].Qingdao:Ocean University of China,2013.熊学军.中国近海环流及其发生机制研究[D].青岛:中国海洋大学,2013.
[2]GILL A E.Atmosphere-Ocean dynamics[M].New York:Academic Press,1982.
[3]ALENIUS P,NEKRASOV A,MYRBERG K.Variability of the baroclinic Rossby radius in the Gulf of Finland[J].Continental Shelf Research,2003,23(6):563-573.
[4]EMERY W J,LEE W G,MAGAARD L.Geographic and deasonal distributions of Brunt-Väisäläfrequency and Rossby radii in the North Pacific and North Atlantic[J].Journal of Physical Oceanography,1984,14(2):294-317.
[5]HOURY S,DOMBROWSKY E,DEMEY P,et al.Brunt-Väisäläfrequency and Rossby Radii in the South Atlantic[J].Journal of Physical Oceanography,1987,17(10):1619-1626.
[6]CHELTON D B,DESZOEKE R A,SCHLAX M G.Geographical variability of the first baroclinic Rossby radius of deformation[J].Journal of Physical Oceanography,1998,28(3):433-460.
[7]FENNEL W,SEIFERT T,KAYSER B.Rossby radii and phase speeds in the Baltic Sea[J].Continental Shelf Research,1991,11(1):23-36.
[8]OSINSKI R,RAK D,WALCZOWSKI W,et al.Baroclinic Rossby radius of deformation in the southern Baltic Sea[J].Oceanologia,2010,52(3):417-429.
[9]GAN Z J,CAI S Q.Geographical and seasonal variability of Rossby radii in South China Sea[J].Journal of Tropical Oceanography,2001,20(1):1-9.甘子钧,蔡树群.南海罗斯贝变形半径的地理及季节变化[J].热带海洋学报,2001,20(1):1-9.
[10]CAI S Q,LONG X M,WU R H,et al.Geographical and monthly variability of the first baroclinic Rossby radius of deformation in the South China Sea[J].Journal of Marine Systems,2008,74(1-2):711-720.
[11]YU Z H,YANG D S,HE H Y,et al.Geophysical fluid dynamics[M].Beijing:China Meteorological Press,1996.余志豪,杨大升,贺海晏,等.地球物理流体动力学[M].北京:气象出版社,1996.

