一元三次多项式函数极值点的极值——拉氏乘数法和Mathematica 的全面实现

徐沥泉，史立新，周公贤

（1.无锡市教科院，无锡214001；2.无锡华罗庚研究会，无锡2140003）

0 引言

本文系2009 年一道高考全国卷数学试题压轴题所引发的思考。先看题目的表述：

文献[1-3]，都涉及到对2009 年全国卷I（理）22 题（下称考题）的研究与评论。题目是这样的：

设函数f(x)=x3+3bx2+3cx 有两个极值点x1和x2，且x1∈[- 1，0]，x2∈[1 ，2]。

（I）求b、c 满足的约束条件，并在坐标平面内，画出满足这些条件的点( b， c )的区域；

（II）证明：-10 ≤f( x2)≤-1/2。

略解（I）由题意推出b、c 的约束条件为：

满足这些条件的点( b， c )的区域为图1 中阴影部分并含其边界。

由于命题者对（II）的标准答案所给出的证明（此处从略）是“消去了系数b”而推出的。

结果；于是就有文献[1]的质疑：“为什么不消去c”？进而又有文献[2]和文献[3]等争鸣与评论。其实，“消b”正是运用了关系式f( x2，b ( c， x2))；而“消c”是运用了关系式f( x2，c ( b， x2))。由题设，点( b， c )虽约束在区域φ( b，c )中，但它们却可以是其中的任意一个点。实际上，这个看似关于要求f( x2)的一元三次多项函数的极值，却是一个关于二元函数在平面区域φ( b，c )下的条件极值问题。因为，x2是f'( x2)=3x22+6bx2+3c 的根，且x2∈[1 ，2]，故

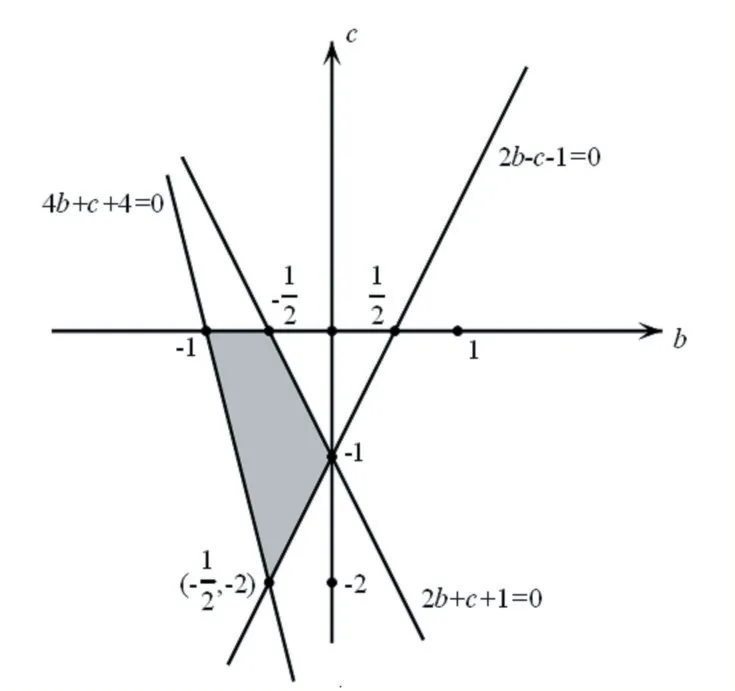
图1

一般说来，对诸如此类条件极值问题的处理，中学生只能运用一些特殊的解法，而大学生则会自然而然地运用一般的方法，即拉氏乘数法去求解[4]。但作为一个中学数学教师，不仅应该通晓初等数学，而且也应该了解其高等数学背景。尤其是高考试题中的那些把关题和压轴题，都具有明显的高等数学背景，它们对以后进一步深造来说是非常必须的，具有较好的选拔功能，同时也具有导学和导教功能。对这些问题，教师本身在思想上没有个底，要在平时引导学生获得较高的数学素养是困难的，而要在高考时转化为学生在考场上的能力更是不可能的。

F.克莱因（Felix Christian Klein，1849～1925）强调要用近代数学的观点来改造传统的中学数学内容，倡导“高观点下的初等数学”意识。在克莱因看来，基础数学的教师应该站在更高的视角（高等数学）来审视、理解初等数学问题，只有观点高了，事物才能显得明了而简单；有许多初等数学的现象只有在非初等的理论结构内才能深刻地理解。他的名著《高观点下的初等数学》，对我国从事数学学习和数学教育的广大读者具有较好的启示作用[5]。用拉氏乘数法并借助数学软件Mathematica 来审视这道高考压轴题，不仅不会有上述的质疑和争鸣，而且还能深刻地理解命题人是如何给出这道考题的题设条件的。

尽管多元函数求极值计算量较大，很多情况下手动计算难以实现。但应用数学软件不仅极大地降低了多元函数极值问题的求解难度，提高了教学效率，而且还能激发学生的学习兴趣，进而提高学生利用数学知识解决实际问题的能力。

以下介绍使用拉氏乘数法和Mathematica 对此问题的实现[6-8]。

1 预备定理（一元三次多项式函数的极值点公式）

先引入一元三次多项式函数的极值点公式。如所知，关于x 的一元三次多项式的一般形式为f(x)=ax3+bx2+cx+d，其中a、b、c、d ∈R，是多项式f(x )的系数，确保f(x )是3 次多项式。

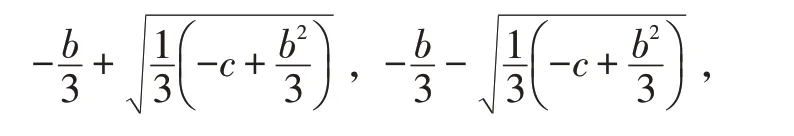
证明：我们先考虑形如f(x)=x3+cx 的较为简单情形。显然，当c ≥0 时，恒有：

f'(x)=3x2+c ≥0，故f(x )在( -∞ ， +∞ )上是增函数，无极值点；而当c<0，且x ∈( 0， +∞)时，

下面，我们考虑一般情形，不妨设：

a=1，f(x)=x3+bx2+cx+d。

否则只要改变项的系数而已。考虑等价式：

右边的导函数为：

2 极值点的极值

对于常系数的一元三次多项式，它的极大值点和极小值点是确定的、固定的，其本身并无极值可言；然而，对变系数的一元三次多项式，随着它们的系数在某一个范围内变化，它的极值点也随之改变，相对前者而言的常数已成为变量，因而就有所谓的极值存在。

下面，我们利用数学软件Mathematica 给出那道考题的动态图像，指令为：

Manipulate[Plot[x^3+3*b*x^2+3*c*x，{x，-2，2}，Plot Range→All]，{{b，-1}，-1，0}，{{c，-2}，-2，0}]

它表示f(x )的系数b、c 可以在区间b ∈[- 1， 0] 和c ∈[- 2， 0] 上变动，只需滑动图2 左上方b、c 轴上的小方块，就可以得到你所需的状态图，图2 和3 给出的是当b、c 都在初始时刻和取中时刻的图像。

图2 b，c在初始时刻

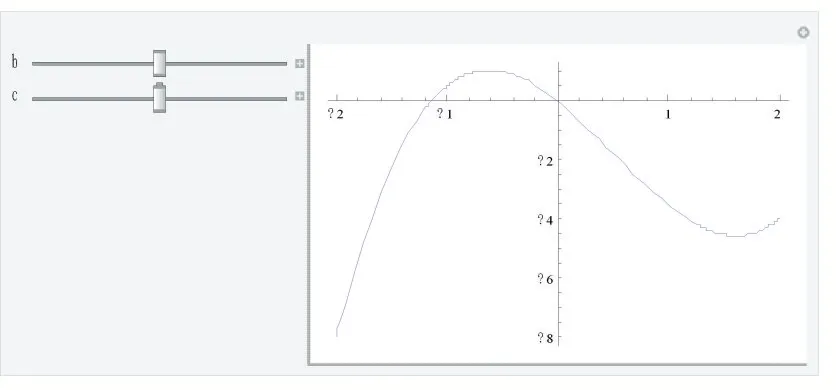
图3 b，c在取中时刻

图4

图5 f(x)min=-10

从上面图像也可以看出，当b、c 在给定范围内变化时，f(x )的2 个极值点落入区间[- 1， 0] 和[1 ， 2]。由此可见，那道高考压轴题的题设条件可由此得来。

那么，一般说来，如何求出变系数一元三次多项式函数极值点的极值呢？仍以f(x)=x3+3bx2+3cx 为例，请看下文。

3 拉格朗日乘数法和Mathematica的实现

由上述定理知，函数：

现要求函数：

简记为f(b，c)()1。

完全类似地，由二元函数：

简记为f(b，c)(2)。

我们可以考虑另一个极值点x1的最值f( x1)，当然也是在区域Φ( b，c )上。这里在( b，c )∈[- 10 ，10] 时 我们给出它们的图像，图6 和图7，姑且称之为立方抛物面。

图6

图7

图6 和图7 的Mathematica 指令分别为：

则：

两式相减并化简，得：

两边可约去x2并代回它和式（1），得：

化简后得：

不合题意，故f 在区域Φ 内部无驻点，亦即阴影区域内的任意一点都不可能是驻点。因此，它如果有驻点，应落在它的4 条边界线上，现考虑边界，应用多元函数求条件极值的拉格朗日乘数法，有形式：

人工计算工作量有点大，我们还是借助Mathematica[9]。通过有效尝试，先考虑约束条件-4b-c-4 ≤0 和2b-c-1 ≤0，命：

求F 对b， c， δ1，δ2的偏导数，得：

求F 对b， c， δ1，δ2的偏导数指令：

解下面这个驻点方程组：

求解驻点方程组的指令：

再考虑约束条件2b+c+1 ≤0 和c ≤0，命

求F 对b， c， δ3，δ4的偏导数，得：

令其为零，解下面的方程组：

Mathematica 指令与上类同，此处从略。以上求得的2 个可能极值点，恰好就是f 在区域Φ 的2 个顶点和把它们代入f(b，c)(1) 所得的值，与 另2 个 顶 点A( -1， 0 )、C( 0， -1) 代 入 f(b，c)(1)的值：

比较可知其最小值和最大值为：

同理可求在区域φ( b，c )上另一个极值点x1的最值，这里只给出结果（可供读者练习）：

图8

图9

其Mathematica 指令分别为：

注：关于上述高考试题的最新文献“二维含参型一元三次函数极值点的最值”[10]，全面解剖了国家考试中心所给出的题设与标准答案，并在初等数学范畴中给出了漂亮的结果。

4 结语

综上所述，我们把2009 年全国高考数学卷I（理）22 题第（II）小问的证明：转化为求二元函数f(b，c)()1：

此外，还给出了它们的直观图像，如图8 和9 所示，从中可以观察到这2 个二元函数在区域φ上是怎么发展变化的。

上述第2 部分的内容与图示，则是说明了这道高考题的出处，即命题者的依据所在。

本文从2009 年全国卷I（理）22 题的标准答案所引发的质疑与评论作为出发点，指出了其本质上是属于二元函数的条件极值问题，把它纳入到拉格朗日乘数法和数学软件Mathematica 的知识结构中，全面实现了对它的求解与证明。这至少说明了以下两点：

其一，正如F.克莱因所言，只有观点高了，事物才能显得明了而简单，许多初等数学的现象只有在非初等的理论结构内才能深刻地理解。相对说来掌握了更高一级的一般解题方法之后，就不必耗费过多的时间和精力去追求那些特殊的解题技能与技巧了；其二，本来那些靠人工计算和操作难以解决或无法解决的数学问题，如今应用计算机编程和专用应用软件就可以如愿以偿地得以实现。