基于变量节点稳定性的SCMA 多用户检测算法
范鹏,李旭东
(西华大学理学院,成都610039)
0 引言
随着第四代移动通信系统(The Fourth Generation Mobile Communication Systems,4G)的大规模商业化及其技术的不断成熟,第五代移动通信系统(The Fifth Generation Mobile Communication Systems,5G)已成为全球研发的焦点[1-2]。目前,我国工信部已正式发放5G 商用牌照,与4G 相比,5G 在频谱资源利用率和终端设备接入量均有很大的提高。非正交多址接入技术[3](Non-Orthogonal Multiple-Access,NOMA)拥有频谱效率较高的特点,在5G 通信中有着广泛的应用。作为NOMA技术的一种,SCMA[4-5]利用码本的稀疏性能够连接大量不同的终端用户,并同时为终端用户服务。在发送端,每个用户将数据比特直接映射为SCMA 码本中的多维码字,多个用户的码字进行叠加,使得同一频谱资源上可以承载多个用户,大幅度地提高了系统容量。在接收端,接收信号是多个用户码字和噪声的叠加,需要对接收信号通过多用户检测(Multi-user Detection,MUD)技术来实现用户译码。
利用SCMA 码序列的稀疏性,在接收端使用复杂度相对较低的消息传递算法(Message Passing Algorithm,MPA)[6]进行译码。该系统中多个用户共享频率资源,来成倍提高系统容量和频谱利用率,同时,基于MPA 的MUD 极大地降低了联合最优最大后验概率(Maximum-A-Posteriori,MAP)的复杂度。但原始的MPA 算法复杂度依然很高,特别是用户码本大小增加以及同一资源的用户数增多时,其计算复杂度呈指数增长。为了降低原始MPA 算法复杂度,文献[7]通过每次迭代计算未判决用户的码字可信度,将码字可信度满足门限条件的用户提前译码来降低算法复杂度;文献[8]提出函数节点在每次迭代中以串行方式,将已更新的消息立即传递到当前迭代中,从而降低算法复杂度;文献[9]引入权重因子改变每个叠加星座点的初始概率,加快了迭代过程的收敛速度,降低了算法复杂度。此外文献[10-12]通过不同的方法来降低算法的复杂度。
为了降低原始MPA 算法的复杂度,本文提出了一种变量节点稳定性判断的方法。在每一轮迭代更新中,找出未译码用户变量节点最大可信度的位置,若用户所有变量节点最大可信度的位置相同,且在当前迭代和上次迭代中各变量节点最大可信度的位置也相同,则对用户提前译码。仿真结果表明,本文所提算法在收敛速度和BER 性能上,优于门限MPA 算法和原始MPA 算法。在算法复杂度上优于原始MPA 算法。
1 系统模型
1.1 SCMA系统模型
假定一个上行多用户SCMA 通信系统共有K 个资源块,每个用户占用资源数为N(N

图1 上行SCMA多用户通信系统模型(J=6,K=4)
SCMA 码的总结构可以由对应的因子图及因子图矩阵F=(f1,f2,…,fJ)来表示。当且仅当Fk,j=1 时,用户j 占用资源块k。稀疏矩阵的SCMA 因子图及其矩阵如图2 所示。
当J 个用户同时接入时,接收信号可表示为:

其中,xj=(x1,j,x2,j,…,xK,j)T表示第j 个用户发送的码字,hj=(h1,j,h2,j,…,hK,j)T表示第j 个用户的信道有效向量,n=(n1,n2,…,nK)表示信道噪声且n ~cN(0,σ2I)。第k 个资源块接收信号为:


图2 SCMA码本因子图及其矩阵
1.2 原始MPA算法[5]
假定已知接收信号y 和信道矩阵H=(h1,h2,…,hJ),用MAP 算法来检测用户数据X=(x1,x2,…,xJ),如式:

MPA 算法是利用因子图求边缘概率分布的一种迭代算法,在算法迭代过程中,因子图的变量节点和函数节点之间通过边传递消息,每次消息传递后,根据一定的计算准则更新每个节点存储的可信度值,以便计算下一次传递的外部信息。在多次消息迭代更新后,获得一个关于所有用户码字的边缘概率分布,以此概率分布作为判决量判决输出结果,从而判断出每个用户发送的码字。MPA 算法利用了码本稀疏性的特征,其算法复杂度为O(Mf)(f 表示每个资源上叠加的用户数,f 第一步,初始化,即SCMA 接收机在迭代开始时,假设每个用户发送各码字的概率相同,即: 第二步,由式(5)和式(6)分别更新函数节点和变量节点的消息,即: 其中,εk表示占用资源k 的用户集合,l ∈εk/j 表示从集合εk中除去用户j,目的是获得用户j 的外信息,normalize()· 表示归一化。式(7)涉及信道传递函数,即: 第三步,迭代步数加1,重复第二步的操作,直到迭代次数达到最大迭代次数Tmax,对用户码字进行译码。 虽然MPA 算法极大地降低了MAP 的复杂度,使其硬件实现成为可能,但是当系统用户数过多、用户码本尺寸过大或信号经历快衰落时,MPA 复杂度依旧很高,不能满足高质量的通信需求。 为了降低SCMA 多用户检测的复杂度,本文提出了基于变量节点稳定性的多用户检测算法。在每一轮迭代更新中,找出未译码用户变量节点最大可信度的位置,若用户所有变量节点最大可信度的位置相同,且在当前迭代和上次迭代中各变量节点最大可信度的位置也相同,则对用户提前译码。这使得在保证降低算法复杂度的同时,提高了用户译码的可靠性。 首先我们根据用户是否已经提前译码,将用户分为两个集合,译码集φ 和非译码集ψ。在算法初始化阶段,所有用户都未译码,即所有用户都在非译码集ψ之中。在每次消息迭代更新后,由式(9)找出第t 次迭代时用户j 在资源块k 上码字可信度最大的位置,即: 根据式(8)可知,用户发送码字的可信度等于该用户所有资源上变量节点的乘积。当检测到任意用户j的变量节点码字最大可信度位置有不同时,这说明用户j 的变量节点还未完全收敛,若此时直接将用户j 进行译码,多用户检测的误码概率将会大大增加。因此当用户j 的变量节点码字最大可信度位置相同时,即,用户j 译码的准确性将有所提高。为了进一步提高用户译码的准确性,这里给出变量节点稳定性判断定义:在算法迭代过程,若用户j 的某一变量节点在当前迭代和上一次迭代中,检测到最大码字可信度的位置为同一位置,即,则用户j 的这一变量节点趋于稳定。只有当用户j 的所有变量节点码字可信度均最大且满足稳定性条件时,才将用户j 提前译码,并将该用户从非译码集ψ 移出放入译码集φ。若运行到最大迭代次数后若非译码集ψ 中仍有用户存在,由式(10)继续对剩余非译码集ψ 中用户进行译码,即: 从而确定所有用户的码字。 MPA 算法过程主要分为消息更新和码字检验两个阶段,其算法复杂度主要体现在消息更新上。本文算法仅仅在每次消息更新迭代结束后,判断用户在后续迭代中是否继续消息迭代更新,这个过程并没有破坏用户消息更新环节。比较原始MPA 算法[6]、门限MPA算法[7]和本文所提到的算法复杂度,只需要比较不同算法在迭代过程中需要的乘法运算数目即可。原始的MPA 算法所需的乘法个数为[13]: 其中dr和dc分别表示每个资源块上的用户数和每个用户占用的资源块数。由式(11)可知,在用户码本不变的情况下,影响本文算法复杂度的参数为用户数和迭代次数。在本文算法中,因噪声存在随机性,不能给出具体算法复杂度的公式表达。在每次迭代过程中,用户数随着部分用户提前译码而逐步减少,特别是当信噪比越高时,所有用户未达到最大迭代次数就能被全部译码,故所提算法复杂度低于原始MPA 算法的复杂度。本文算法与门限MPA 算法相比,将用户码字提前判决条件从用户码字可信度降低到变量节点码字可信度,减少了提前判断用户码字时各变量节点的软信息损失,从而提高了BER 性能。 通过仿真对比原始MPA 算法[6]、门限MPA 算法[7]以及本文提出的算法,验证本文算法BER 性能,收敛速度和算法复杂度。由于门限MPA 算法在门限较高时近似原始MPA 算法,仿真只选择门限为Th=20 来进行对比。在仿真中,用户数为6,资源块数为4,最大迭代次数为6,信道模型为AWGN。 图3 中可以看出,在迭代次数为2 时,本文提出的算法性能优于门限MPA(Th=20)和原始MPA 算法。在Eb/N0=11 时,迭代次数为2 的门限MPA(Th=20)和原始MPA 算法的EBR 值分别为0.0039 和0.0036,而本文算法的BER 值为0.0012,特别是Eb/N0>11 时,可以看到本文迭代2 次的EBR 性能明显优于门限MPA(Th=20)的迭代4 次的EBR 性能。图3 中还可以看出,本文算法迭代4 次的BER 性能几乎和原始MPA算法迭代4 次的BER 性能相当,在Eb/N0=13 时,这两种算法的BER 值相差仅为0.2×10-4。由于本文算法每次迭代后,已被译码的用户不再继续参与到后续迭代的消息更新中,故本文算法和原始MPA 算法相比不仅能保证BER 性能,同时也能大幅度的降低算法的复杂度。 从图3 可以看出,在迭代次数为2 时,本文提出的算法的码字收敛速度优于门限MPA(Th=20)和原始MPA 算法。从图4 可以看出,在为11 和13 时,本文算法迭代3 次就趋于收敛,而门限MPA 算法和原始MPA 算法至少要迭代5 次才趋于收敛。本文所提算法的收敛速度明显优于门限算法和原始MPA 算法。 图3 不同算法不同迭代次数的BER对比 图4 各算法收敛速度对比 为了对比各算法之间的复杂度,在仿真过程中统计出各算法在不同、不同迭代次数下的平均乘法次数。在Eb/N0=13,迭代次数为4 时,本文所提算法、门限MPA 算法(Th=20)和原始MPA 算法的平均乘法次数为9974、6171 和18456,本文算法和门限MPA算法(Th=20)相比复杂度高61.6%,但BER 性能高68.7%,和原始MPA 算法相比复杂度只有原始MPA 算法的54%,BER 性能降低13.8%。 为了降低SCMA 系通信统中多用户检测算法的复杂度,本文提出了基于变量节点稳定性的多用户检测算法。该算法在收敛速度和BER 性能方面明显优于门限MPA 算法,与原始MPA 算法相比,在BER 性能几乎不变的前提下,大大降低了算法的复杂性。因此,本文所提算法具有较高的实用性。

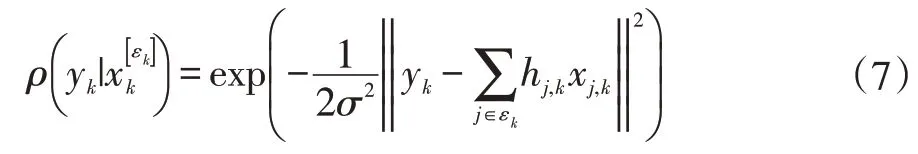

2 本文算法
2.1 变量节点稳定性的多用户检测算法


2.2 复杂度分析

3 仿真分析
3.1 BER性能比较
3.2 收敛速度分析


3.3 复杂度对比
4 结语

