一种5G系统自适应快速SCL极化码译码算法
汪晓雅,席 兵,高锦盟 ,邓炳光
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆邮电大学 光电工程学院,重庆 400065)
0 引言
1 极化码基本原理
1.1 极化码编码
与其他信道编码技术相比,极化码最大的特点是信道极化。信道极化后,在容量接近于1的信道上传输信息。通常使用巴氏系数算法、高斯近似算法(Gaussian Approximation,GA)、信道退化算法、极化重量(Polarization Weight,PW)算法和蒙特卡罗算法来构造极化码[10]。在编码过程中,通过计算相关参数得到各极化信道的可靠性,然后用前K个可靠性高的信道来传输信息比特,其余N-K个传输冻结比特[11]。极化码的编码过程描述如下:
(1)
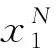

(2)
GN=BNF⊗n,n=lbN,
(3)
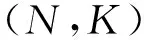
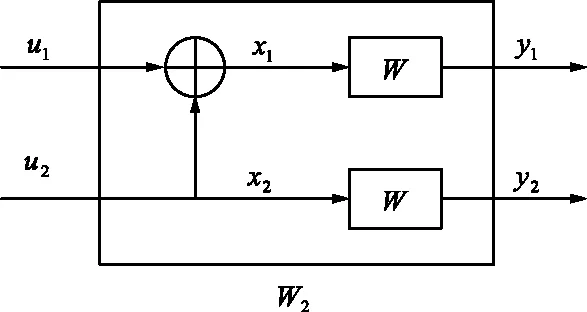
图1 极化码N=2Fig.1 Polar code with N=2
1.2 SC和SCL译码算法
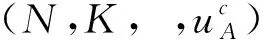
(4)

(5)
SCL译码器[3]内部并行地放置了L个SC译码器,在SC译码的串行过程中,SC译码器对每个信息位保留0与1,因此, 每条译码路径分裂为2条路径, 并更新路径度量(Path Metric,PM)来选择最佳L个候选,第i步的第l条路径对应的PM定义为:
(6)
PM反映了每条路径的可靠性,在算法最后,输出PM最小的路径。对于CA-SCL算法,选择CRC校验成功的结果,如果均未成功,则输出PM最小的路径。本文在仿真过程中均使用CRC-Polar级联码,编译码过程如图2所示。

图2 CA-SCL的编译码过程Fig.2 Encoding and decoding process of CA-SCL
1.3 FSCL译码算法
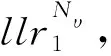
R0码是只有冻结比特,没有信息比特的极化码[18];Rep码只有最后一位信源比特是信息比特,其余都是冻结比特[18];SPC码只有第1位信源比特是冻结比特,其余都是信息比特[18];R1码[19]所有信源比特都是信息比特。长度N=32,K=16,使用GA在Eb/N0=2.5 dB时构造的极化码结构如图3所示,图中黑色代表信息比特,白色代表冻结比特,灰色是混合节点。
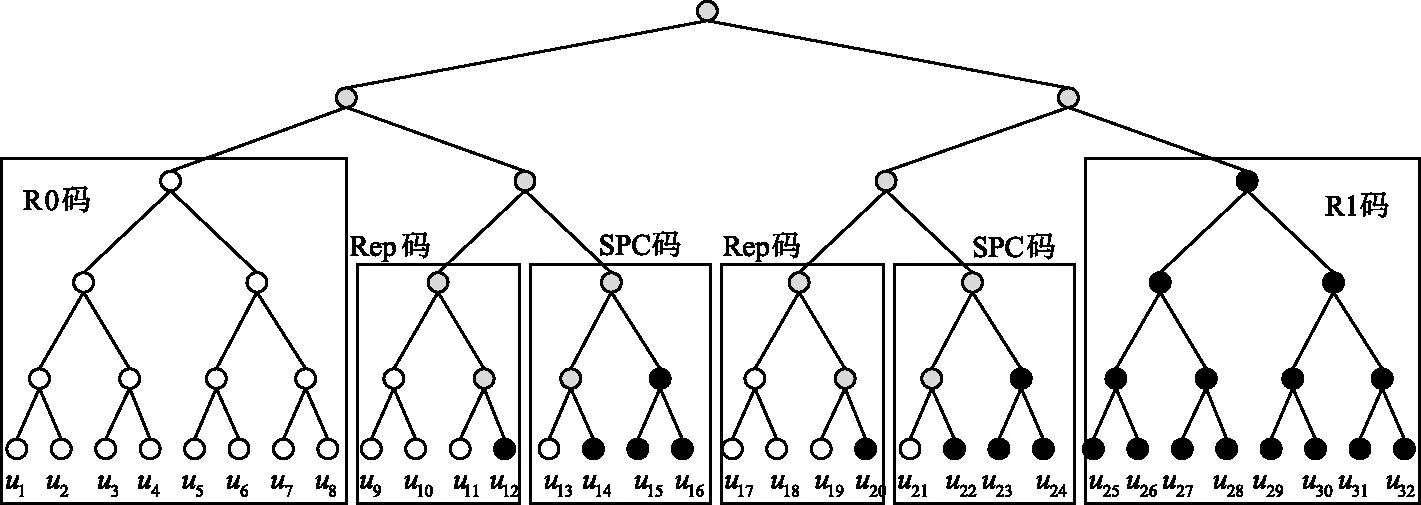
图3 N=32,K=16的极化码结构Fig.3 Polar code structure with N=32,K=16
2 AD-FSCL译码算法
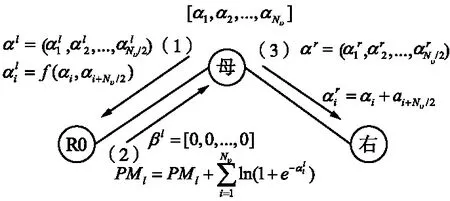
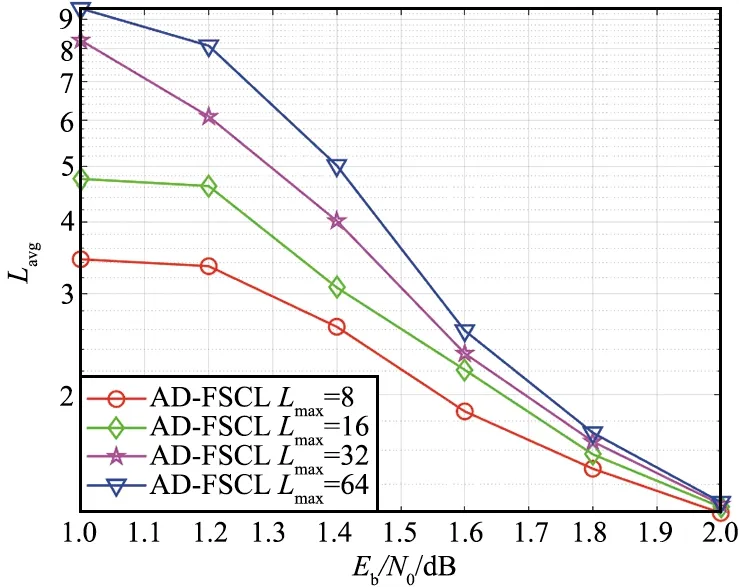
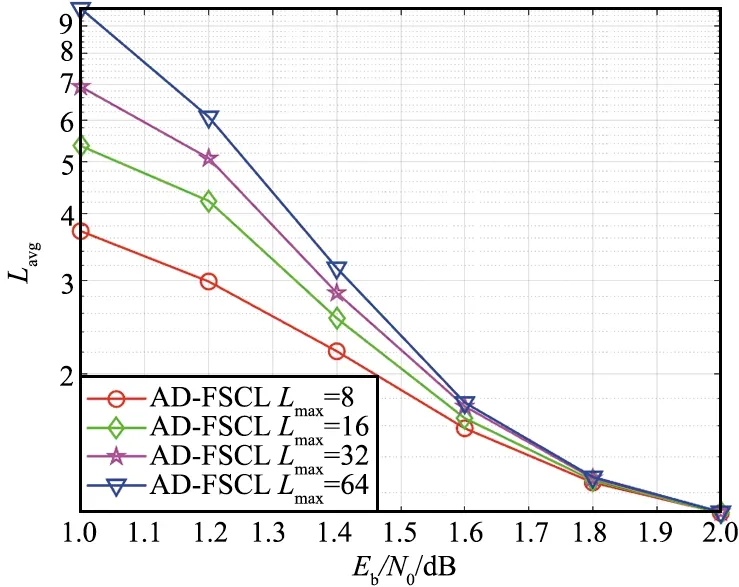
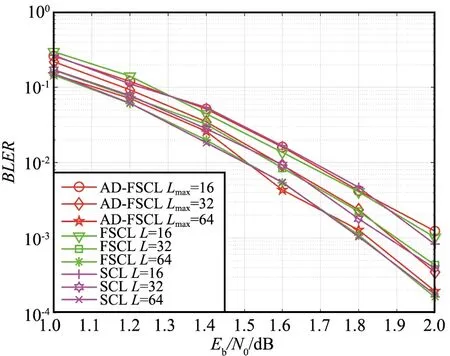
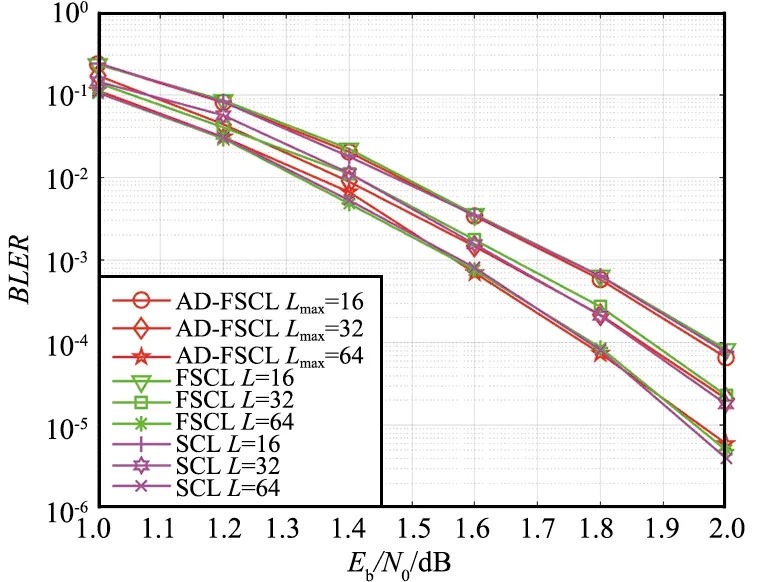
对于大多数接收到的信号,具有很小L的SCL译码器就可以译码成功,只有极少数信号需要很大的L才能译码成功[5]。为了降低FSCL译码算法的复杂度,提出的AD-FSCL译码算法动态地改变L的值至Lmax,译码成功时,如果L 本文提出的AD-FSCL译码算法首先设置列表初始值Linit=1,然后从Linit开始进行快速译码。若译码结果通过CRC校验,则译码成功;否则,将列表数量迭代增加L→2L,重新对接收信号进行快速译码;重复上述操作直到有译码结果通过CRC校验或列表数量超过最大列表数Lmax。AD-FSCL算法流程如图4所示。 图4 AD-FSCL算法流程Fig.4 Flow chart of AD-FSCL 算法的具体步骤如下: ① 使用GA算法构造极化码; ② 识别4种特殊节点的结构; ③ 极化码编码并计算接收信号的LLR; ④ 设置列表数量的初始值为L=Linit; ⑤ 对4种不同的特殊节点进行对应的FSCL译码; ⑥ 若译码结果通过CRC校验,则译码成功,结束算法; ⑦ 若译码结果未通过CRC校验,则迭代地增加列表数量L=2L; ⑧ 若L≤Lmax,返回重新进行FSCL译码; ⑨ 否则L>Lmax,译码失败,结束算法。 其中,R0节点、Rep节点、R1节点以及SPC节点快速译码的具体过程,在下文中介绍。 在SCL译码器(列表数量为L)中任取一个激活的SC译码器SCl(1≤l≤L),当SCl译码器的译码过程运行到一个R0节点时,由于R0节点中都是冻结比特,不存在任何路径克隆[18],计算R0节点对应的LLR序列,再把PMl(SCl在R0译码前的路径度量值)加上惩罚值,长度为Nυ的R0节点返回长度为Nυ的全0比特值。对于每一个激活的SC译码器都执行上述操作,R0节点的FSCL译码就完成了。R0节点的FSCL译码过程如图5所示。 图5 R0节点的FSCL译码Fig.5 FSCL decoding of R0 nodes 图中,α表示LLR,αl表示左侧后代节点的LLR,αr表示右侧后代节点的LLR,β表示部分和序列,βl表示左侧后代节点的部分和序列,βr表示右侧后代节点的部分和序列。f运算近似表示为: f(α1,α2)≈sign(α1)sign(α2)min{|α1|,|α2|}。 (7) 因为Rep节点存在路径克隆,所以译码比R0的译码稍微复杂一点。Rep节点的FSCL译码过程[18]如图6所示。 图6 Rep节点的FSCL译码Fig.6 FSCL decoding of Rep nodes (8) 矩阵的第1行第s(1≤s≤S)列表示SCis保存的全0序列PM值,第2行第s(1≤s≤S)列表示SCis保存的全1序列PM值,激活的译码器是哪些,每次译码时都不同。找到其中最小的min{L,2S}个值,保存其对应的序列,此时,每个译码器的状态都不一定相同[17]。 R1节点的快速SCL译码过程[19]如图7所示。对于一个激活的SC译码器SCl(1≤l≤L),路径度量为PMl,算出R1节点的LLR序列α1,α2,…,αNυ,直接对其进行硬比特判决得到β1,β2,…,βNυ。β1,β2,…,βNυ是α1,α2,…,αNυ的最大似然译码结果,β1,β2,…,βNυ对应的路径度量不改变。通过翻转β1,β2,…,βNυ中的一些比特得到α1,α2,…,αNυ的一些次最大似然译码结果,对翻转的比特βi对应的PM加上惩罚值|αi|。对|α1|,|α2|,…,|αNυ|进行升序排序得到|αi1|,|αi2|,…,|αiNυ|,那么除了PMl,最小的可能PM值就是PMl+|αi1|,对应的比特序列是β1,…,βi1⊕1,…,βNυ,找到前L个最小的PM以及对应的序列。对于已经激活的S个译码器,操作过程如图7所示,虚线框中是没有被选中的结果。 图7 R1节点的FSCL译码Fig.7 FSCL decoding of R1 nodes 对于已经激活的S个译码器,如图8所示,i1,i2指示第一次分裂,每个激活的译码器根据上述2种情况进行分裂,只保存前L个最小PM的分支,虚线框中是没有被选中的分支。若某个译码器的分支没被选中,则接收其他译码器复制的数据。 图8 SPC节点的FSCL译码Fig.8 FSCL decoding of SPC nodes 在仿真过程中,本文的仿真实验参数设置为:信道环境采用AWGN环境,调整方式为BPSK,码率为0.5,构造算法为GA,CRC长度为16。 首先对AD-FSCL译码算法的复杂度进行实验,用译码成功时的列表平均值Lavg表示复杂度。在N=1 024和N=2 048时,分别使Lmax=8,Lmax=16,Lmax=32,Lmax=64,将L的初始值设置为Linit=1,仿真实现AD-FSCL译码过程。每次译码成功时,记录L的值,并计算L的平均值Lavg,如图9和图10所示。 图9 译码成功L的平均值(N=1 024)Fig.9 Average value of L for successful decoding (N=1 024) 图10 译码成功L的平均值(N=2 048)Fig.10 Average value of L for successful decoding (N=2 048) 仿真实验表明,Eb/N0越小,Lavg值越大;Eb/N0越大,Lavg值越小,译码成功的列表平均值Lavg随着Eb/N0的增加而降低,在Eb/N0=2 dB时,Lavg趋近于1,并且,译码成功的Lavg均远小于Lmax,列表值降低,路径排序的复杂度就会降低,因此,算法译码复杂度降低。 在L=16,L=32,L=64时,分别对SCL译码算法、FSCL译码算法、AD-FSCL译码算法的BLER性能进行比较,如图11和图12所示。其中,图11是在码长为1 024时的仿真实验,图12是在码长为2 048时的仿真实验。仿真结果表明,在L相同时,3种译码算法的曲线几乎重合;3种译码算法的BLER均随着Eb/N0的增加而降低;3种译码算法的BLER也随着L的增加而变好,并且,3种译码算法在Eb/N0相同的条件下,BLER几乎一致。显然AD-FSCL译码算法在没有BLER性能损失的前提下,可以降低译码的复杂度。 图11 算法的BLER性能比较(N=1 024)Fig.11 BLER performance comparison of algorithms (N=1 024) 图12 算法的BLER性能比较(N=2 048)Fig.12 BLER performance comparison of algorithms(N=2 048) Polar码优越的性能使其成为5G系统控制信道的编码方案,其编译码算法也随之成为研究热点,为此本文探索了Polar码的译码算法。本文提出的AD-FSCL译码算法,与FSCL和SCL算法相比,可以在保持BLER性能不变的情况下降低译码复杂度,具有显著的性能增益。未来将对本文提出的创新算法进行硬件实现,从而商用。之后将侧重于Polar码在通信其他领域的研究。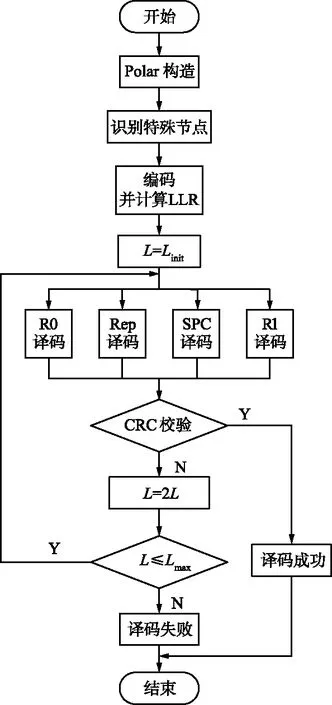
2.1 R0节点的FSCL译码
2.2 Rep节点的FSCL译码

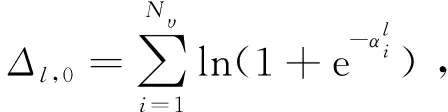
2.3 R1节点的FSCL译码

2.4 SPC节点的FSCL译码

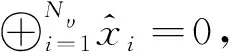
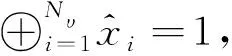

3 仿真分析
4 结束语

