波利亚在三角积分零点实性上的工作研究
王全来
(天津师范大学计算机与信息工程学院,天津 300387)
1 引言
波利亚在三角积分零点实性上的工作散见于一些数学理论著作中,如莱文 (J.Levin)的“整函数零点分布”[1](1964).目前见到的涉及波利亚此方面工作的重要文献,国外有两篇,国内尚未见到.一篇是迪米夫 (K.Dimitrov),鲁塞夫 (P.Rusev)的“整傅立叶变换的零点”[2](2011).但由于该文不是针对波利亚的工作进行研究,因而对波利亚的文章未能全部且系统解读,只涉及了波利亚的6篇文章,对他的思想演变过程和影响也未能深入探讨.由于作者的著作目的和时间所限,只引用了4篇2000年之后的文献,且相关文献引述不够全面,如沃克 (P.L.Walker)的“某些三角积分的零点”[3](1988)就未在此列.另一篇是约拉托(G.Iurato)的“黎曼Zeta函数理论的一些历史概况”[4](2013),该文只涉及了波利亚的4篇文章.他更未能对波利亚的工作进行系统研究.本文在前人工作的基础上,对波利亚的工作进行深入探讨,补充了一些重要文献,较为系统地研究波利亚的工作和蕴含的重要思想,藉此梳理与波利亚工作有关的三角积分零点实性理论的发展脉络.
2 波利亚工作的研究背景
三角积分零点实性问题是古老方程理论问题的一个现代变形,其产生于对黎曼猜想的研究.1859年,黎曼发表“在给定大小之下的素数个数”的论文.该文内容深刻,文笔简练,忽略了许多证明.在20世纪初这导致兰道,哈代的批评.他们评论道,黎曼只会做猜想,对于证明几乎不问津.这种论点在1932年由赛格尔(C.L.Siegel)改变.赛格尔在哥廷根大学花了两年的时间研究黎曼遗留的数学笔记,发表了相关论文,澄清了有关事实[5].
黎曼将素数分布问题归结为函数问题,现称为黎曼ζ(s)函数.ζ(s)作为实变量函数由欧拉引入,而作为复变量函数由黎曼引入.黎曼简要地断言了该函数的一些重要性质,其中有一断言至今未决,现称为黎曼猜想.黎曼猜想是指ζ(s)的所有非实根位于临界线上.黎曼给出

从整函数理论出发考虑关于(s−1)ζ(s)或类似函数的研究由阿达玛在皮卡的指导下于1892年完成的博士论文中创立.阿达玛的目的是把整函数理论应用于ζ(s)的研究,并为此完成三篇论文.胡尔维兹研究了阿达玛的这些论文,深受影响,并把有关研究结果第一个告知波利亚.波利亚和胡尔维兹关系很好,在1918年论文中称他是可尊敬的学者.他整理其数学遗稿,并在1933年出版了全集.波利亚受他在ζ(s)上工作影响很大,并继承他的有关思想.
延森(J.Jensen)在1911年的第二届数学家大会上许诺将发表关于将代数函数理论方法用于黎曼函数的论文.这一点可从其论“方程理论研究”[6](1913)的简短前言中得到证实.延森计划发表5篇包含他在复分析和代数方面的研究结果.延森在第188至189页上给出了计划论文第五篇题为“阶是1的函数类,特别是黎曼函数”的摘要,处理
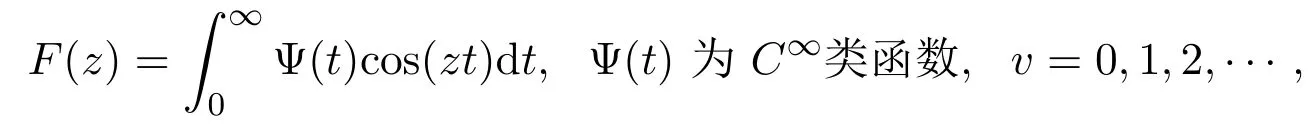
在C的每个边界子集上有
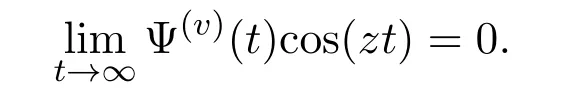
延森指出,这类函数的重要性归于黎曼ξ函数有一个上述形式的表示.他得到如下结果,F(z)只有实根,当且仅当

只有实根,p=1,2,3,···.很遗憾,未发表.
除受胡尔维兹、延森的思想影响外,波利亚也受到外尔和兰道的影响.外尔在1911-1914年间发表了一系列关于在某紧致域中拉普拉斯特征值的渐近分布的文章,激励波利亚提出用物理方法解决黎曼猜想的思想.阿文达尼奥(A.C.Avendaño)在2014年的论文中指出,波利亚在哥廷根向兰道学习解析函数论期间,在1914年的一天,兰道问波利亚“你知道黎曼猜想是对的物理原因吗?”波利亚的回答是,“若(z)的非实根和物理问题有关,黎曼猜想等价于物理问题的特征值为实的”[7].这个想法称为希尔伯特-波利亚猜想,尽管他们并未发表任何与该想法相关的成果.但在当时没有证据能够支持这种思想.塞尔伯格(A.Selberg)在“调和分析”(1956)中对此有所论及,但支持希尔伯特-波利亚猜想的第一个例子出现在蒙哥马利(H.L.Montgomery)的工作中.1971年秋,他在假设黎曼猜想正确的情况下,证明关于黎曼函数零点间距的统计性定理[8].希尔伯特和波利亚猜想已在量子域理论中有重要应用.
麦凯(R.S.Mackay)在2017年指出,黎曼猜想的策略是证明ξ的零点对应于某个哈密顿算子的特征值,其原因为任意哈密顿算子的频谱是实的.这个策略归功于希尔伯特和波利亚[9].很奇怪,波利亚在他1926年的论文中没有提到谱策略,也没有使用谱策略证明相关问题.麦凯在该文中的目的是寻找一个哈密顿算子,其特征函数是(z),但此目标没有实现.他通过不同的方法得到波利亚使用的函数2ϑ(iw/2;π).
波利亚在“某类整函数的零点”(1918)和“具有实根的三角积分”(1927)中强调,他在三角积分零点实性的工作来自于黎曼函数可以用三角积分表示,进而可通过三角积分的研究探讨黎曼猜想.基雅科瓦(V.Kiryakova)“关于鲁塞夫的一些贡献”(2012)中指出,波利亚开创了由傅里叶变换定义的整函数零点分布问题研究的主题,并成为系统研究三角积分零点实性的最大贡献者.
3 波利亚的重要工作
波利亚在三角积分定义的整函数的零点实性方面的论文有 “某类整函数的零点”(1918),“某类超越整函数零点分布的几何学”(1920),“由傅里叶积分表示的整函数的零点”(1923),“某类三角积分的零点”(1926),“黎曼zeta函数积分表示的注释”(1926),“欧拉的超越方程的注记”(1926),“具有实根的三角积分”(1927),“延森的代数函数理论研究”(1927)等8篇文章.本文对这8篇文章进行深入解读,较为系统地揭示波利亚的重要思想和方法.

的零点分布,其中f(t)在[0,1]内是非负非递减函数.在该文前言中,波利亚给出了只有实根的的例子,其中J0(z),J1(z)为贝塞尔函数.波利亚在这些事实的激发下研究f(t)的性质,使U(z),V(z)只有实根.
为了形式化和证明相关定理,他在该文中引入实函数f(t)的类P[0,1),t∈[0,1].若f([0,1))是一个有限集,对这个集合的子集C,f−1(C)为[0,1)内以有理数为端点的子集,则称该函数f(t)∈P[0,1)为例外情况,否则为一般情况.关于U(z),V(z)的主要结果是:若f(t)∈P[0,1)为一般情况,则U(z),V(z)只有单重实根,且规律分布.若f(t)为例外情况,则U(z),V(z)只有实根,且有无穷多个是相同的,每个这样的根对V(z)是二重的,U(z)是单重的.若f(t)是递增的凸函数,则V(z)只有实根;若f(t)是递增的凸函数,右导数不属于例外情况,则U(z)在((2k−1)π/2,kπ),k∈N只有一个根,没有虚根.若f(t)是递减的凸函数,f′(t)为右导数,−f′(t)属于一般情况,则U(z)只有实根.f(t)是递增的凸函数,f(α)=0,α∈(0,1),若则U(z)只有实根.若则U(z)只有两个非实根.只有实根且有无穷多个相同根,比U(z),V(z)更大的函数类在鲁塞夫的1974年的文章中给出[10].卡萨多瓦(I.M.Kasandrova)在“只有实根的一类整函数的一些结果”(1977)中给出了保证这些相同根的充分条件为U(z),V(z)只有实根,且每个函数的两个相邻根的距离不大于π.一个类似问题在卡萨多瓦的“一类整函数零点的分布”(1984)中再次讨论[11].赛勒斯基(A.M.Sedletski)在2000年考虑了一般情况,删掉了他证明,若f(t)是正的非递减凸的非常值函数,则V(z)只有单重实根,0≤t≤1[12].基(H.Ki),金姆(Y.Kim)在“实整函数非实根数和傅里叶-波利亚猜想”(2000)中在假设f(t)∈P[0,1)的一般情况下,探讨U(z),V(z)的非实根情况.

则F只有实根,且在区间 ((2n−1)π/2σ,(2n+1)π/2σ)内只有一个根[13].
设f(t)在[a,b]内为连续正的实整函数,除有限个点外可导,
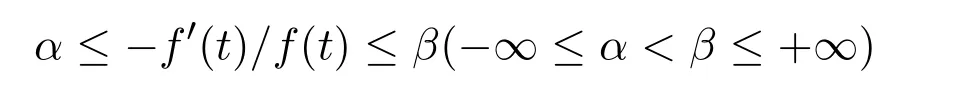
不恒为常数,波利亚证明

的所有零点都位于α

的零点总是位于−1 值得一提的是,格洛莫(J.Grommer)在希尔伯特指导下完成博士论文“具有实根的超越整函数”(1914).波利亚在该博士论文中发现了胡尔维兹关于只具有实根的整函数未出版的定理之一的一种改进,这在关于胡尔维兹的遗文评论中有详细介绍.胡尔维兹和波利亚一直在讨论这个问题,在胡尔维兹的日记中有“波利亚定理”的记载.在该日记中,记有关于拉盖尔(E.Laguerre)定理的注记及贝赫尔(C.Biehler)关于整函数实根的定理应用与评论.在1914年2月26日,波利亚发表了与之有关的一篇文章“整函数的一个问题”.贝赫尔在“全部实根的代数方程类”(1880)中涉及该问题.胡尔维兹在该日记中提到“贝赫尔定理漂亮的应用昨晚进入我的脑海”. 在该文第六部分“零点的区分”中,波利亚探讨 的零点分布问题,其中α≥−1.他得到,当α>1时,该函数无实根.当α=1时,该函数只有二重实根.当−1≤α<1时,该函数只有单重实根.该例后来在 “欧拉的超越方程的注记”(1926)中重新探讨.波利亚在该注记的注脚处指出,在前段时间讨论过Fα(z)的实根问题.现在所用方法有些不同.该例其实欧拉早先处理过 1−z2/α(α+1)+z4/α(α+1)(α+2)(α+3)−z6/α(α+1)(α+2)···(α+5)+···=0,其中α>0.波利亚指出,“他不知道欧拉的日记,该函数是在 1791年发表的一篇欧拉笔记的文章中提到,鲜为人知,但非常有意义,它是关于z的整函数的第一个例子,由Fα(z)表示.欧拉注意到α=1,2,3,4时的根的情况后,令人钦佩的断言道,当 0<α≤3时,Fα(z)只有实根;当α>3时,Fα(z)无实根.欧拉近似计算了α=1/2,1/3,1/4时的根.欧拉没有证明该断言.这是一个非常幸运的断言,该断言可以在不诉诸复杂运算和推理过程下完成”.波利亚用关于多项式的有关理论推导了该断言.在“只有实根的三角积分”(1927)中给出更一般结果. 在这篇文章里,另一有兴趣的注释是波利亚用维格特定理代替最小模定理确定了对于有限阶的整函数的阿达玛乘积表示.波利亚在“有限阶的超越整函数乘积的新证明”(1921)中以完全不同的方法证明了该定理. 在该文第七部分“收敛指数的确定”中,波利亚只假设f是可积时,处理了 的具有收敛指数1的零点列问题.当F(z)为指数可和时,类似情况在波利亚的“某类超越整函数零点分布的几何学”(1920)中讨论.这篇论文的目的是对指数多项式零点分布从几何角度研究,给出一般性定理,但没有证明.详细和进一步的结果出现在其学生施温格勒(E.Schwengeler)的博士论文中[14](1925).蒂奇马什(E.T.Titchmarsh)在“某类整函数的零点”(1926)中对此也有进一步的阐述.波利亚的这个工作开创了指数类型的整函数零点分布的现代理论.波利亚除在“第105个问题解的注释”(1933)及“整函数和多重傅里叶积分”(1937)中有所涉及外,他没有对这个主题做太多贡献.中国学者李文清在20世纪50年代末期也对此问题有深入研究. 在该文中,波利亚隐含地给出了给定一个函数为特征函数的充分条件:f是在R上的实值连续函数,f(0)=1,f(t)=f(−t),f是凸的,对于该结果被波利亚在“函数方程的高斯误差定理分析”(1923)中使用.他在1949年加州大学伯克利分校学术会议上宣读的论文“特征函数的注释”中再次阐述并给出一些有意义的例子. 波利亚在1918年的论文中指出这种通过研究傅里叶变换零点实性的方法不能顺利得到黎曼猜想的完整证明.蒙哥马利在1973年提出的“对相关猜想”支持了波利亚的这一论断. 有无穷多个实根.当α=2时,Gα(z)对于实变量值恒正.据此,他猜测 也如此,但事实相反.他的想法受到龙格和波利亚关于积分方程实可积性问题的影响.波利亚在“关于龙格处理的积分方程”(1914)中曾论及. 波利亚在“由傅里叶积分表示的整函数的零点”(1923)中开头提到,“我们不具备一般方法讨论由傅里叶积分表示的整函数的零点的实性(这样的方法对黎曼zeta函数可以应用).我在这阐述一种特殊情况,在其中的讨论不仅琐碎,而且可在已知结果的帮助下进行”.波利亚考虑 的零点分布,α取正实值,证得以下结果:若α=2,则Gα(z)无根.若α=4,6,···,则Gα(z)有无穷多个实根,无复根.若α>1不是偶整数,则Gα(z)有无穷多个复根,实根数不超过 2[α/2].这个结果的一般化由布鲁因 (de Bruijn)在 1950年给出[16].卡米牟特(J.Kamimoto)在1998年证明该函数除了有限个零点外都是单重的,并猜想α=4,6,···时,该函数的所有零点都是单重的.卡米牟特,基,金姆在 1999年把该猜想一般化,证明这个函数及其各阶导数的零点都是单重的[17].哈勒姆(M.Hallum)在2014年排除了α<1的情况,对波利亚的结果给出了详细证明,方法略有不同[18]. 柯西在 1853年,莱维在 1923年证明Gα(z)≥0,0<α≤2,x∈R.伯韦尔 (R.Burwell)在 “广义超几何函数的渐近展开”(1924)中对α=3,4,5,···讨论了Gα(z)的渐近展开,证明α=4,6,···时,Gα(z)的复根数是有限的. 波利亚的 “某个三角积分的零点”(1926)专攻黎曼猜想,由下面的评论开始,“函数F(u)具有何种性质才能充分保证积分 则G(z)为黎曼ξ(z)函数”.“我已经发现了一些准则回答提出的问题,但在这不能给出,因为他们相当不系统,且有试探性的特征.我举一些例子,证明G(z)为具有实根的整函数”.波利亚给出整函数G(z)只有实根的一些具体情况. (1)F(u)=(1−u2n)α−1,0≤u<1,α>0,F(u)=0,1≤u<∞; (2)F(u)=exp(−u2n−αu4n)α−1,α>0; (3)F(u)=exp(−2αcoshu),α>0; (4)F(u)=8π2exp(−cosh(2u))cosh(9u/2); (5)F(u)=(8π2cosh(9u/2)−12πcosh(5u/2))exp(−2πcosh(2u)). 这5种情况的傅里叶变换的零点实性在该文中未证明.波利亚利用哈代的方法得到下面简单的准则:对于实值u,设F(u)是一个偶的解析实值函数,且有 若G(z)只有有限多个实根,则存在一个整数N,使得 |F(n)(it)|是t的增函数,若n>N,0 情况(1)是贝塞尔函数Jα−1/2(z),其零点都是实的,在 1918年论文中出现,一般形式为“只有实根的三角积分”(1927)定理II的例子,情况(2)为“只有实根的三角积分”(1927)中定理 I的例子,情况 (3)在 “黎曼 zeta函数积分表示的注释”(1926)中证明,在 “只有实根的三角积分”(1927)中再次证明.蒂奇马什在 “黎曼 zeta函数理论”(1951)中详细讨论了情况(4)和(5).在讨论(4)时,在指数处漏掉2π. 在“黎曼Zeta函数表示的注释”(1926)中,波利亚讨论了余弦变换零点的分布问题.兰道在 1913年与他的一次交谈中提到当 Φ(u)由 4π2exp(9u/2−πexp(2u))代替时,是否只有实根.这导致波利亚定义 证明它只有纯虚根.通过ξ∗(z)=2π2ϑ(iz/2−9/4;π)+ϑ(iz/2+9/4;π),证明ξ∗(z) 只有实根.比恩(P.Biane)在2009年主要考虑ϑ(iz/2;π)为ξ的另一种近似.他定义函数 麦克唐纳函数零点的谱解释在当时已众所周知,但波利亚没有提到.波利亚利用 (2µ/x)Kµ(x)=Kµ+1(x)−Kµ−1(x)以非常聪明的方法证明ϑ(z;x)的零点为纯虚根,而比恩利用Kiµ(x)的积分表示及固定相位法得到同样的结果.卡茨(M.Kac)在评论波利亚的这篇文章时指出ξ∗(z)的结果可以通过伊辛模型中的李-杨定理推导得到.卡茨评论到:“尽管这篇美丽的文章把人带到了与黎曼猜想极短的距离,但它似乎不能激发出更多进一步工作,且在后来数学文献中参考它的是相当缺少的”.比恩在该文中指出“由波利亚考虑的函数以一种非常巧妙的方式与黎曼ξ函数有关,而不是一眼见到它立即就能体现出来的,进一步讲,这种关系的本质是概率的,应以这种观点看待波利亚的论文”. 布鲁因深受波利亚的影响,在1950年的论文中使用一个非标准积分表示 只有实根.他也给出第二个近似 证明该变换只有实根.Ξ(2z)的积分形式后来在索达斯 (G.Csordas),诺米柯 (S.Norfolk),瓦尔加(S.Varga)的“对于布鲁因-纽曼常数Λ的下界”(1988)中使用.海哈尔(D.Hejhal)在1990年证明,当 加斯珀(G.Gasper)在1994年“利用平方和证明某类整函数只有实根”论文的基础上,在2008年给出利用某个实值特殊函数的平方的积分给出ξ∗(z),Kiz(a),Fa,c(z)等函数零点实性的新证明,并用于证明海哈尔的有关结果[22].波利亚在“只有实根的三角积分”中指出G(z)=K1/2iz(a),并证得 只有实根.史把ξ∗表示为 4π2(K(iw/2)+9/4(2π)+K(iw/2)−9/4(2π)).孔泰 (A.Comtet)在1993年进行研究,麦凯在1997年曾暗示贝里(M.Berry).以此为据,贝里和基廷(P.Keating)在 “黎曼零点和特征值近似”(1999)中用谱方法证明黎曼猜想,得到较好结果[23]. 在该文中还包括下面的命题:a>0,G(z)为0类或1类整函数,对于实值z取实值,没有虚根,且至少有一个实根,则G(z−ia)+G(z+ia)只有实根.波利亚用该命题研究函数ξ∗(z),证明ξ∗(z)和ξ(z)在临界线上有相同的零点数.他在文末注脚处指出对于最佳估计 (2π2cosh(9u/2)−3πcosh(5u/2))exp(−2πcosh 2u)可有同样的结果.布鲁因已把该定理以不同的方式一般化,不同于后来的卡登(A.Cardon).卡登在2000年推广为 ∑G(±ia1±ia2±···±ian)exp(±ib1±ib2±···±ibn),其中ai>0,bi为实数. (1)F(−t)=F∗(t),∗表示共轭运算; (2)F(t)是局部可积的; (3)存在正常数A和α,当 |t|充分大时,|F(t)|≤Aexp(−|t|2+α).波利亚讨论了F(t)在何条件下只具实根.为了形式化和证明他的结果,他引入了保证根的实性的广义因子概念.φ(t)为广义因子,若对任意具有实根的整函数 也只有实根.他证明实解析函数φ(t)是一个广义因子,当且仅当在C内φ(iz)为第二类整函数.他推导出一个傅里叶变换的零点和广义因子定理,利用“波利亚-舒尔函数”把先前有关论文的结论一般化. 设实函数f(t)是绝对局部可积的,且存在正常数B,β,使得 假设f(t)在原点的邻域内可解析开拓,波利亚证明复函数 只有实根.若P(z)为只有负根的实代数多项式,l,q为正整数,则 也只有实根.令P(t)=(1+t)k+l−1,波利亚得到 也只有实根.鲁塞夫在“一类整函数零点的分布”(1961)中把 的零点分布推广到黎曼-斯特灵积分意义下的整函数的零点分布.设f(t)和Ψ(t)是实函数使得是递增凸函数,则 只有实根,其中0≤t≤1. 布里奥因(L.Brillouin)在1916年,伯韦尔在1924年利用渐近展开法研究 的零点分布,更为准确的结果由塞努夫(D.Senouf)在1996年得到[24].波利亚在1927年研究了 则φ1(z)无根.对于n≥2,φn(z)有无穷多个实根.巴霍姆(N.G.Bakhoom)在1935年有论及[25].这些结果的一般化由布鲁因在1950年得到,卡米牟特,基,金姆在“拉盖尔-波利亚函数零点的重数”(1999),卡登在“只具实根的傅里叶变换”(2004),基,金姆在“傅里叶积分的零点分布和近似行为”(2007)中有进一步的研究.帕里斯(B.Paris)在“关于一类傅里叶积分的近似性和零点”(2012)中通过使用莱特函数的近似理论得到它们的渐近展开,并考虑这些积分的实根和复根情况.这一方法不同于前人使用最速降线法.这些结果后被推广到类似结构的p维傅里叶积分. 胡斯诺夫(H.Huseynov)在2009年证明了一个定理使得波利亚论文中的函数F(λ)只有实根,其中 这些结果波利亚通过使用拉盖尔定理得到,而胡斯诺夫利用自己证明的定理完成[26]. 很可能受对胡尔维兹遗稿研究的激励,波利亚研究延森的遗文,使他完成一篇关于黎曼Zeta函数积分表示的全面考察的论文“延森的代数函数理论研究”(1927).文章主要部分是“某个三角积分零点的实性”,在其中讨论exp(−λz2)H(z)的零点问题,其中函数H(z)的阶小于2,λ为非负实数.他特别研究 情况,Ψ(t)满足下面性质: (1)Ψ(t)是不恒等于0的非负实函数; (2)Ψ(t)任意阶可导; (4)F(z)的阶小于2. 黎曼ξ函数为该函数特例.波利亚指出当t→±∞时,Φ(t)近似于 波利亚在延森遗稿中发现一些关于F(z)零点分布的结果,并形式化. (1)若 Ψ′(t)≤0,t≥0,则F(z)没有实根; (2)若F(z)在−k≤Im(z)≤k内有无穷多个根(k>0),则 (3)若F(z)只有实根,且F(z)=b0−b1z2/1!+b2z4/2!+···,则b0,b1,b2,···符号相同. 波利亚指出F(z)零点实性的必要条件为该族不等式构成了黎曼猜想正确性的必要条件,因为任何一个失败,则该猜想都不能证明.关于这个问题的第一个进步由格劳斯瓦尔德(E.Grosswald)在1966年迈出.索达斯,诺夫柯,瓦尔加在“黎曼假设和图兰不等式”(1986)中继续研究,把直接计算转化为核Φ(t)的矩不等式,对充分大的n进行证明.索达斯和瓦尔加在1988年对更一般核进行研究.遗憾的是,该不等式对黎曼ξ函数不满足. 波利亚在该文中研究了F(z)不具有形式 exp(αz)P(z)的情况,其中α为常数,P(z)为代数多项式.令 则F(z)只有实根当且仅当x为实数,n=1,2,···.波利亚探讨 当0 伯尔(H.Bohr),兰道在1914年证明ζ(s)的大部分复根位于1/2−δ<σ<1/2+δ,δ>0.受他们影响,哈代在1914年证明在ζ(s)的零点中,有无穷多个位于直线σ=1/2.兰道在 1915年曾评价道:“对于数学最大的进步最近一段时间属于哈代关于黎曼ζ(s)零点的注记”.在胡尔维兹的数学遗稿中可以找到哈代证明的梗概.波利亚在该文中利用上述判断准则改进了哈代的证明.兰道在“数论讲义”(1927)中也给出一个简单证明.哈代证明较简略,查迫灵(R.Chapling)在“哈代定理的哈代证明”(2014)中增补了哈代证明的细节.桑格尔(U.K.Sangale)在“关于哈代定理的注记”(2016)中给出哈代关于黎曼ζ(s)的简单证明. 受波利亚 1918年和 1920年相关工作的影响,蒂奇马什在 “某类整函数的零点”(1926)中研究 的零点分布,其中f(t)为实可积函数,或f(t)=f1(t)+if2(t),f1(t),f2(t)在相同区间内是实可积函数.他把∫化为 的形式进行研究,并探讨当f(t)满足由波利亚1918年论文中的条件时,F(z)的零点分布情况. 谢卡洛夫(L.Tschakalo ff)受波利亚工作影响,在1927年致力于研究这样一类整函数,记为类(A),其零点在上半平面内的代数多项式或这类多项式的极限构成的函数,主要结果可看作是埃尔米特-比勒定理的推广.他证明 有无穷多个单重实根,α∈R,σ≥1/2.设f(t)是在(-1,1)内非负非递减的有界实函数,若α是实数,则 有无穷多个实根.若f(t)是波利亚意义下的一般情况,则Hα(z)的全部根是单重的;当α−β不是π的倍数时,则Hα(z)的每两个相邻根之间存在唯一Hβ(z)的根.在此基础上,他证得 只有实根. 设f(t)是在[−1,1]内有连续导数的实函数,若 至少有一个不等于0,则Hα(z)有无穷多个实根,有有限多个非实根.Hα(z)有有限多个重根,且相邻的实根之差在无穷处收敛于π[27].谢卡洛夫在1949年讨论在p(z)是有任意复系数代数多项式情况下, 的非实根数问题,特别指出,若p(z)是一个m次的实多项式,则至多有m个非实根[28]. 受波利亚工作影响,奥布雷克夫 (N.Obrechko ff)在1941年得到奥布雷克夫h-定理[29].设f(t)在 (0,1)内是正的非递减函数,实多项式h(z)的零点位于半平面 Rz≤1/2内,则只有实根.奥布雷克夫通过代数多项式零点结果获得只有实根,其中λ>0,R(z)为只有实根的多项式,φ(t)和ψ(t)在 (0,λ)内是非负函数,φ(t)是非增的,ψ(t)是非减的,φ(0)≤ψ(0),f(t)=φ(t)+ψ(t),0≤t≤λ,f(t)=f(−t),−λ≤t≤0. 在研究具有相应积分表示的复多项式类零点分布中代数传统出现于博约罗夫 (E.Bojoro ff)的 1949年论文中[30].令实函数f(t)和φ(t)满足条件f(t)>0,φ(t)>0,t∈(0,a),a>0;f(t)是递增的,φ(t)是递减的,定义 只有实根.迪米夫在1960年推广了博约罗夫的结果[31].令R(z)为具有实根的多项式,则 只有实根.若 |λ|≤1,则 只有实根. 伊利夫(L.Ilie ff)在“某类多项式和整函数的零点”(1940)中给出一个波利亚关于 的零点实性的初等证明.他证得 等只有实根,推广了波利亚的结果.在“一类整函数零点的分布”(1948)中,伊利夫给出了产生一类整函数类的方法,该整函数定义为只具实根的有限的余弦变换.这篇文章中的结果在“只具实根的整函数”[32](1949)中发表.令函数ψ(t)在(0,1)内正可积, 在(0,1)内非负增加可积, 在1955年,伊利夫对整傅里叶变换零点分布进一步研究,得到更为一般的结果[33].令p(z)为实偶多项式,或实偶整函数使 (1)p(a)=0,a>0;(2)p′(iz)在类 LP中.A(a)表示满足条件(1)和条件(2)的实偶函数p(z)的集合,z∈C.若p(z)∈A(a),p(0)>0,λ>−1,则只有实根.波利亚的只有实根,是实偶函数 1−z2q在 A(1)中的结果,q为正整数,λ>−1.若p′(iz)只有实根,正整数n>p(0),则存在一个唯一的正实数列an,使则只有实根,n充分大.令f(z)为非常值实偶函数,使f′(iz)在类LP中,若f(t)≥0,t∈(0,∞),则只有实根,推广了波利亚的有关结果.雷尼(A.Rényi)在1950年推广了伊利夫的研究结果.令n和m表示非负整数,实函数f(t)∈Cn(0,1),满足条件: (1)f(k)(1)=0,k=1,2,3,···,n−1; (2)g(t)=t−mf(n)(t)是(0,1)内非负非递减的可积函数; (3)若n+m为奇数,f(2k+1)(0)=0,1≤2k+1 只有实根.若n+m为偶数,f(2k)(0)=0,2≤2k 只有实根.设p(x)为非常值实代数多项式,0作为p(x)根的重数为k,1的重数为q.若k≤q,则存在正数a0使得只有实根.若k>q,对每个a,上述函数不只有实根.托多里诺夫(S.Todorinov)在1957年基于埃尔米特-比勒定理证得[34]. 布鲁因通过利用转移因子代替微分因子法,利用余弦变换建立了一个多项式导数非实根分布的延森定理的一个类似定理.当由更一般的超越整函数代替余弦函数时,是否有类似定理.这个问题在格雷文(T.Graven),索达斯在1994年提出,但未解决.该问题其实在阿蒂亚(M.F.Atiyah),博特(R.Bott),嘉定(L.Garding)“具有常系数的双曲微分算子的缺项Ι”(1970)中已见端倪.之后,格雷文,索达斯,史密斯(W.Smith)在“整函数的导数的零点和波利亚-威曼猜想”(1987)中也有所论及. 在该文中,布鲁因提出如下问题:设F(t)为一个定义在实轴上的复值可积函数,F(t)=O(exp(−|t|b))(|t|→∞),对某常数b>2,F(−t)=F∗(t),ε>0,除有限个F(t)的傅里叶变换零点外都位于Im(z)≤ε内.在这些假设下,对λ>0,exp(λt2)F(t)的傅里叶变换是否只有有限个复根.基,金姆在2003年对该问题给出肯定回答[35]. 波利亚第一个考虑了在 [0,1]上实黎曼可积函数的傅里叶变换零点实性与多项式零点分布之关系.借此他成功证明U(z),V(z)只有实根.在 “一类整函数零点分布”(1961)中,鲁塞夫研究了多项式零点的渐近性和U(z),V(z)零点分布之关系,推广伊利夫定理,其结果在 K.Do˘cev 1962的文章中得到加强[36].Do˘cev引入函数类Lα(λ),α,λ>0,即在[0,1]上复值黎曼可积函数f(t)具有性质,对任意δ>0,当n充分大时,多项式∑f(k/n)zk,n=1,2,3,···的全部零点位于圆|z|<1+(λ+δ)n−α内.若f(t)∈L1(λ),则的零点位于Im(z)≥−λ内.若f(t)∈L(λ),α>1,则的零点位于 Im(z)≥0内.卡萨多瓦在“一类指数类型的整函数零点分布”(1975)中指出,若令f(t)在[0,1]上是实勒贝格可积函数,若 则U(z)的零点位于平行于实轴的线条上;若 则V(z)的零点位于平行于实轴的线条上.他在1976年进一步完善Do˘cev有关结果.当α=1时,研究的零点分布情况. 鲁塞夫在1973年通过运用博约罗夫在1955年的论文中引入的函数类F及伯恩斯坦多项式理论证明 只有实根,其中F(t)∈B∩F,F(1)0是有界的实函数,f(t)∈ε是实黎曼可积函数.B表示由 的函数F(t)构成的集合,F表示由 一个给定的代数多项式的零点在单位圆内的算法出现在舒尔“只具负实根的代数方程”(1921)中,并在科斯托瓦 (M.Kostova)“类ε函数 II”(1973)和 “舒尔定理的应用”(1973)中应用.他在 “类ε函数 II”中指出,若f(t)∈ε,则只有实根.在“舒尔定理的应用”中,他提供了给定一个类ε函数产生同类函数序列的方法. 确定一个傅里叶变换是否只有实根的起源问题,除数论中的黎曼猜想外,另一个与数学物理中的李-杨定理和量子域理论有关.纽曼作为数学物理方面的专家较早涉及该问题.他在1976年引入他指出,若b≤−1/8,则b(z)只有实根[38].这些结果来自于某些量子域理论问题研究,但出于教学方法考虑,以黎曼猜想背景呈现.受其影响,舒马赫(D.Schumayer),胡尔钦森 (D.A.W.Hulchinson)在2011年也从物理角度论述此问题.在该文中出现了现今称为的布鲁金-纽曼常数.该常数由索达斯,诺夫柯,瓦尔加在1988年引入.黎曼假设等于说该常数小于等于0.奥德林克(A.M.Odlyzko),基等进一步加强纽曼结果. 波利亚,斯泽古在 “分析学中的问题和定理”(1978)中指出若f(t)在 [0,1]上为正的可积递增函数,则的零点为实的.沃克在 “某些三角积分的零点”(1988)中指出,当弱化可积性条件时,结论仍有效,如的根为实的,b>0,0 索达斯,瓦尔加在1990年研究 的零点,Φ(t)为雅可比theta函数.当0 卡登在“卷积运算和整函数零点”(2000)中令G(z)是阶小于2的具有实根的实整函数,存在分布函数F(z)使卷积 只有实根.他在 “卷积运算和整函数的零点”(2002),“卷积运算和具有单重零点的整函数”(2002)等文章中把某些分布函数µ(t)进行分类,使只有实根.他在 “只有实根的指数函数的和”(2004)中运用波利亚的辅助定理和证明过程,得到只有实根.他在 2005年特征化某些µ(t),使傅里叶变换只有实根[42].卡登的工作得益于皮利斯(I.Pinelis)在1994年论证的概率问题.亚当斯(R.Adams),卡登在2007年证明埃尔米特-比勒类整函数的乘积和只有实根,推广了卡登结果[43].应用这些结果构造只有实根的指数函数和的函数. 赛勒斯基(A.M.Sedletskii)在2009年在波利亚1918年论文及其2000年论文的基础上,在附加条件不是很大,且f(+0)>0下,讨论了U(z),V(z)小数目零点分布.对米塔格-莱弗勒函数的小数目零点分布也进行了讨论. 索达斯在“正定核的傅里叶变换和黎曼ξ函数”(2014)中开篇指出,直到现在也无已知的充要条件使一个好的核K(t)满足傅里叶变换只有实根.索达斯在该文中考察整函数可表示为某些可接受核的傅里叶变换的零点分布,主要结果揭示正定核的博赫纳-卡欣奇-马赛厄斯理论和广义实拉盖尔不等式之间的紧密联系,雅可比theta函数的凹凸性在整个工作中起着重要作用. 在最近的研究中,寇百雅士 (H.Kobayashi)在 “与黎曼ζ(s)函数关联的ξ(s)和(t)的结果”(2016)中,采用对核S(t)进行分解的方法研究的零点分布.波尔森(G.Polson)更是提出了利用整函数的阿达玛因子法,研究核Φ(t)满足何种性质以充分保证傅里叶变换只有实根的问题[44]. 使某一函数K(t)的傅里叶变换是一个只有实根的整函数问题是一个未决问题.索达斯,杨在“有限傅里叶变换和黎曼ξ函数的零点”(2005)中指出“无已知的充要条件使一个好的核K(t)的傅里叶变换只有实根.正是这个基本问题激发了处理实整函数由傅里叶变换表示的零点分布的一些结果和问题”. 波利亚和许多其他的数学家都做了一些重要的工作,并提供了关于傅里叶变换的零点分布有兴趣和挑战性问题,使得这个主题不断创新且有各种现代成果出版.波利亚是系统研究三角积分零点实性的最大贡献者,他不仅提出了广义因子法和近似方法,奠定了其后三角积分零点实性研究的基础,而且其思想和方法一直影响到现在,其工作成为当今三角积分零点介绍和研究不可忽视的内容.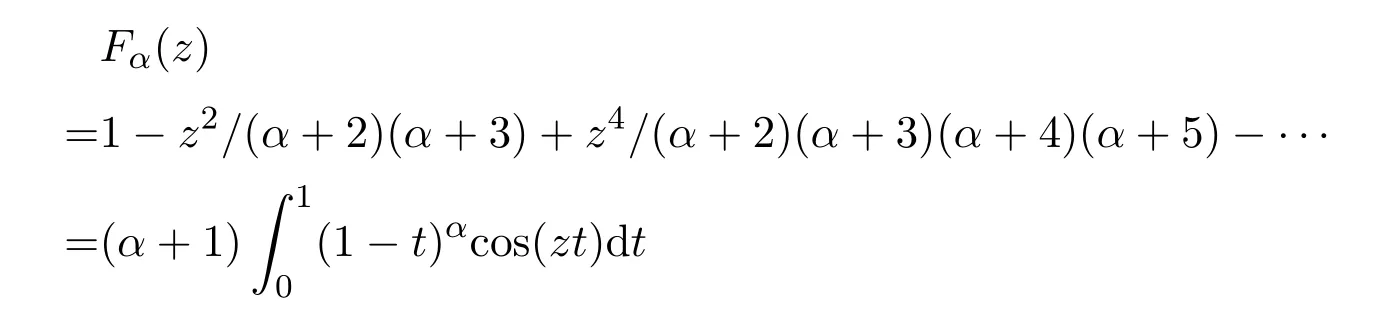





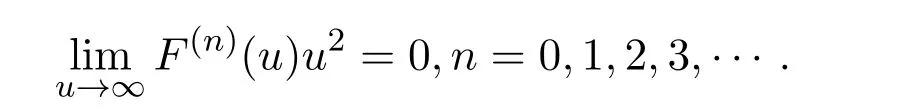

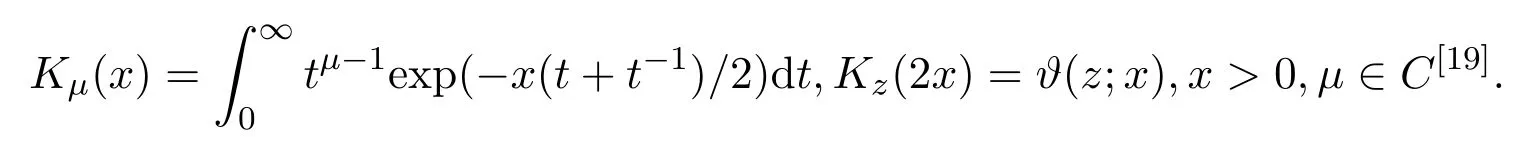
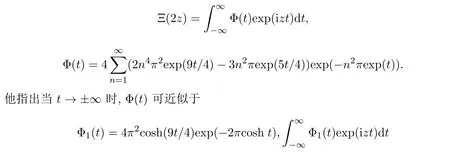



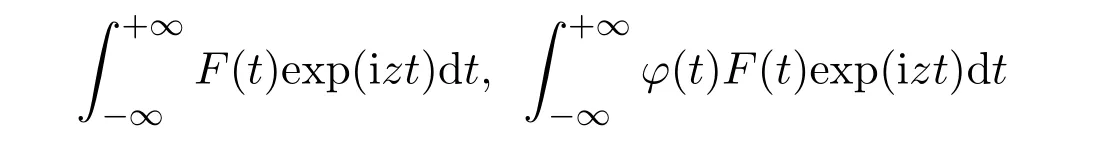
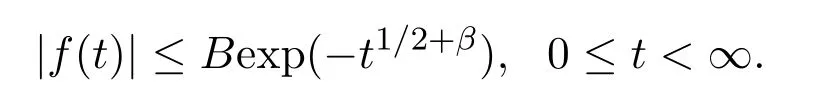


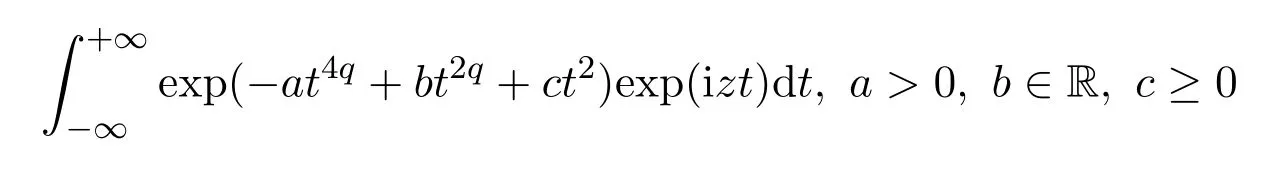





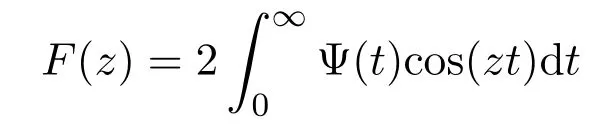

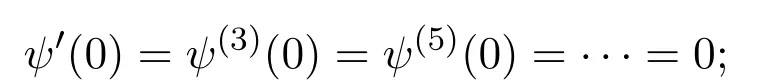
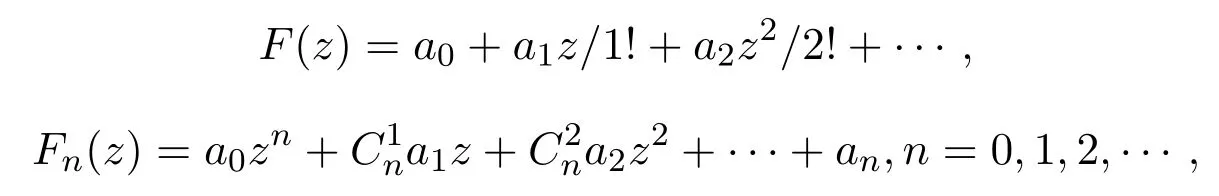

4 波利亚思想的影响

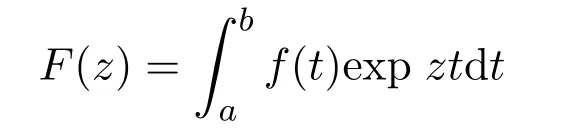

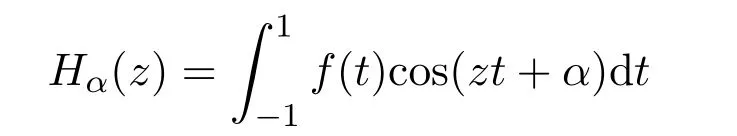










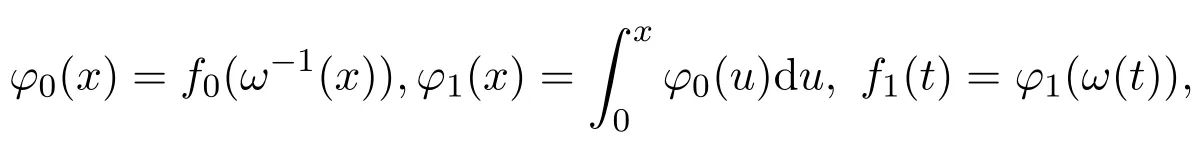







5 结语

