圆环上涉及重值及亏量的亚纯函数的唯一性
2019-12-26 09:51:36谭洋
纯粹数学与应用数学 2019年4期
谭洋
(北京师范大学珠海分校应用数学学院,广东 珠海 519085)
1 引言
假设读者熟悉亚纯函数的Nevanlinna值分布理论[1-2].亚纯函数的唯一性问题是值分布论中的一个重要研究课题,平面上亚纯函数的唯一性问题已经取得了丰硕的研究成果[3-5].文献[6-7]将亚纯函数的值分布理论推广到多连通区域――圆环.之后有学者研究了圆环上的亚纯函数唯一性问题[8].本文主要研究了圆环上重值及亏量对亚纯函数及其导数唯一性的影响,所得结果丰富了圆环上亚纯函数的唯一性理论.
本文采用圆环上亚纯函数Nevanlinna理论的符号[6-7].设f(z)与g(z)为两个非常数亚纯函数,k为正整数,a为任意复数,如果f(z)−a与g(z)−a在计重数(不计重数)之下具有相同的零点,则称a为f(z)与g(z)的CM(IM)公共值.Ek(a,f)表示f(z)−a的所有k重零点的集合(计算重数).Ek)(a,f)表示f(z)−a的≤k重零点的集合(计算重数);E(k(a,f)表示f(z)−a的>k重零点的集合.Ek(a,f)=Ek(a,g)表示f(z)−a的k重零点当且仅当是g(z)−a的k重零点.


2 几个引理





3 主要定理及证明
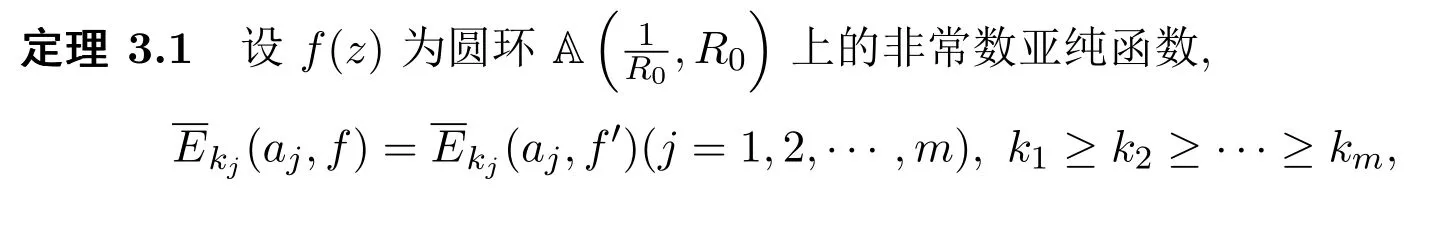







猜你喜欢
北京建筑大学学报(2022年1期)2022-03-29 03:16:30
大学数学(2022年1期)2022-03-21 12:59:52
北京建筑大学学报(2021年1期)2021-03-31 02:36:20
数学年刊A辑(中文版)(2019年2期)2019-05-20 09:53:08
数学物理学报(2019年1期)2019-03-21 05:26:12
数学年刊A辑(中文版)(2018年4期)2019-01-08 02:00:12
领导文萃(2015年13期)2015-08-03 03:14:56
油气地质与采收率(2014年5期)2014-11-28 05:35:38
数学年刊A辑(中文版)(2014年6期)2014-10-30 01:41:22
数学年刊A辑(中文版)(2014年2期)2014-10-30 01:40:58

