“再发现”是突破教学难点的有效策略①
——《数学归纳法》的课堂实录与思考

2019-12-26 07:15陶兆龙

数学通报 2019年11期

陶兆龙

(江苏省南京市金陵中学 210005)

突破教学难点一直是教师关注的问题.在长期的教学实践中，广大教师总结了很多突破教学难点的方法与措施.这些措施与方法，对于数学知识的学习与理解，确实发挥了良好的作用.但随着课改的深入，教学理念的更新，我们已经愈来愈清晰地认识到：数学学习不仅仅是为了获得数学知识与技能，更为重要的是如何提升学生的数学学科核心素养.在核心素养的背景下，突破教学难点，更应关注学生的数学思维过程.因而，“再发现”是突破教学难点的有效策略.本文结合《数学归纳法》的教学实践，谈谈如何通过“再发现”来突破教学难点的探索与思考.

1 内容分析

数学归纳法是以数学归纳法原理为根据的演绎推理,它将一个无穷推理过程转化为一个有限步骤的演绎过程,是证明有关自然数问题的有力工具.

苏教版2-2将数学归纳法安排在推理与证明这一单元,排在合情推理,数学证明之后,这样的编排既有利于数学归纳法的教学,也有利于合情推理与数学证明的教学.

推理与证明这一单元的学习可以较为系统地让学生掌握推理(合情推理与演绎推理)与数学证明的基本方法,对提高学生的逻辑推理能力,培养其数学核心素养有一定的促进作用.这也是本单元教学要达成的重要教学目标.数学归纳法作为本单元的收官之作理应承担这方面的任务.

数学归纳法教学存在的问题主要有:

(1)数学归纳法的引入过程简单化,只是强化数学归纳法的解题应用,导致不少学生不能理解数学归纳法原理,尤其是对递推步不知何意,解题时只会生搬硬套两个步骤.

较为常见的是通过多米诺骨牌的演示直接引入数学归纳法, 实际上即使经过讨论学生也很难将多米诺骨牌与数学归纳法建立起联系,难以促进学生的理解.

(2)缺乏整体考虑,在进行数学归纳法教学时不关注合情推理.欧拉说过,类比是伟大的引路人，类比和归纳是数学发现的重要工具.在学习了合情推理,数学证明后,如果不联系这些内容学习数学归纳法,学生不仅难以形成合理的知识结构，也错过了运用类比与归纳进行“再发现”学习的最好时机.

(3)问题(含例题)的选择不能体现数学归纳法的优势,有很多问题不用数学归纳法解决更简单,强行应用数学归纳法反而使学生感受不到学习新知识的必要性,对数学归纳法的学习产生抵触情绪,思维活动无法展开.

由以上的分析可以看到,不论从单元教学,还是数学归纳法本身教学出发,数学归纳法的教学都应突出类比与归纳在数学“再发现”过程中的作用，强化逻辑推理这一核心数学素养的培养.

本节课的教学目标：了解数学归纳法原理，能用数学归纳法证明一些简单的命题，体会演绎推理将无穷归纳过程转化为一个有限步骤演绎过程的魅力,感受逻辑推理在数学发现和证明中的强大作用.

教学难点是“由n=k推证n=k+1”的递推过程.

2 课堂实录

2.1问题情境

师:提出问题: 求和 13+23+33+…+n3=?(记为P(n)=?)

引导学生采用归纳推理形成猜想,并注意利用P(2)算P(3),利用P(3)算P(4).

[教学意图:由P(2)算P(3)或者P(3)算P(4)一是简化计算,更重要的是为后面的递推作铺垫]

生:猜想:

师:上述猜想是否正确呢?怎样判断?

生:利用猜想再算几个看看!

……

师:回顾一下前面的讨论,实际上是这样的一个思路:

P(4)⟹P(5)⟹P(6)⟹P(7)⟹……

这样依次由前一个推出后一个,推算的再多也只是有限个,也不能保证猜想对所有正整数都成立.

既然由特殊不能推一般,那么应该怎样推证?

生:……一般化,由一般推一般!

师:你这里是利用

来推证

13+23+33+…+k3+(k+1)3

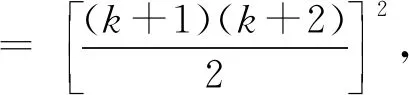
[教学意图:帮助学生理清思路,有不少学生还没弄清是怎么回事]

师:但是P(k)是不是正确,还没有证明啊?

生:假设它成立.

师:怎么敢假设它成立呢?

[教学意图:这里是一个疑点,关系到学生对数学归纳法的理解,要作停顿,逼学生交待清楚!]

生:P(k)是否为真可以先不看,只要看命题:P(k)⟹P(k+1)是否为真即可.

师:哦,上面的证明实际上是得到这样一个结论:假如P(k)为真,则P(k+1)也为真.那这样能保证上面的猜想成立吗?

生:可以,因为k可以取任意正整数,所以对任一个正整数n,有

P(1)⟹P(2)⟹P(3)⟹P(7)⟹P(8)…

⟹P(n)

师:这一招真好,一招制胜!

只要这一招就行了吗?

[教学意图:阐明数学归纳法的两个步骤的必要性]

生(讨论):没有P(1)成立不行,无法启动.

师: 两个步骤缺一不可!

观看多米诺骨牌视频(苹果手机广告片),让学生讨论怎样才能保证骨牌全部倒下?

最终得出结论:

(1)前一张倒下要能推倒后一张,(2)推倒第一张.

再与与前面的问题相比较,弄清其中蕴含的递推思想: “(1)前一张倒下要能推倒后一张”相当于“命题:P(k)⟹P(k+1)是否为真”,而“(2)推倒第一张”相当于P(1)成立.

[教学意图:先解决前面的问题,再演示多米诺骨牌视频,为前面较为抽象的方法提供一个直观的背景,通过对比,有利于学生进一步理解前面的方法]

师: 我们前面解决问题的方法就是以下的数学归纳法公理.

2.2数学理论

对于某些与正整数有关的数学命题，我们有数学归纳法公理：

(1)当n取第一个值n0(例如n0=1，2等)时结论正确；

(2)假设当n=k(k∈N*，且k≥n0)时结论正确，证明当n=k+1时结论也正确.

那么，命题对于从n0开始的所有正整数n都成立.

师: 有了上述公理,要解决与正整数有关的问题,可以采用数学归纳法,只要看其是否满足(1)(2)两步即可.

由上面的讨论可知,第(2)步实际上就是要证明一个结论:“P(k)⟹P(k+1)”,所以要先假设P(k)成立,再由此推证P(k+1)成立.

2.3数学应用

例1：用数学归纳法证明：

给出完整的证明过程.

[教学意图:让学生熟悉数学归纳法证明的流程,了解有关的书写规范]

最后指出:在用归纳推理得到猜想后,由数学归纳法进行了严格的证明,得到了我们需要的结论.归纳让我们得到猜想,用数学归纳法给出严格的证明,先猜后证,相得益彰.

例2：求和：12+22+32+…+n2=?

归纳推理受阻后,引导学生类比

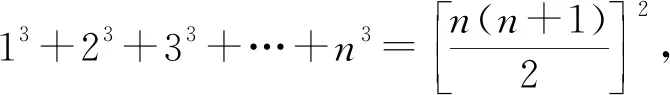
得出猜想: 结果应该是关于n的三次式,但系数不好猜!

师:猜的合理吧? 即

12+22+32+…+n2=an3+bn2+cn+d.

现在的问题是:a,b,c,d能否想办法求出来?

生:特殊化,n取4个特殊值1,2,3,4,可以求出a,b,c,d.

师:现在我们得到

这个结果还需要证明吗?

生:要！结果是猜出来的,要用数学归纳法证明.

师: (在让学生写出证明后)回顾一下,是怎么猜出来的?

生:类比和特殊化.

师:和例1采用归纳推理作出猜想不同,我们用类比的方法猜出右端应为关于n的三次式,再用特殊化的方法求出系数,最后用数学归纳法进行了论证.

合情推理可以帮助我们发现结论,得到猜想,数学归纳法使我们多了一种严格证明有关猜想成立的方法.有数学归纳法保驾护航,我们就可以大胆地进行有关猜想!

2.4课堂练习

设n为正整数,试比较2n与n2的大小.

最后指出

(1)n的初值n0不一定是1.

(2)仅由P(k)⟹P(k+1) 不能保证结论正确.

[教学意图：本题的结论较复杂,正确结论是

21>12; 22=22; 23<32; 24=42,当n≥5时,2n>n2.

但当k≥3时,

若2k>k2,则2k+1>2k2,

2k2-(k+1)2=k2-2k-1=k(k-2)-1,

上式大于0，所以2k+1>2k2>(k+1)2，

即可由P(k)⟹P(k+1),

但23<32, 24=42与2n>n2矛盾.这表明递推步不能保证命题成立.因此,本题可以进一步训练学生归纳猜想能力,加深对数学归纳法两个步骤缺一不可的认识]

2.5课堂小结

(1)讨论:用数学归纳法证明有关正整数问题的两个步骤及表达规范，强调递推步实际上是证明一个命题“P(k)⟹P(k+1)”成立.

(2)合情推理让我们体验到数学发现的乐趣,而数学归纳法又使我们感受到了演绎推理

的力量,这种感觉真好!

3 教学思考

普通高中数学课程目标要求通过高中数学课程的学习，学生能够获得进一步学习以及未来发展所必需的数学“四基”(包括基本思想、基本活动经验)，提高“四能”.在学习和应用数学的过程中发展数学学科核心素养.普通高中数学课程标准还提倡教师要善于根据不同的内容和学习任务采用不同的教学方式，优化教学，抓住关键的教学和学习环节，增强实效.

在日常教学中，教学难点几乎是师生每节课都要面临的问题，所以教学难点的破解策略直接关系到高中数学教育目标的落实.作为课堂教学关键环节教学难点的教学不能仅仅满足于使学生理解有关内容，还应承担发展学生数学核心素养的任务.

3.1“再发现”是突破教学难点的有效策略

怎样在突破教学难点的同时，学生的数学核心素养也得到一定的培育？

普通高中数学课程标准大力提倡教师注意引导学生独立思考、自主探索、合作交流.

荷兰著名数学教育家弗赖登塔尔认为，通过再创造(再发现)获得的知识与能力要比被动方式获得者，理解的更好，也更容易保持.

“再发现”是我们突破教学难点的必然选择.

“再发现”不是让学生完全经历数学家发现或发明数学的过程，而是基于学生的数学现实(原有的认知结构)，让学生在教师的引导下运用数学思维方法与数学思想方法，经历操作、实验、猜想、想象、类比、归纳、交流、概括、反思等有意义的数学活动，实现数学化.

引导学生运用“再发现”学习数学知识，实际上就是让学生主动地参与到新知识的产生过程中去,由于数学思维方法与数学思想方法的运用可以极大地提高发现和提出问题、分析和解决问题的效率，因此，“再发现”可以有效地突破教学难点，与此同时，数学思维方法与数学思想方法学习或应用促进了数学核心素养的发展.

在本节课的教学中，针对学生学习数学归纳法存在的困难，采用了“再发现”的教学策略，在教师的引导下,学生们通过自主探索、合作交流实际上“再发现”了数学归纳法,取得了较好的教学效果.

3.2“再发现”需要精心设计与有效引导

从上述教学过程看，“再发现”突破教学难点教学策略的有效实施，离不开教师的精心设计与有效引导，以下两个方面值得关注.

3.2.1 “再发现”需要好问题的驱动

数学归纳法引入或应用的教学中,如果选用一些简单的不用数学归纳法也能解决的问题(例题),那么学生就会对数学归纳法产生疑问：学习这一方法干吗?学生的思维会完全处于抑制状态.本节课中选择的三个问题,充分体现出数学归纳法的应用价值,还解决了困扰他们很久的问题:会猜想而不会证明.这样的选择,激发了学生学习数学归纳法的兴趣,激活了学生的思维.引入部分的问题对学生来说有一定的挑战性，通过合作交流得到猜想使他们得到了成功的体验，问题的解决最终带来了新知识的“再发现”.课堂上学生情绪饱满,讨论热烈,取得了很好的教学效果.

“再发现”需要好问题的驱动.突破教学难点时，教师首先要对新知识的形成、发展过程作出逻辑模拟，在此基础上设计好适合学生数学现实的问题，然后引导学生运用数学思维方法和数学思想方法分析问题、解决问题，从而发现新知识.

3.2 .2 “再发现”需要聚焦思维过程

教学难点的确定并非轻而易举的事.要突破突破教学难点，首先要准确地确定教学难点.

这就需要教师聚焦学生的思维过程，进行换位思考.精准地定位后才能有的放矢地去破解.

本节课的教学难点是“递推步”，学生对此感到难以理解：明明是要证明P(n)，却竟然假设P(k)成立！不是循环论证了吗？

所以在教学过程中,抓住机会，直面这一难点,反问提出设P(k)成立的同学,怎么可以这样做(假设P(k)成立!)？这个问题实际上是替学生问的,提出了他们的困惑!而问题解法的本质是要推证出一个真命题“P(k)⟹P(k+1)”,即:如果P(k)成立,那么P(k+1)也成立.

这样的处理使学生厘清了“递推步”的真实含义,对学生理解数学归纳法至关重要.

由学生提出“由一般到一般”的想法,老师再去质疑,是教学设计时最希望出现的场景,实际上就是希望学生能够“再发现”数学归纳法.为了达到这一目的,新课引入部分的问题设计及解决问题过程中的铺垫(P(2)⟹P(3)…)都起到了推波助澜的作用.

即使没有学生提出这样的思路,老师还可以进一步引导 “既然由特殊不能推一般,那么由什么可以推一般?” ,“P(k)⟹P(k+1)”是什么意思?怎么可以假设P(k)成立?等等。

充分的数学活动可以将学生的困惑，想法暴露无遗，再加上教师疑学生所疑,思学生所思,师生,生生之间就会产生思维碰撞,再发现就有可能产生，教学难点的突破就会水到渠成.

3.3“再发现”是发展数学核心素养的需要

从课堂教学的效果来看,在“再发现”的过程中合情推理与演绎推理的联袂使用起到了多米诺骨牌根本无法替代的作用!这种经历和感受对发展学生的逻辑推理素养意义重大，发展学生的数学核心素养离不开“再发现”，“再发现”不仅是突破教学难点的有效策略，也是发展学生数学学核心素养的需要.

课堂上有学生提出一般化的思路：“由一般推一般，即P(k)⟹P(k+1)”并非偶然.滴水穿石非一日之功,这是我们长期坚持不懈地运用“再发现”的策略进行有关训练的结果.

逻辑推理能力持续不断地训练提升了学生“再发现”的能力，能促使“再发现”的发生，而“再发现”的产生又进一步激发了学生学习合情推理的热情，两者相辅相成，相得益彰.