高考中关联数表的数列问题的研究与创新
刘胡良 宋宝和
(山东省教育招生考试院 250013)
数列是高中数学的重点知识之一,是刻画离散现象的重要数学模型,与高等数学中的极限、级数等内容联系紧密,是与高等数学衔接的重要内容,因此在高考中也是重点考查的内容.数列在高考中的考查形式多样,其中既有注重基础知识、基本技能“双基”的基础题目考查,也有突出“能力立意”,与其他知识相结合,注重考查能力和数学思想方法的难度比较大的题目.2017年高考数学中对于数列知识的考查,严格遵循了考试大纲的要求,基础性与创新性相结合,体现了育人与选拔相结合的命题理念.其中全国卷I理科数学中的一道数列题(第12题)是其中具有代表性的题目,题目创新性亮点突出,以基础知识为载体,注重考查数学思想方法与能力,实际上,历年高考中也不乏类似的经典数列考题,在此希望从这道经典考题入手进行深入探究.
1 一道经典试题
例1(2017理科数学全国卷I,12)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16 ,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )
A.440 B.330 C.220 D.110
从给出的数列前几项分析,所给数列不是简单的等比或等差数列,具有一定的规律性,题目中需要求解数列的前N项和,需要首先找出数列的排列规律.
由题意,不难发现该数列是等比数列20,21,22,23...部分的组合,可将该数列看成如下形式:
第一组:20,
第二组:20,21,
第三组:20,21,22,
……
第n组:20,21,22…2n-1,
每一组都是公比为2的等比数列,第n组的和为2n-1 ,则前n组的和Sn=21-1+22-1+…2n-1=21+22+…2n-n=2n+1-2-n.
不妨设所求的N在第n+1组第k个,则该项为2k-1, 1≤k≤n+1 ,
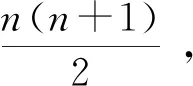
解法一因题目是选择题,不妨将所给选项代入SN验证,
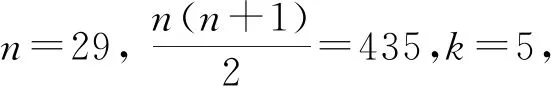
再验证比440更小的选项B、C、D是否满足前N项和为2的整数幂即可:
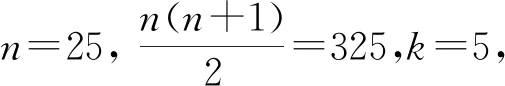
SN=226+25-25-3=226+4,不是2的整数幂;
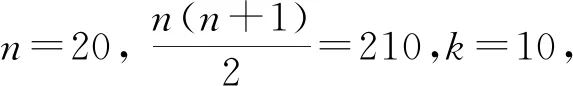
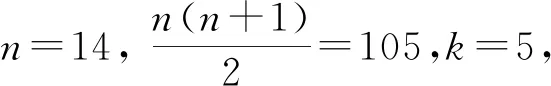
解法二要求解的N>100 ,所以n≥13 ,即N至少在第14组中,
SN=2n+1+2k-n-3<2n+1+2n+1=2n+2,
由n≥13可得 2n>n+3 ,
所以SN=2n+1+2k-n-3>2n+1+2k-2n>2n+1-2n=2n,
所以要使SN为2的整数幂,必有SN=2n+1;
因此2k-n-3=0,
当n=13时,k=4 ,则N=95<100 ,不满足题意;
令k=5,则n=29,N=440,即是所求的最小的N.
这道题目是选择题的最后一题,俗称选择题的“压轴题”,试题以日常生活中的软件激活码为背景,考查等比数列、等差数列相关知识,命制方式新颖,数列之中包含数列,跳出了数列通项公式的常用解题思路,对考生的创造性及对知识的灵活运用提出了更高的要求,但题中运用的等差数列、等比数列求和等知识点又是数列中最基本的内容,体现了基础性与创新性相结合的命题理念,重点考查转化与化归的数学思想方法,对考生的抽象概括能力、推理论证能力、运算求解能力和创新意识等都提出了更高层次的要求.
从解法中分析,发现数列按组排列的规律是解答的关键之一,将数列按组排列,即将原数列由“一维”变为“二维”形式,这种二维形式被称之为“数表”,所谓数表就是满足一定条件的数,按一定的规律排列成一个表,如著名的杨辉三角就是典型的数表问题.数表问题题型灵活、解法巧妙,在考查数列知识的基础上,对考生的数学思维及知识的灵活运用提出了更高的要求.数表问题在高考中并非首次出现,历年高考中多次出现利用数表考查数列知识的题目,下面通过几个比较有代表性的题目进一步探索这类数表问题的奥妙.
2 关联数表的数列典型试题
2.1 部分关联数表的数列高考试题解析
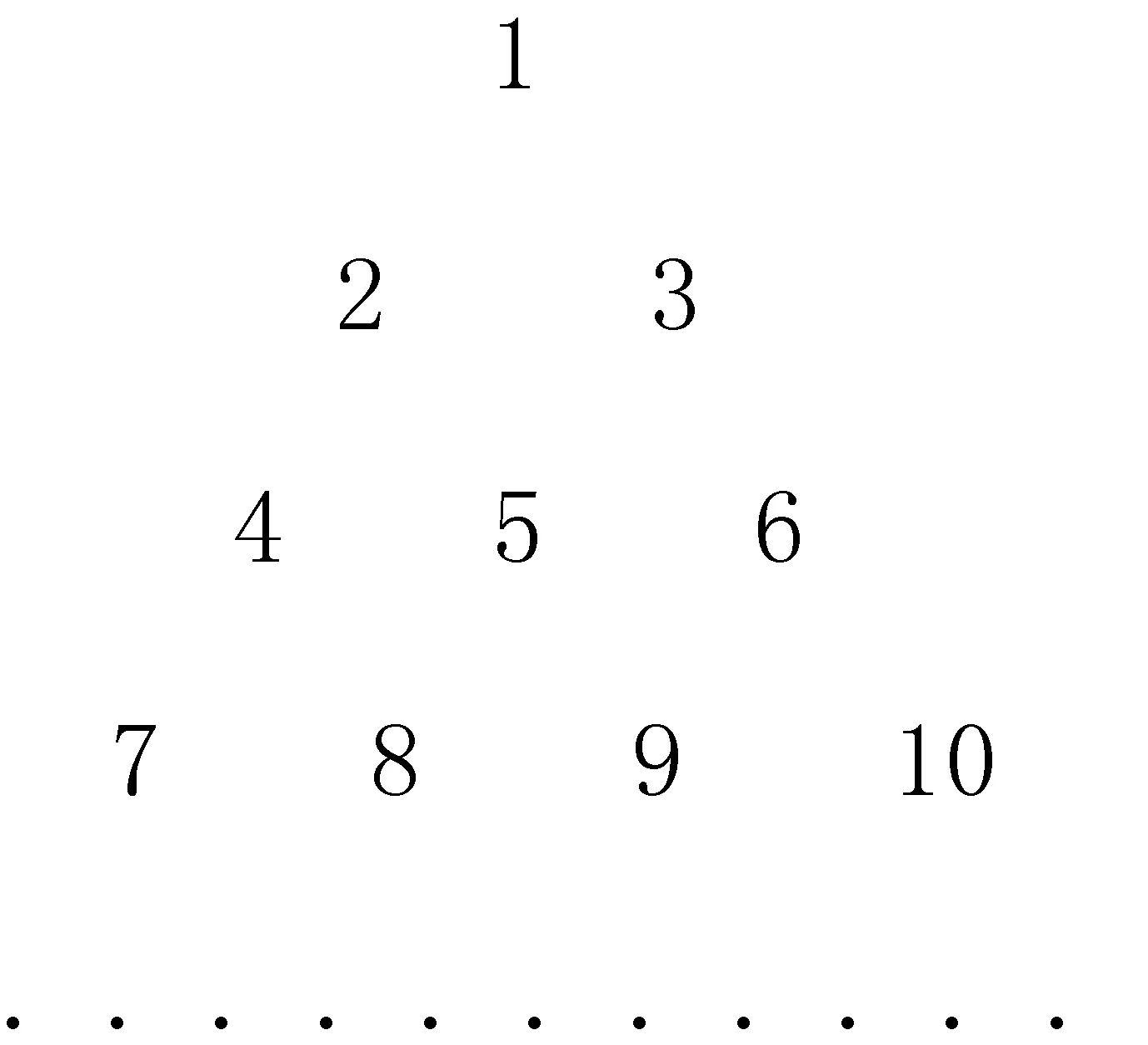
例2(2003年全国卷22)(Ⅰ)设{an} 是集合{2t+2s|0≤s a1=3,a2=5,a3=6,a4=9,a5=10,a6=12…, 将数列{an}各项按照上小下大、左小右大的原则写成三角形数表(如表1) 表1 (1)写出这个数表的第4、5行各数; (2)求a100. 解析数表中的每一项均是{2t+2s|0≤s 可发现数表中的第n行的数值满足2n+2s,0≤s 例3(2008年江苏卷10)将全体正整数排成一个三角形数表: 按照以上排列的规律,第n行从左向右的第3个数为________. 例4(2008年山东卷理科19)将数列{an} 中的所有项按每一行比上一行多一项的规则排成如下数表: a1 a2,a3 a4,a5,a6 …… 2017年高考试题中的例1与上述例2,例3,例4既有一定的联系,又存在一定差异.下面将从知识点、数学思想方法、数学能力考查等方面,对于这类关联数表的数列问题命题特点进行研究分析. (1)关于知识点的考查.上述数表问题考查的实质是数列形式的变形,数列的基础知识、基本技能仍然是考查的重点,例2、例3中都考查了等差数列的求和,例1、例4考查了等比数列的通项及等比数列、等差数列的求和,例1考查数列知识的同时,结合数幂及不等式的知识进行了考查,具有一定的综合性.上述数表问题在考查形式上,主要涉及的设问方式包括:求数表中的某项元素和数表求和. (2)关于数学思想方法的考查.数表问题重点考查转化与化归的思想方法,例如例2中将集合表达式的形式转换为数表的形式;例3中要求解第n行第3个数,可以将数表转化为数列的形式,则所求问题一目了然;例4中解题的关键是要将数列项a81转换为其在数表中的位置;例1的试题设计中,将转化与化归数学思想放到了更加突出的地位,例1与其他3道题目考查的都是关联数表的数列问题,在其他3道题目中数表的形式已经给出,而例1需要考生根据所给数列的特点将其转化为数表的形式,转化的思想是解题的关键.另外,与其他数表问题相比,例1考查了从特殊到一般的思想,在例2、例4中都考查了数表中的某一具体项的求值,而例1中需要求解的是任意第N项的表达式. (3)关于数学能力的考查.在高考数学命题中,坚持“能力立意”,能力考查的原则是,以思维能力为核心,全面考查各种能力.数列作为高中数学的重点内容,主要考查抽象概括能力、推理论证能力、运算求解能力、应用意识和创新意识.在上述数表问题的考查中,运算求解能力是基础,重点考查抽象概括能力和推理论证能力,对考生的创新意识也提出了较高要求.以例1为例,解答中涉及3个关键步骤,首先要将数列转化为数表形式,找出数列的规律,其次要求出前N项和SN的表达式,还要找出SN为2的整数幂的成立条件.第一步,找出数列的规律重点考查抽象概括能力和创新意识,第二步,求解SN的表达式考查了推理论证能力和运算求解能力,最后求证SN为2的整数幂的成立条件则对推理论证能力提出了更高层次的要求. 2017年理科数学全国卷I第12题中蕴含着丰富的数学思想方法,对考生的数学能力及学科素养都进行了深度考查,是一道优秀的高考试题.另一方面,从考生答题来看,试题具有较大难度,要答对这道选择题,并不容易,5分的分值蕴含了大量的思维过程.从应试的角度,对于大部分考生,为一道选择题压轴题占用大量的精力和时间,是得不偿失的,放弃解答随机选择一个答案也许是相当一部分考生的应对,这样对于精心命制的优秀题目无疑是一种浪费.因此我们希望将这道试题进行一定改编与创新尝试,以更好地突出其考查效果. 从不同题型在试卷中的作用来看,选择题、解答题均是数学试卷中的主要题型,同一个知识点对于不同题型的选择能够直接影响试题的信度、效度及区分度. 从高考的历史看,解答题的历史更为悠久,上世纪80年代随着教育测量学、教育统计学等的发展,我国开始研究实施以客观性试题为代表的标准化考试.从高考数学的历史看,1983年之前的高考数学是没有选择题这种题型的.选择题这种考查方式与解答题相比,具有自身的优点:如有利于扩大试卷容量,提高知识考查的覆盖广度;题意清楚,评分标准统一、准确,不受评卷者主观因素的影响,有利于提高考试的公平性、信度和效度;有利于培养学生思维的灵活性等;但选择题也存在着许多的考查局限性,例如不利于区分不同层次考生的差异;不能反映考生解题的思维过程,评分不一定能反映考生真实水平;不利于培养学生的表达能力等.因此在数学试卷中采用选择题与解答题相结合的考查形式,能够有效地形成互补,更加全面、有效地进行考查知识与能力. 从例1的解答来看,试题的难点体现在数列与数表的转换、SN的表达式求解、寻找SN与2的整数幂的关系.而作为选择题的考查,完全可以通过恰当的技巧与处理方式避开后两个难点,正如方法一,代入验证是选择题解答的常用方法,能够提高选择题解答的效率,将具体的N代入后求SN,只要能够将数列转化为数表,并归纳出规律,根据等差数列与等比数列知识不难求出具体的SN的值,也容易得出是否为2的整数幂,体现的是将抽象问题具体化的处理办法.这样的处理方式,解答思维量降低,但是试题的计算量有所增加,对考生的计算能力同样要求较高.同时,该题作为选择题压轴题,难度较大,根据对于选择题解答的研究,当选择题较容易时,就有较多的学生完成直接求解,特例法和猜测法都较少用,当题目较难时学生直接求解有困难,就更倾向于用特例法和猜测法,题目越难猜测成分越高,难度过高的选择题往往在区分度方面并不理想.解答题的优点恰好在于能够更好地体现考生的思维过程、区分不同层次考生.下面将该题改编成一道解答题.据此,该题可改编如下: 已知数列{an}={1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…},其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推. (Ⅰ)分别求a21,a110的值; (Ⅱ)求数列前110项的和S110; (Ⅲ)求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂. 改编为解答题后,为了降低试题难道,提高区分度,在原来问题的基础上设置了具有一定梯度和启发性的前2个问题.第Ⅰ问设置的是求特殊项的值,目的在于让考生通过数列特殊项的求值,发现数列的规律,将其转换为数表形式,其中a21,a110两项的设计考虑所求项具有一定的特殊性,a21恰好是第6组的最后一个,更有利于考生发现数列分组的规律,考生即使暂时没发现数表规律,通过逐一列举也不难找出,对于a110考生必须发现数列的规律后才能通过计算得出其所在数表中的位置,进而求得其值,且a110在第15组第5个,与a21所处的位置相比更具有一般性,更有利于引导考生在求解(Ⅲ)时,做出对N所在位置的恰当假设.第Ⅱ问,需要考生直接利用通过(Ⅰ)发现的数表规律求具体的前N项和,直接考查等比数列、等差数列知识的运用,为最终求解(Ⅲ)更进一步.(Ⅲ)由选择题转换为解答题后,将数列与不等式进行结合,对考生思维的严密性及逻辑推理能力提出了更高的要求. 题目的改编理念体现的是由特殊到一般的思想,最终求解的问题具有较大的难度,希望通过做铺垫、“架梯子”的方式为考生引路,同时也使不同层次考生均能够得到展现的机会. 关联数表的数列问题是数列考查的一种重要形式,历年高考中也多次出现,2017年再次出现,题目的形式和考查重点都具有了一定的创新性,充分体现了高考题目“重基础、重能力、重创新”的特点,在日常的教学研究中,要善于捕捉、吃透这样的“好题”,在课堂教学中以好题为抓手开展探究性学习,注重一题多解、多题一解,举一反三,注重通性与通法,注重数学思想方法的渗透和学科能力的培养,使这样的好题真正成为宝贵的财富.当然,有效解决这些题目的基础是以基础知识和数学思想方法为基础的有效教学,而并非题海战术和机械训练,能力立意的创新是这类题目设计的不变主题.

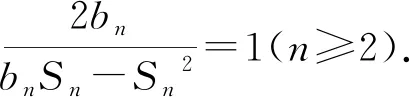


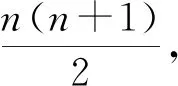
2.2 关联数表的数列试题命制分析
3 试题的创新命制探析
3.1 不同题型的功能分析
3.2 试题改编分析
4 结语

