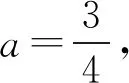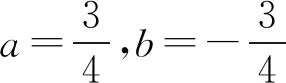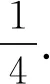关于含绝对值函数的双重最值问题的研究
童益民
(宁波效实中学 315012)
含绝对值的函数是高考中的一个考点,含绝对值函数的最大值问题是近年高考的热点,而含绝对值函数的最大值的最小值问题更是高考中的一个难点,如2015年浙江高考理科第18题,2016年天津高考理科第20题.本文通过对含绝对值的二次、三次函数的思考研究,得到一般的几个结论,以供读者参考.
思考1已知函数f(x)=x2+bx+c(b,c∈R)的定义域为[α,β],记|f(x)|的最大值为M,研究当f(x)满足什么条件时,M取到最小值?
分析:因为


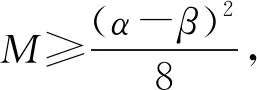
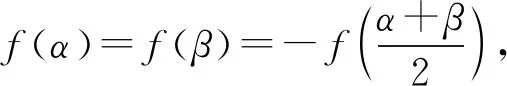

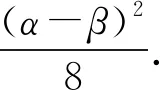
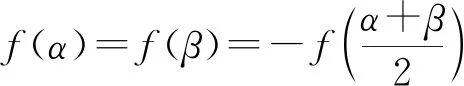
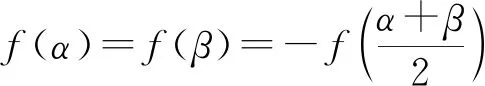
接下来进行类比.
思考2已知函数f(x)=x3+bx+c(b,c∈R)的定义域为[α,β](α<0<β),其中α+β=0,记|f(x)|的最大值为M,研究当f(x)满足什么条件时,M取到最小值?
分析:(1)当b≥0时,f(x)在[α,β]上单调递增,显然当-f(α)=f(β),即c=0 时,|f(x)|的最大值M取到最小值β3+bβ.
(2)当b<0时,
①若c=0,

f(β)=β3+bβ,
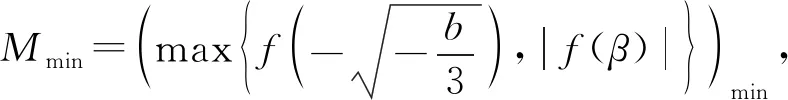
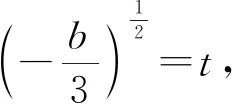
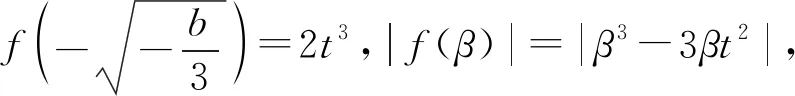
画出关于t的函数g(t)=2t3,h(t)=|β3-3βt2|的图像,如图1,

图1
当t=t0时,|f(x)|的最大值M的最小值为
②若c>0,

f(β)=β3+bβ+c,
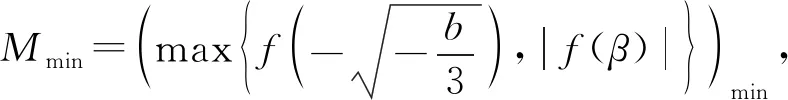
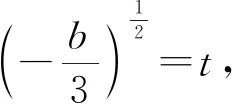
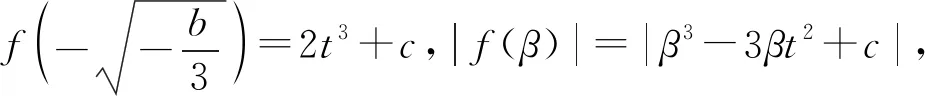
画出关于t的函数g(t)=2t3+c,h(t)=|β3-3βt2+c|的图像,如图2,

图2
当t=t0时,|f(x)|的最大值M的最小值为
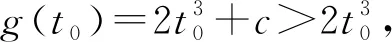
③若c<0,

f(α)=α3+bα+c,

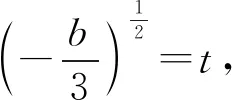

|f(α)|=|α3-3αt2+c|=|β3-3βt2-c|,
画出关于t的函数g(t)=2t3-c,h(t)=|β3-3βt2-c|的图像,如图3,
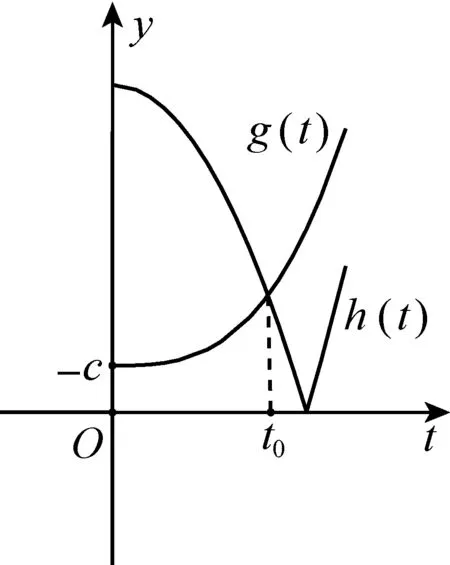
图3
当t=t0时,|f(x)|的最大值M的最小值为
舍去.由①②③得,

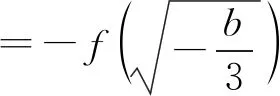
|f(x)|的最大值M取到最小值β3+bβ.
综上(1)(2)得,

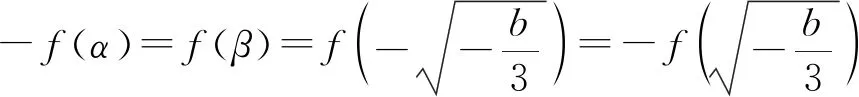
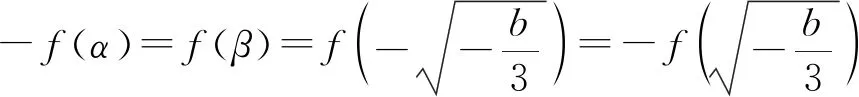
再进一步推广.
思考3已知函数f(x)=x3+ax2+bx+c(a,b,c∈R)的定义域为[α,β],记|f(x)|的最大值为M,研究当f(x)满足什么条件时,M取到最小值?
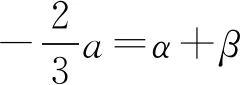
f(x)=x3+ax2+bx+c
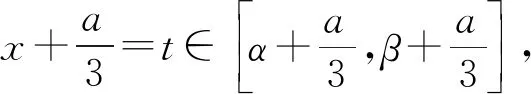
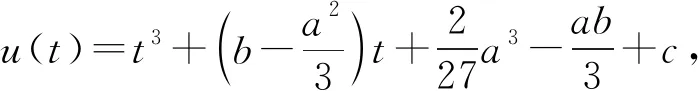
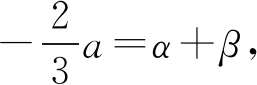
根据结论2,可得,
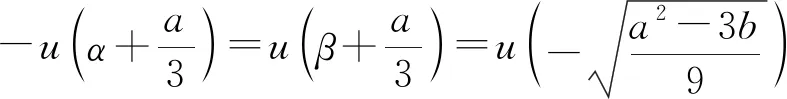
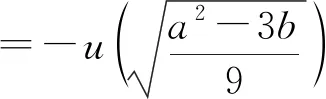
|u(t)|的最大值M取到最小值,
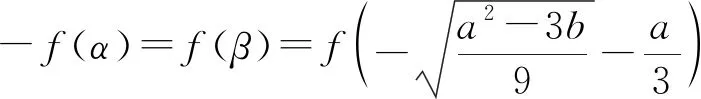
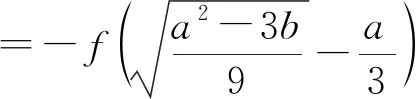
|f(x)| 的最大值M取到最小值.
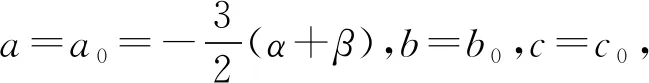
函数记为f0(x)=x3+a0x2+b0x+c0,
|f(x)|的最大值M取到最小值M0.
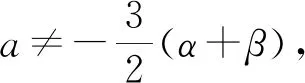
任取a=a1≠a0,b=b1,c=c1,
令f1(x)=x3+a1x2+b1x+c1,
则f1(x)=x3+a0x2+b0x+c0+(a1-a0)x2+(b1-b0)x+(c1-c0)
=f0(x)+(a1-a0)x2+(b1-b0)x+(c1-c0),

图4
令g(x)=(a1-a0)x2+(b1-b0)x+(c1-c0),
所以f1(x)=f0(x)+g(x),
因为函数f0(x)的图像如图4,
要使得函数|f1(x)|的最大值小于等于M0,

因为二次函数g(x)的二次项系数a1-a0≠0,显然是不成立的,
所以函数|f1(x)|的最大值大于M0,
|f(x)|的最大值M的最小值都大于M0.
综上(1)(2)得,
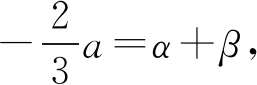
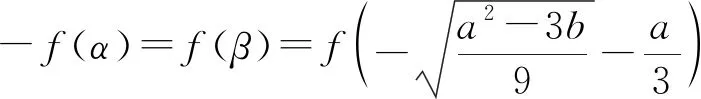
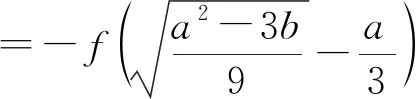
|f(x)|的最大值M取到最小值.
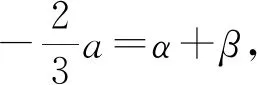
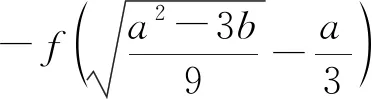
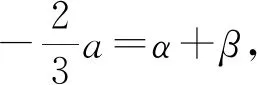
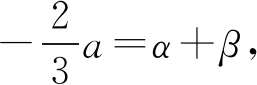
对于以上得到的三个结论,可以帮助我们在解此类题目时有一个整体的认识,可以灵活应用,同时也为用绝对值不等式解此类题时,取什么特殊值提供了方向,就是考虑区间的端点和极值点. 以下两题仅供参考.
题1已知函数f(x)=x2+bx+c(b,c∈R)的定义域为[0,2],记|f(x)|的最大值为M,求M的最小值.
解析:当f(0)=f(2)时,f(x)的极值点为x=1,可考虑取x=0,2,1.

所以4M≥|f(0)|+|f(2)|+2|f(1)|
≥|f(0)+f(2)-2f(1)|
=|c+4+2b+c-2-2b-2c|=2,
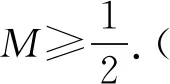

题2设函数f(x)=(x-1)3-ax-b,x∈R.其中a,b∈R.
解析:设x-1=t∈[-1,1],
则h(t)=t3-at-a-b,根据结论2,
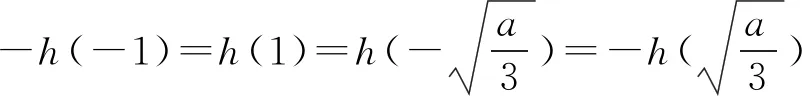
|h(t)|的最大值取到最小值.
由-h(-1)=h(1),得-a-b=0,