用几何眼光观察问题 有效提升运算素养
刘国祥
(江苏省宜兴中学 214200)
1 问题的提出
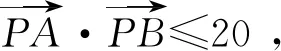
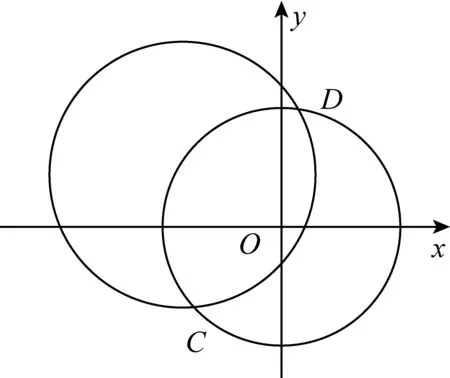
答题分析本题为2017年江苏高考第13题,满分5分,全省平均得分为1.3分,而错误答案中比率最高的答案为[-5,1].
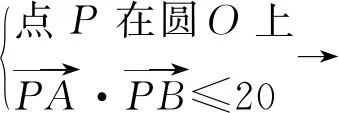
运算水平分析:2017版普通高中数学课程标准关于运算素养的水平划分为三个层次:(1)能够在熟悉的情境中了解运算对象,提出运算问题,并用运算结果说明问题;(2)能够在关联的情境中了解运算对象,提出运算问题,并能够借助运算探讨问题;(3)能够在综合情境中把问题转化为运算问题,明确运算方向,构建运算程序,能够用程序思想理解和解释问题.以上三个水平层次分别对应于对运算素养的三个要求:熟悉运算,转化运算,创新运算.本题经历两个过程,第一步过程是几何问题代数化,是将题中几何条件直译成代数关系,是熟练运算,是属于划分水平一层次,对学生来说不成障碍;第二步过程是从代数关系中抽象出几何问题和几何图形,利用圆与圆的位置关系结合图形特征来正确求解,需要对运算转化与创新,是属于水平二与水平三层次.从学生错误解答来看,问题主要出在第二步上,停留在代数层面运算,没有对问题进行转化,根源在于学生缺少 “用几何的眼光观察问题”的过程.
2 问题的探讨
解析几何的核心思想是用代数方法解决几何问题,解题程序为:抽象研究对象(几何问题或几何图形)→几何对象的代数表达(坐标法)→代数运算→代数结果的几何解释.
章建跃博士在“解析几何的思维方式与核心素养”一文中指出:“用几何眼光观察,分析清楚几何图形的要素及有关几何关系,再用代数的语言来表达,而且在代数运算中时刻注意利用它们来简化运算,这就是解析几何运算的特点,是几何背景下的代数运算,是解析几何的思维方式”[1].当下解析几何的运算已经成为学生学习的难点,其根源在于学生缺少“用几何的眼光观察问题”的意识和能力,从几何角度对面临问题分析不充分,对几何图形的要素及其基本关系理解不到位,把坐标法异化为纯粹代数运算,造成运算过程复杂化.如何突破解析几何运算的难点,实现运算素养由水平一向水平二、三的转化?笔者的体会是:要善于用几何的眼光观察问题,努力提高几何图形的分析能力,在落实数形结合上下功夫.
2.1 用几何的眼光统整题目条件,优化运算路径



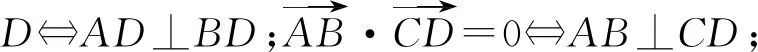
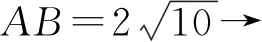

评析思路一对条件中信息不作任何转化直接翻译,解法繁琐,运算量大,解题方法平淡,属于运算水平一,是大部分考生首选方法,导致本题得分较低;思路二,从几何的视角对条件中的信息进行发散、整合,深入挖掘,得到更多信息,其中程序一统整到△AOB中,转化为解三角形问题;程序二的关键是发现:△BOD是一个定三角形,使问题的求解简单自然.思路二是属于在综合情境中用数学的眼光将条件统整到一个三角形中显化问题的本质,是属于转化运算、创新运算.
教学启示首先在解题教学中要强化数学语言的转化,数学问题的呈现多采用文字语言和符号语言,在审题时善于将抽象的符号语言转化成文字语言,再转化为直观的图形语言;其次将条件整合到图形中,有利于发现各几何要素之间关系,把握问题的本质;最后对图形进行综合分析用用代数的方法来解决几何问题.
2.2 用几何的眼光观察代数结构,探究运算方向
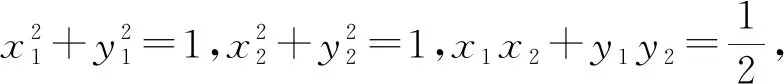
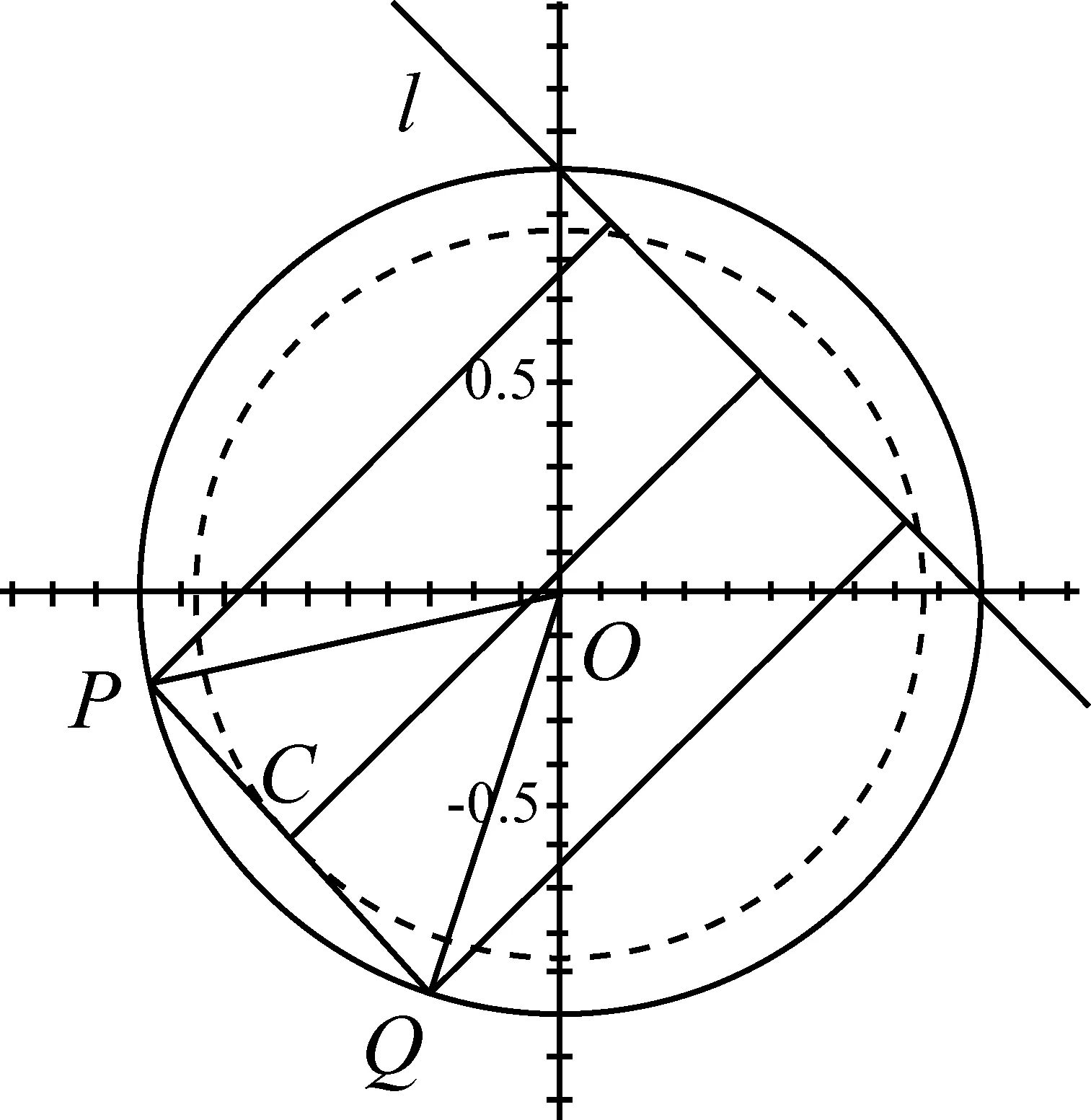
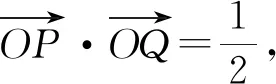
教学启示用几何的眼光观察代数式结构,首先在教学中要重视定义、公式、概念的多元表征,善于从代数和几何视角来表征,例如代数式x2+y2,从代数角度来说是实数x,y的平方和,从几何视角表示OP2(其中P(x,y));其次,在解题教学中学会联想,由代数结构会联想到几何形态;最后依据条件与结论构建合适图形创造性解决问题.
2.3 用几何的眼光审视动点规律,简化运算程序
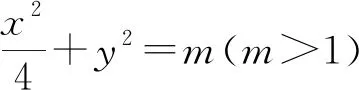
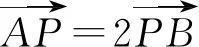
运算程序一:以m为变量,将点B的横坐标表示为m的目标函数.
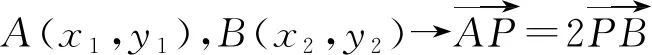
运算程序二:把直线AB变化源于直线斜率k视角来看,可以把点B的横坐标用直线斜率k来表示.
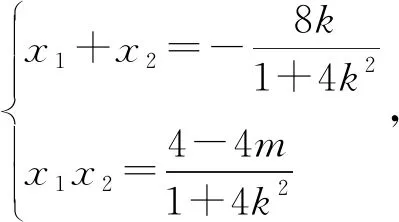
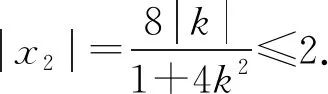
思路三:可以看作当点A在椭圆上运动时,求点B的轨迹方程.

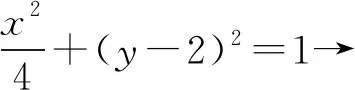
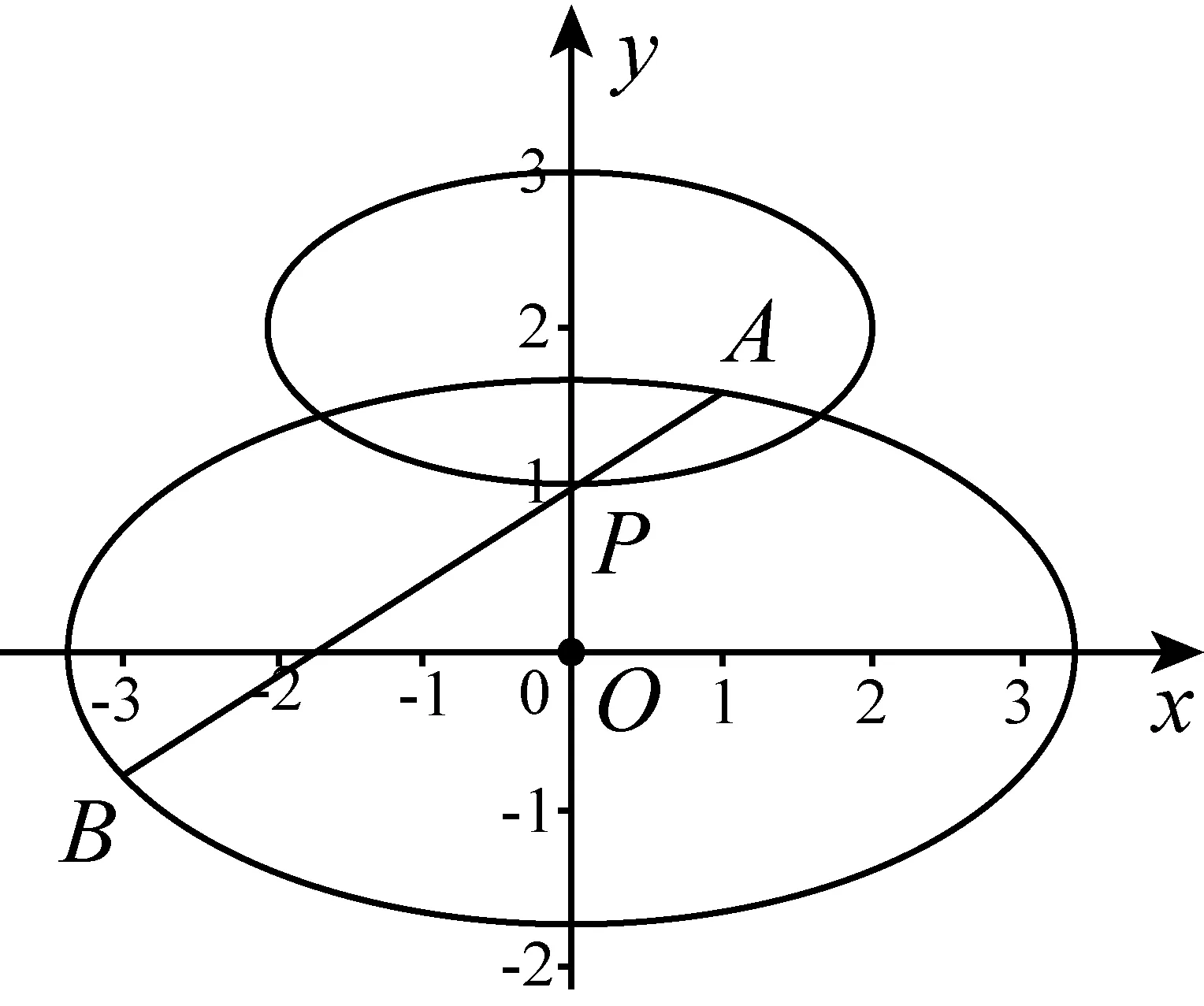
点评用几何的眼光观察问题,从向量视角来看容易生成运算程序一;从直线是过定点的直线,变化根源是倾斜角,容易生成运算程序二和三;当把A看作主动点,由此引发点B变化,容易生成运算程序四,从不同视角看动点会生成不同精彩的解法,将这些众多的解法进行比较分析,可以发现不同解法的优劣,从而可以得出减少运算量的解题程序,实现简化运算、提升速度的目标.
教学启示动态问题是解析几何中常见问题,解决动态问题关键是分析动点变化规律,如上案例中从不同视角去研究变动原因产生了不同的解法.要找到动点变化的规律需要用几何的眼光来审视条件,回规问题本质.如2015年江苏高考第10题:在平面直角坐标系xOy中,以点(1,0)为圆心且与直线mx-y-2m-1=0 相切的所有圆中,半径最大的圆的标准方程为________.问题关键就是从几何视角来看是过定点(2,-1)的动直线,从几何上找到解决问题思路.
2.4 用几何的眼光发现几何特征,选择运算方法

本题关键是依据图形特点,合理选择面积表达.让学生思考3分钟,谈一谈如何表征面积.
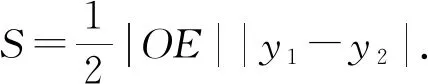
思路三:因为△OBC的底边OB为定值,选择OB为底,C到OB距离为高建立面积表达式.
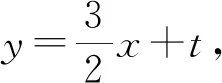
评析上述四种中哪种方案运算更合理呢?因为△OBC中O,C是定点,面积表征,显然是思路三和思路四更合理一些.
教学启示解析几何的本质是几何,图形是几何的直观表现形式,是问题的出发点和归宿点,而代数方法仅仅是工具,审视图形的整体结构,看穿图形的本质特征,就能化繁为简.
3 结语
高中数学教学活动要树立以发展学生数学核心素养为导向的教学意识,创设有利于学生数学核心素养发展的情境,引导学生把握数学知识的本质.就解析几何的教学而言,由于其学科本质是运用代数方法解决几何问题,能灵活地进行数与形的有机结合与相互转化,通过运用不同的视角探索解题的途径、优化运算的过程来提升和发展学生的运算素养是我们在教学中需要着力解决的问题.2017版高中数学课程标准对解析几何的“学业要求”是:依据问题情境分析几何问题和图形特点;依据几何问题和图形特点,探索解决问题思路;依据几何问题特点将几何问题转化为代数问题;运用代数方法推演结果并给出合理地几何解释.在解析几何教学中始终坚守学科大概念:用几何的眼光观察问题,借助几何图形的特点,形成解决问题思路,通过直观想象和代数运算得到结果,给出几何解释,解决问题,在这个过程中提高学生的思维品质,发展学生的关键能力,提升学生的运算素养,将数学核心素养的培养落到实处.

