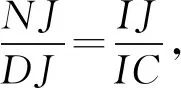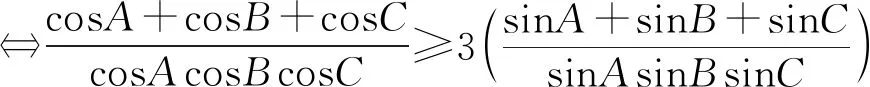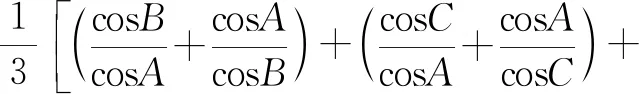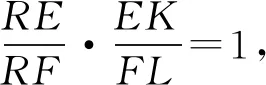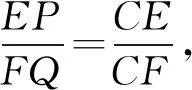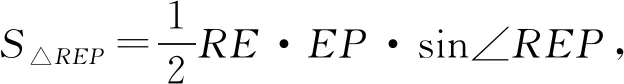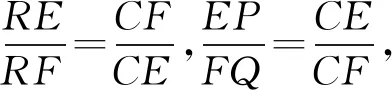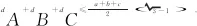数学问题解答
2019年10月号问题解答
(解答由问题提供人给出)
2506在k边形A1A2…AK(k≥3)中,a1,a2,…,ak为其各边长,s为周长,n∈N+且n≥2,0<λ≤1,求证:
(安徽省岳西中学 储百六 246600)
证明先证一不等式:当x∈[0,1]时,
(1)

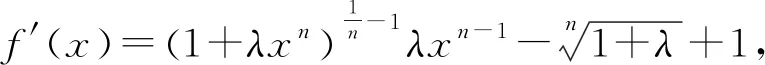

所以f′(x)在[0,1]上为增函数,


所以存在x0∈(0,1),使得f′(x0)=0,于是
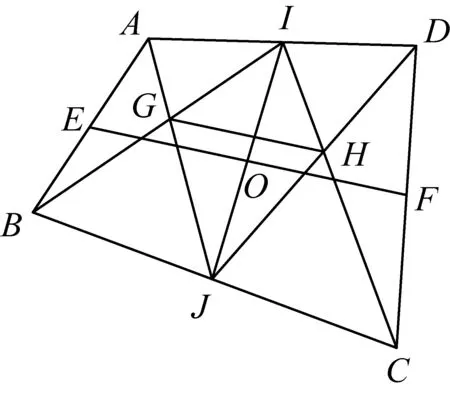
当0 当x0>1时,f′(x)>0, 所以f(x)在[0,x0]上为减函数,在[x0,1]上为增函数; 所以,当x∈[0,1]时,f(x)≤max{f(0),f(1)}=0,故(1)式成立 再将这k个式子相加可得 2507如图,已知四边形ABCD,E、F、I、J分别是四边的中点,分别连接AJ、IB、DJ、IC交G、H,IJ、EF交O,求证:GH∥EF. (江西师范高等专科学校 王建荣 335000) 证明如图,设AJ、DJ、IB、IC分别交EF于M、N、K、L,连AO、BO、IM、IN,由梅氏定理, △IKO、△ILO分别被直线GMJ、HNJ所截, 如果 2508在锐角△ABC中,有 (天津水运高级技工学校 黄兆麟 300456) 证明首先证明两个必要的不等式 (2) (3) 即有 (4) 同理有 (5) (6) (4)+(5)+(6)整理即得(2)式成立.下面再证(3)式成立. 利用熟知的三角恒等式 tanAtanBtanC=tanA+tanB+tanC, 我们可得 ⟺(cosA+cosB+cosC)tanAtanBtanC ≥3(sinA+sinB+sinC) ⟺(cosA+cosB+cosC)(tanA+tanB+tanC) ≥3(sinA+sinB+sinC) 记以上最后一式为不等式(7),即有(3)⟺(7). 由于不等式(7)的全对称性,不妨设A≥B≥C, 则有sinA≥sinB≥sinC, 那么由切比雪夫不等式,立得 ≥2(sinA+sinB+sinC), 即不等式(7)成立,从而不等式(3)也成立. 最后证明不等式(1)成立. (2)+2×(3)立得 两边开方即得不等式(1)成立. 2509如图1:在△ABC中,∠BCA的平分线与△ABC的外接圆交于点R,∠BCX=∠ACY,边BC的垂直平分线交CX于点P,边CA的垂直平分线交CY于点Q,K是BC的中点,L是AC的中点,则△RPK和△RQL面积相等. 图1 (安徽省旌德中学 赵忠华 242600) 证明如图2,如果AC=BC,则△ABC是等腰三角形,则△RPK和△RQL关于角平分线CR是对称的,结论明显成立. 图2 如果AC≠BC,不妨设AC 用O表示△ABC的外心, 注意到Rt△CLF∽Rt△CKE, 则∠CEK=∠CFL=∠OFE, 设l是弦CR的垂直平分线,则l过外心O, 由于△OEF是等腰三角形, 所以E,F是CR上关于l对称两点, 故RE=CF,RF=CE.(2) 又∠REK=∠RFL,所以S△REK=S△RFL.(3) 又∠REP=∠RFQ,所以S△REP=S△RFQ.(4) 由(3)-(4)可得S△RPK=S△RQL. 2510已知a,b,c>1,a+b+c+2≥abc,求证: (陕西省咸阳师范学院教育科学学院 安振平 712000) 注意到,当a≥b≥c>1,时,有 于是,应用切比雪夫不等式,得 2019年11月号问题 (来稿请注明出处——编者) 2511已知△ABC的角A,B,C的角平分线分别交边BC、AC、AB的垂直平分线于D、E、F,求证:△ABC的周长≤△DEF的周长. ( 山东省泰安市宁阳第一中学 刘才华 271400) 2512已知正数a,b,c,d满足abcd=1,求证: (安徽省岳西县汤池中学 杨续亮 苏岳祥 246620) 图1 2513如图1,分别以△ABC边AB、AC为一边向△ABC外作矩形ABDE和矩形ACFG,CD交BF于点P.若AB=kAE,AC=kAG,直线AP分别交BC、EG于点M、N.求证: (1)MN⊥BC.(2)点N是EG的中点. (四川省巴中市巴州区大和初中 李发勇 636031) (四川省成都华西中学 彭艳玲 张云华 610051)