挖掘“特殊”信息 “秒杀”中考小题

文

（作者单位：江苏省南京市天景山中学）

“二次函数”是各地中考考查的核心知识。如何在有限的考试时间内准确、快速地解题，是大家关注的焦点。下面结合几个例子和同学们一起分享。

一、二次函数图像的平移

例1 （2019·绍兴）在平面直角坐标系中，抛物线y=（x+5）（x-3）经变换后得到抛物线y=（x+3）（x-5），则这个变换可以是（ ）。

A.向左平移2个单位

B.向右平移2个单位

C.向左平移8个单位

D.向右平移8个单位

【分析】方法1：可以将该二次函数的表达式化为顶点式，根据顶点坐标的变化找出变换规律。方法2：由题给出的两个表达式，都是“交点式”，即变换前后与x轴交点分别为：变换前（-5，0）、（3，0），变换后（-3，0）、（5，0），显然这种解法较为简便。

【答案】B。

二、二次函数图像上点的坐标特征

例2（2019·福建）若二次函数y=+bx+c的图像经过A（m，n）、B（0，y1）、C（3-m，n）、D（ 2 ，y2）、E（2，y3），则y1、y2、y3的大小关系是（ ）。

A.y1＜y2＜y3B.y1＜y3＜y2

C.y3＜y2＜y1D.y2＜y3＜y1

【分析】由点A（m，n）、C（3-m，n）的对称性，可求函数的对称轴为x注意二次项系数为 ||a这个重要条件，可知该抛物线开口向上，可不必代入求值，由B（0，与对称轴的距离，即可快速判断。

【答案】D。

三、二次函数与一元二次方程

例3 （2019·武汉）抛物线y=ax2+bx+c经过点A（-3，0）、B（4，0）两点，则关于x的一元二次方程a（x-1）2+c=b-bx的解是_______。

【分析】从一元二次方程a（x-1）2+c=bbx出发，可化为a（x-1）2+b（x-1）+c=0。因A、B两点是抛物线与x轴的交点，即令y=0代入得：ax2+bx+c=0。对比可发现，（x-1）是一个整体，可得x-1=-3，x-1=4。

【答案】x1=-2，x2=5。

四、二次函数的最值

例4 （2019·内江）若x、y、z为实数，且则代数式x2-3y2+z2的最大值是_______。

【分析】从条件入手，发现此方程组解不出来。但从问题出发，发现求代数式x2-3y2+z2的最大值问题，可转化为求二次函数的最值问题，将代数式化为用同一个字母表示的形式就可以构造二次函数，解题思路得以打通。

【答案】26。

五、二次函数的综合运用

例5 （2019·潍坊）如图1，直线y=x+1与抛物线y=x2-4x+5交于A、B两点，点P是y轴上的一个动点，当△PAB的周长最小时，S△PAB= ______________。

图1

【分析】因交点A、B两点坐标可求，得AB=3 2。再从未知出发分析，要求△PAB的周长最小值，即可转化为求PA+PB的最小值，根据“将军饮马”模型，P点应是点A关于y轴的对称点A′与点B的连线与y轴的交点（如图2），因此点P坐标可求出为再根据y=x+1的图像与x轴的夹角为45°这一特性，可过P作AB边上的高，求出即可，本题迎刃而解。

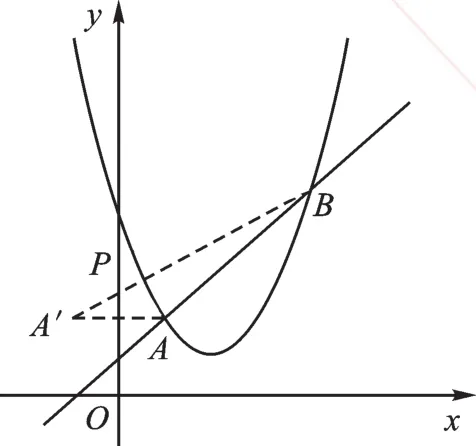
图2

【答案】

【点评】本题不仅考查了二次函数的性质，还考查了两点间的距离计算、一次函数的性质、轴对称（最短路径问题）。解决此类“小综合题”的关键是明确题意，发掘“线索”，结合图形，正确计算。

考试是有时间限制的，对于二次函数考点中出现的选择、填空这一类中档题，除能正确解题外，同学们还应追求更灵活、快速的解决方法，这样可以给解决后面的难题留下更多的时间。认真审题，在已知和未知中充分挖掘特殊的信息，找到解题的“关键因素”是考试成功的前提。