二次函数中的最值问题

文陈 卓

（作者单位：南京师范大学附属中学江宁分校）

最值问题的研究，有着悠久的历史。早在古希腊时，就研究了“等周问题”。在欧几里得的著作《几何原本》中，实际上已证明了如下的最值问题：具有相同周长的矩形中，正方形的面积最大。研究函数的最值，是学习数学与其他学科的基础，是生活生产的必备工具。二次函数的最值问题也是中考的热点内容之一，今天我们就一起来认识一下吧。

初中阶段确定二次函数y=ax2+bx+c（a≠0）最值的方法：

方法1：将二次函数y=ax2+bx+c（a≠0）配方化为y=a（x-h）2+k的形式，顶点坐标为（h，k），对称轴为直线x=h。若a＞0，y有最小值，当x=h时，y最小值=k；若a＜0，y有最大值，当x=h时，y最大值=k。

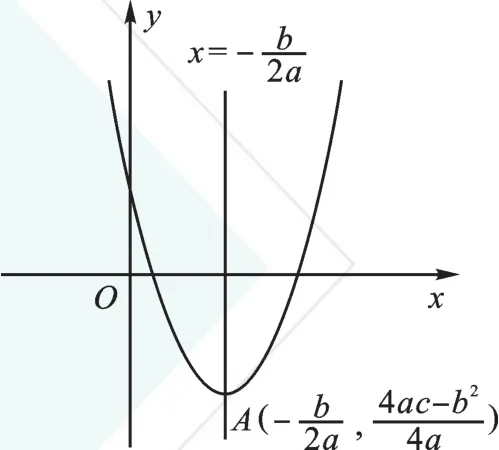
1.自变量x没有范围限制，可以取到整个实数。这时抛物线的顶点对应的y值是这个函数的最值，也就是说，当x取抛物线的对称轴的值时，即时，所得的y值是这个函数的最值。

2.自变量x有范围限制，它只能取到抛物线的一部分，这时需要判断x能够取到的范围是否包括抛物线的对称轴x=如果包括，那它的一个最值一定在对称轴处得到（最大值还是最小值要由a的正负判断，a正就是最小值，a负就是最大值）。另外一个最值出现在所给范围的端点，此时可以把两个端点值都代入函数，分别计算y值，比较一下就可以。如果

二次函数的图像是一条抛物线，根据实际情况它的最值又分为以下几种情况：

给的是代数形式，也可以用与对称轴距离的大小来判断，与对称轴距离大的那个端点能够取到最值。如果x的取值范围不包括对称轴，则它的最值一定出现在范围的端点处。当a＞0时，离对称轴最远的端点取得最大值，最近的端点取得最小值；当a＜0时，离对称轴最远的端点取得最小值，最近的端点取得最大值。

例1 （2018·黄冈）当 a≤x≤a+1时，函数y=x2-2x+1的最小值为1，则a的值为（ ）。

A.-1 B.2 C.0或2 D.-1或2

【分析】利用二次函数图像上点的坐标特征找出当y=1时x的值，结合当a≤x≤a+1时函数有最小值1，即可得出关于a的一元一次方程，解之即可得出结论。

解：当y=1时，有x2-2x+1=1，

解得：x1=0，x2=2。

∵当a≤x≤a+1时，函数有最小值1，

∴a=2或a+1=0，

∴a=2或a=-1，

故选：D。

【点评】本题考查了二次函数图像上点的坐标特征以及二次函数的最值，利用二次函数图像上点的坐标特征找出相应的值是解题的关键。

例2 （2018·潍坊）已知二次函数y=-（x-h）2（h为常数），当自变量x的值满足2≤x≤5时，与其对应的函数值y的最大值为-1，则h的值为（ ）。

A.3或6 B.1或6

C.1或3 D.4或6

【分析】分h＜2、2≤h≤5和h＞5三种情况考虑：当h＜2时，根据二次函数的性质可得出关于h的一元二次方程，解之即可得出结论；当2≤h≤5时，由此时函数的最大值为0与题意不符，可得出该情况不存在；当h＞5时，根据二次函数的性质可得出关于h的一元二次方程，解之即可得出结论。

解：当h＜2时，-（2-h）2=-1，

解得：h1=1，h2=3（舍去）；

当2≤x≤5时，y=-（2-h）2的最大值为0，不符合题意；

当h＞5时，-（5-h）2=-1，

解得：h3=4（舍去），h4=6。

综上所述：h的值为1或6。

故选：B。

【点评】本题考查了二次函数的最值以及二次函数的性质，分h＜2、2≤h≤5和h＞5三种情况求出h值是解题的关键。

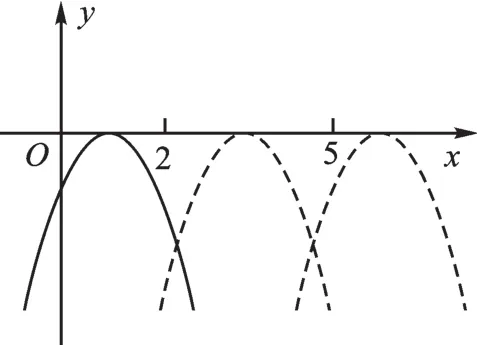
例3 （2017·乐山）已知二次函数y=x2-2mx（m 为常数），当-1≤x≤2时，函数值y的最小值为-2，则m的值是（ ）。

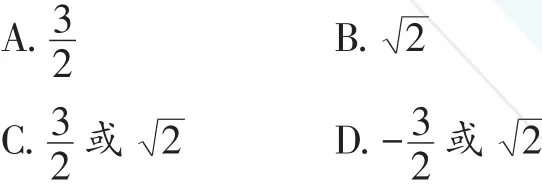
【分析】将二次函数配方成顶点式，分m＜-1、m＞2和-1≤m≤2三种情况，根据y的最小值为-2，结合二次函数的性质求解。

解：y=x2-2mx=（x-m）2-m2，

①若m＜-1，当x=-1时，y=1+2m=-2，

②若m＞2，当x=2时，y=4-4m=-2，

③若-1≤m≤2，当x=m时，y=-m2=-2，

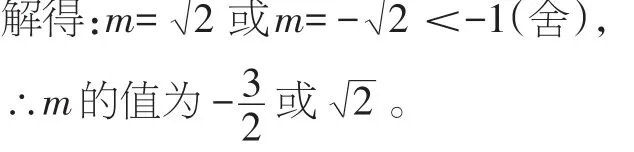
故选：D。

【点评】本题主要考查二次函数的最值，根据二次函数的增减性分类讨论是解题的关键。

例4 （2019·铁岭）小李在景区销售一种旅游纪念品，已知每件进价为6元，当销售单价定为8元时，每天可以销售200件。市场调查反映：销售单价每提高1元，日销量将会减少10件。物价部门规定：销售单价不能超过12元。设该纪念品的销售单价为x（元），日销量为y（件），日销售利润为w（元）。

（1）求y与x的函数关系式。

（2）要使日销售利润为720元，销售单价应定为多少元？

（3）求日销售利润w（元）与销售单价x（元）的函数关系式，当x为何值时，日销售利润最大，并求出最大利润。

【分析】（1）根据题意得到函数解析式；

（2）根据题意列方程，解方程即可得到结论；

（3）根据题意得到w=（x-6）（-10x+280）=-10（x-17）2+1210，根据二次函数的性质即可得到结论。

解：（1）根据题意得，

y=200-10（x-8）=-10x+280。

（2）根据题意得，（x-6）（-10x+280）=720，解得：x1=10，x2=24（不合题意舍去）。

答：要使日销售利润为720元，销售单价应定为10元。

（3）根据题意得，w=（x-6）（-10x+280）=-10（x-17）2+1210，

∵-10＜0，

∴当x＜17时，w随x的增大而增大，当x=12时，w最大=960。

答：当x为12元时，日销售利润最大，最大利润960元。

【点评】此题考查了一元二次方程和二次函数的运用，利用“总利润=单个利润×销售数量”建立函数关系式，进一步利用二次函数的性质解决问题，解答时求出二次函数的解析式是关键。

总之，二次函数的最值问题是一个在充分理解题意的基础上，综合运用各种方法进行解答的过程。通过这方面的学习，同学们能感受到数学的严谨、最值的合理。