工程浮吊浅水系泊定位时域运动分析

何晓宁 刘亚东

（1.上海交通大学 船舶海洋与建筑工程学院 上海200240；2.招商局邮轮制造有限公司 海门226116）

引 言

工程浮吊一般用于码头和遮蔽海域的海工设备安装、海上风电场安装、桥梁吊装、海上事故救援等，是海洋工程重点装备，而船舶系泊定位的可靠性同吊装安全息息相关，因此对于船舶在外力作用下的运动研究和预测非常重要。

以锚链系泊工程浮吊为研究对象的文章不多，其中万浩、杨新权等［1］完成了12 000 t 回转浮吊的水动力分析，得到了吊物运动和船体运动随不同参数变化的规律，对作业环境水域限制进行了分析；刘丹等［2］分析了锚泊定位的大型挖斗船的时域耦合分析，对挖斗操作过程中的系泊张力进行了分析。根据已查阅的资料，国外针对浮吊的研究极少，对深水海洋装备和多船关联耦合研究较多。本文研究对象为扒杆式工程浮吊，作业区域主要是港口和码头浅水区域（<40 m），考察在此类环境条件下的船舶运动特征，为船舶操纵提供指导依据。

本船船体主体为箱型，首尾呈楔形，吊臂为扒杆式，由人字架、臂架支架和主臂架组成（如图1）。

图1 浮吊效果图

该船的主尺度见表1。

系泊系统采用8 台系泊绞车，连接钢丝绳、锚链和锚构成，典型的系泊状态为8 点发散型布置，见图2。

本文对浮吊在系泊状态下受到的外部波浪力、风流力和系泊力进行频域分析，求得水动力参数并建立运动方程，运用数值模拟方法求解运动微分方程，得到浮吊在外力和系泊力联合作用下的时域运动；然后对结果进行分析，总结浮吊运动特性，为吊装稳定性和安全操作提供指导和依据。

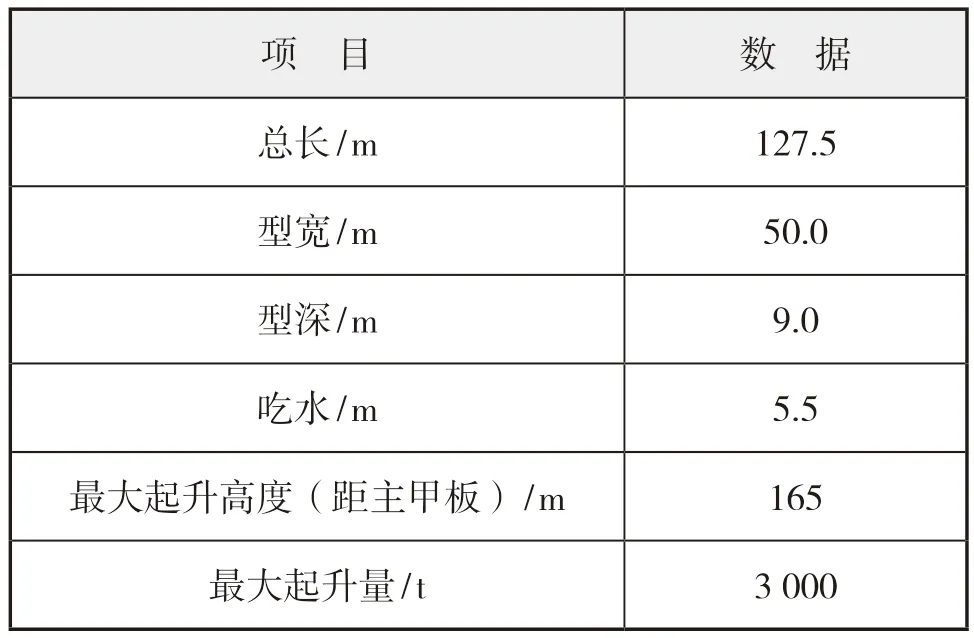
表1 浮吊主参数表

图2 浮吊系泊缆布置图

1 理论模型与参数选取

1.1 坐标系

坐标系采用右手坐标系，也是常用的船舶坐标系，如图3 所示。

图3 船舶坐标系示意图

1.2 风流力载荷

风流力载荷考虑为定常载荷，采用经验公式计算。

1.2.1 流力的计算公式

式中：F为水流力，N ；Cf为摩擦力系数，为无量纲数；ρ0为流体密度，kg/m3；u为水流速，m/s；A为受流力投影面积，m2。

本例中横向水流力计算：

纵向水流力计算：

式中：流速u取1.1 m/s；平板物体形状系数Cf取1.0；A= 522 m2； 密度ρ0取102.4×10-3kg/m3。

1.2.2 风载荷的计算公式

根据本船的作业条件，海况采用蒲式5 级以下，风速取≤10.7 s、流速取≤1.1 m/s、平板物体形状系数CS取1.0，且认为风流同向，并且和波浪运动方向相同为最危险情况。

根据浮吊的几何形状，可以计算横向受力如表2。

其他方向可以此类推。

表2 横向风力计算表

1.3 波浪载荷

1.3.1 势流理论和波浪力计算

本文采用势流理论对波浪力进行计算，并采用数值分析的方法求解船舶运动响应。采用势流理论求解大尺度结构物所遭受的水动力载荷，假设结构物附近的流场是无黏性的（即无旋有势），速度势是空间位置和时间的函数，应满足连续性方程，即速度势必须满足拉普拉斯控制方程，见式（3）：

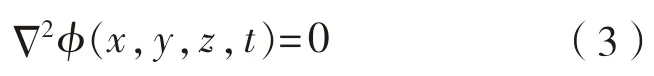
它在直角坐标系中的表达式见式（4）：

拉普拉斯方程和相应的边界条件都是线性的，可应用叠加原理把速度势加以分解。令速度势为

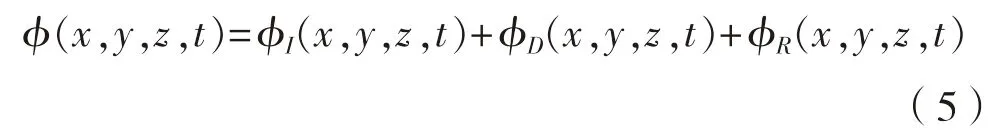
1.3.2 波浪谱

不规则波浪采用JONSWAP 波浪谱进行模拟，JONSWAPS 谱适用于有限风区的情况：

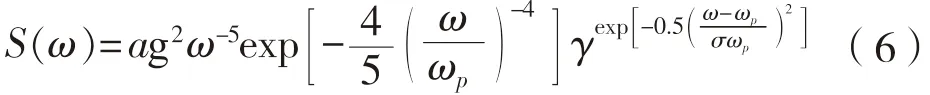
式中：ωp为谱峰频率，Hz；g 为重力加速度，m/s2；α为广义菲利普常数=γ为谱峰值参数。

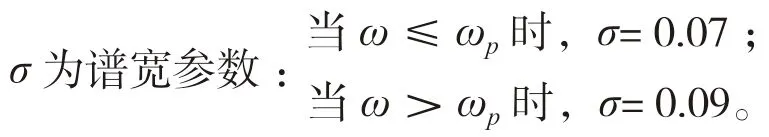
根据本船所处的环境条件，波普选用Jonswap谱：谱峰周期取0.7s，有义波高取1m；波浪谱图如图4 所示。考虑到船的对称性，考察如下5 个浪向：0°（迎浪）、45°、90°（横浪）、135°、180°（随浪）。

图4 波谱图

1.4 系泊力模拟

采用悬链线理论对系泊力进行简化处理（如图5），悬链线系泊缆的平衡方程是：

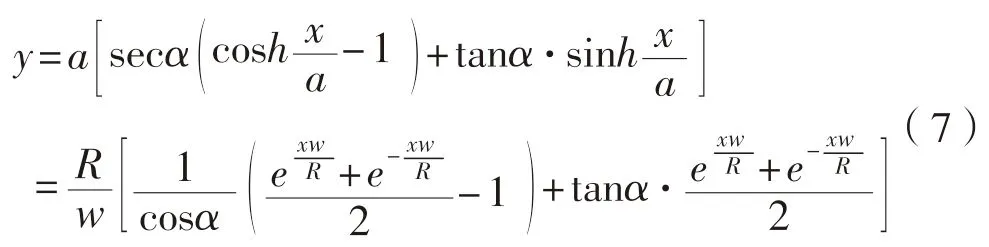
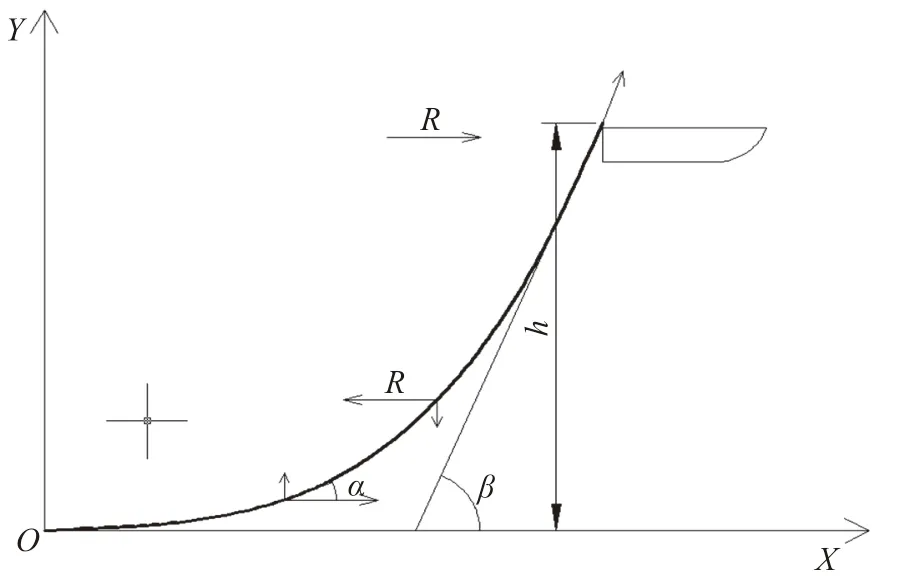
图5 悬链线示意图

式中：y为水深，m；R为作用在船上的外力，N；x为锚泊点至挂链点的水平距离，m；α为起锚角，°；w为每米链重，kg/m。

从以上公式中可以看出y是R，x，α，w的函数，即已知R，x，α，w就可以求得水深y。

系泊力根据目前的锚链配置，进行系泊力反算。实际上船舶抛锚时， 通常设置有足够长度的锚链， 以便有一段躺底锚链， 使锚不产生上拔力， 即α= 0°； 而如果又选定了锚链， 则每米链重w也为常量（本船采用56 AM3 锚链，单位长度重68 kg/m）；本船作业环境＜40 m，水深y取40 m。根据码头作业条件，假设抛锚点与导缆器的距离x为400 m。x值代入公式（7），求得作用在导缆器滚轮的力为1 360 kN，同时x每增加1 m，拉力变化约为10 kN。

1.5 船舶运动方程

对于系泊状态下的受风浪流和波浪联合作用下的浮体，有如式（8）所示运动方程：

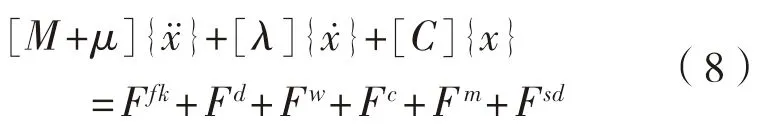
式中：［M］为浮体的广义质量矩阵，kg；［μ］为浮体的附加质量阵，kg；［λ］为阻尼系数阵（无量纲）；［C］为静水恢复力矩阵，N/m；别为广义加速度列阵以及广义速度列阵，为广义位移列阵，m。F f k为佛汝德-克雷洛夫力（Froude-Krylov）、F d为波浪绕射力、F w为风力、F c为流力、F m为系泊力、F sd为波浪二阶漂移力，单位均为N。

2 计算结果分析

不同波浪方向的船舶运动时历响应图，如图6-图11 所示。

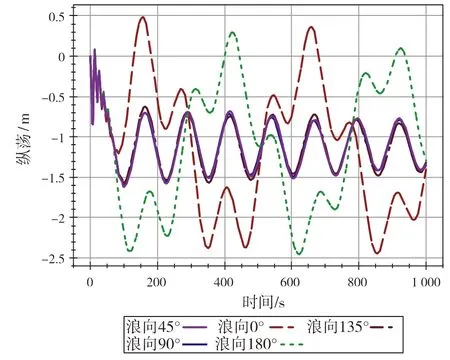
图6 纵荡时域响应图

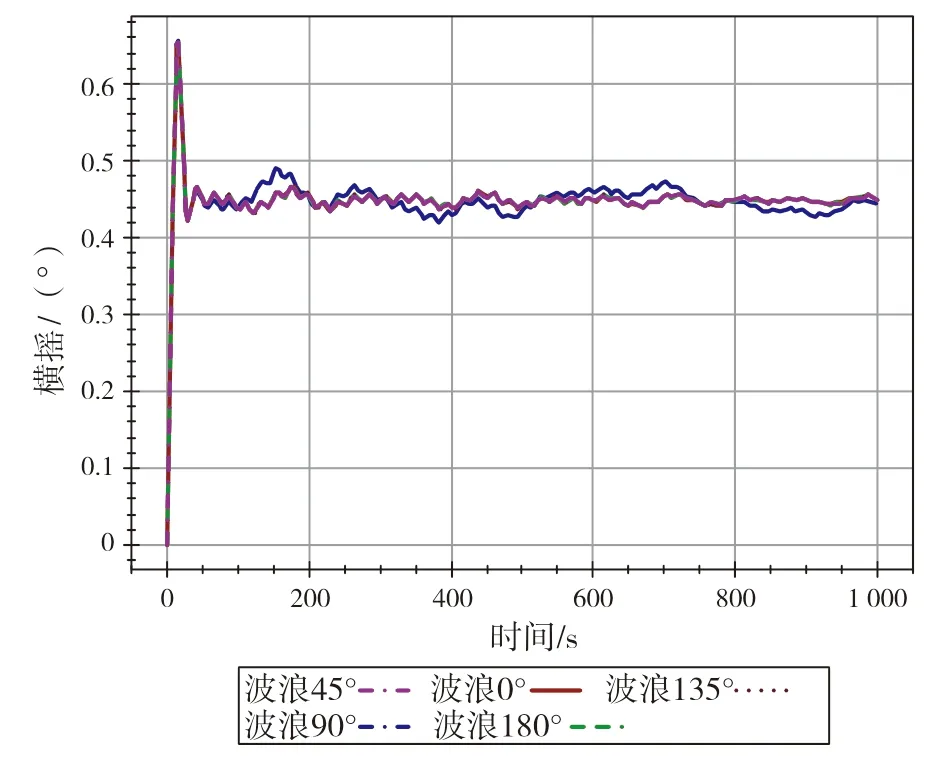
图7 横摇时域响应图

图8 横荡时域响应图

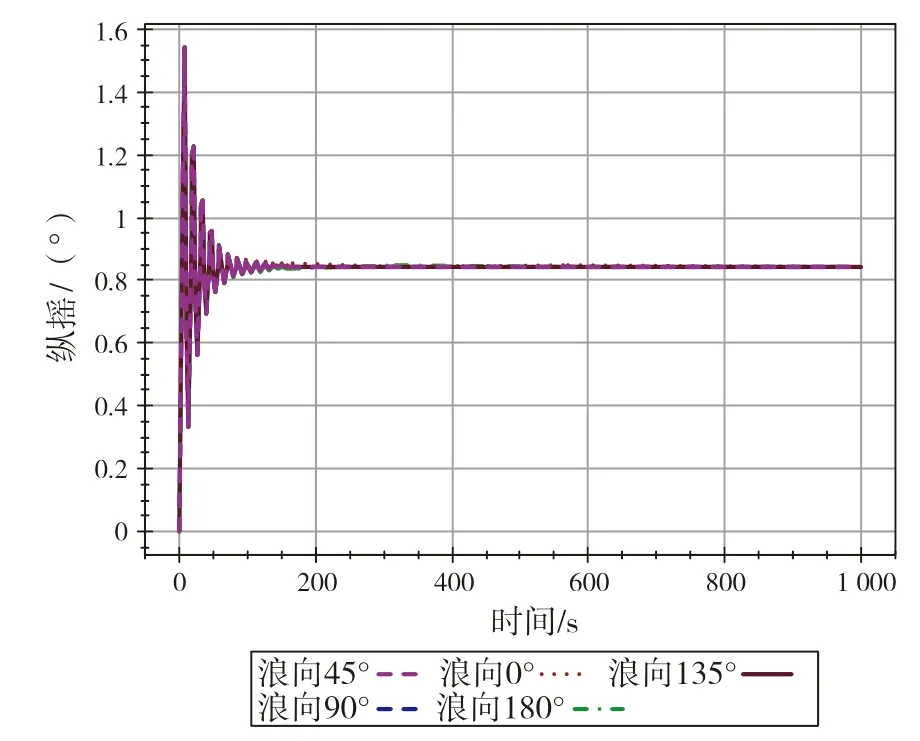
图9 纵摇时域响应图

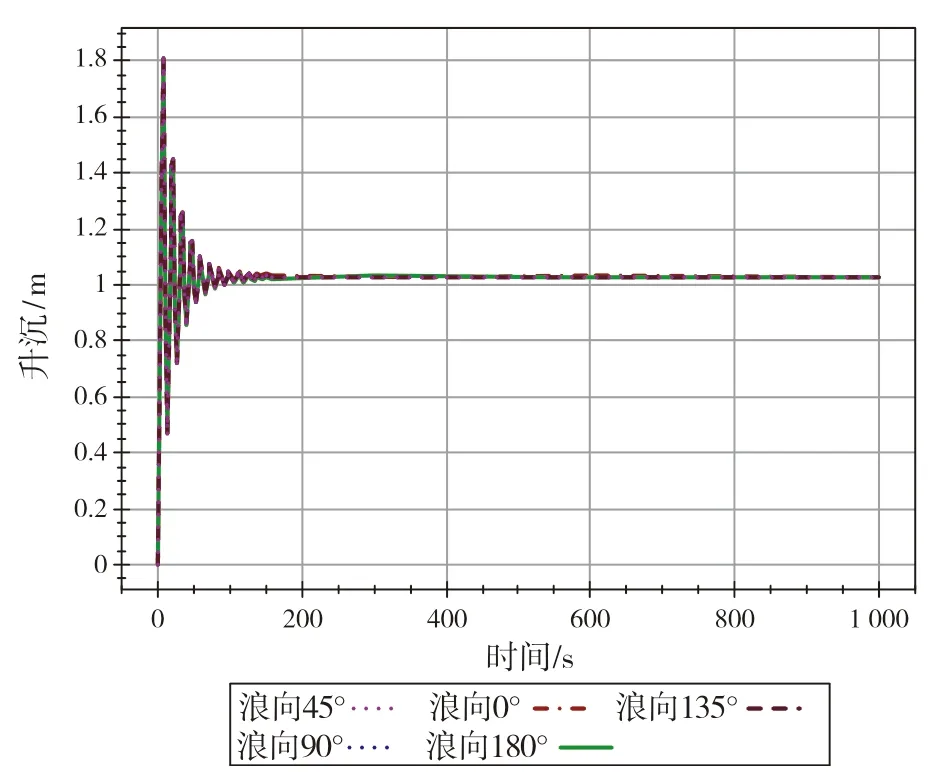
图10 升沉时域响应图

由时历曲线可见，6 个自由度运动中，纵荡和横荡在某些浪向下呈周期性振动，其余横摇、纵摇、升沉和首摇都在约初始的100 s 以内达到相对平衡。因此对于浮吊来说，在作业工况下，水平面上的纵横荡为其主要的运动方式，并呈现周期性大幅度的震荡现象。其中，纵荡在迎浪（0°）和随浪（180°）的两个浪向工况下出现较大幅度的纵荡位移，且呈现一定周期的重复性，在-2.4～0.5 m范围反复震荡，周期约500 s。纵荡在横浪及斜浪（45°/135°）呈现正弦波式规则振动，振幅约2 m。横荡在横浪（90°）情况出现大幅横荡位移，且呈现周期性，在-0.8～3.2 m 反复震荡，周期约500 s。

图11 首摇时域响应图

3 结 论

操作中应该注意合理利用浪向施工，尽量使船舶处以斜浪工况。在对应浪向下，船舶运动最终处于相对平衡状态，且振荡幅度小，对纵横荡都有较好的抑制，利于吊装作业；同时应注意规避危险浪向（如迎浪、随浪和横浪），在这些工况下，纵荡和横荡处于周期性位移振荡过程。

作业过程中如果无法完全避开危险工况，则应实时监控船舶水平位移，避开位移变化较快的时间段，利用位移波峰或波谷的时间段（如本例中的200 s 和400 s 左右，见图12）。图13 显示在位移波峰波谷时间正是位移变化的的极小值情况，应该在此时间段完成最后的定位和吊装。

图12 90°横浪，横荡位移响应

图13 90°横浪，横荡速度响应

考虑到水平面的位移振荡为主要运动方式，为使船舶定位更准确，可采取增加系泊力的方式，进一步限制船舶位移。比如本船在现有系泊力基础上增加50%，同时系泊力阻尼系数也随之增大，则最后纵荡位移（图14）和横荡位移（下页图15）的振幅均明显减小，更利于吊装作业。

图14 纵荡位移响应

图15 横荡位移响应

本文的结论也同样适用于类似的靠锚泊定位的工程船舶，比如铺管船、全回转起重船等，比如在风浪流作用下，横荡和纵荡是最为明显的运动，应该在安全性和功能性设计上充分地考虑水平位移可能带来的风险。另外，最为有效的限制水平位移的方法，是增加系泊缆强度，施加更大的系泊力。