电网阻抗适应型船舶并网逆变器谐波抑制策略研究
刘 渊 陈 涛 傅晓红 夏 骏
(中国船舶及海洋工程设计研究院 上海200011)
引 言
根据国际油轮船东协会的研究报告,目前航运业每年约消耗20 亿桶燃油,排放超过12 亿吨的CO2,约占全球总排放量的6%[1]。为有效控制碳排放,基于能源效率与CO2联系的紧密性,IMO设立了EEDI 标准,EEDI 就是船舶消耗的能量换算成CO2排量和船舶有效能量换算成CO2排量的比例指数[2]。EEDI 指数越高,能源效率越低[3-4]。可再生能源的引入能有效降低EEDI 指数,为此,可再生能源在船舶上的应用引起越来越多的关注[5-19]。可再生能源通过并网逆变器与电网连接,并网逆变器通常采用PWM 调制方式,输出电流带有大量PWM 谐波。为避免PWM 谐波进入电网,干扰电网正常运行,需要在逆变器与电网间加入滤波器。近年来,LCL 及LLCL 等高阶滤波器备受关注[20-22],其能大幅降低滤波电感使用。高阶滤波器的谐振环节会在系统中引入谐振,常用的谐振抑制策略包括无源阻尼[20-21]和有源阻尼策略[22-23]。文献[20]提出的无源阻尼策略能有效抑制船舶光伏逆变器的谐振尖峰并加强谐波衰减能力。文献[22]采用逆变器侧电感电压前馈的有源阻尼方式抑制高阶滤波器谐振,能有效保证系统稳定。针对船舶电网,开展电网阻抗适应型船舶并网逆变器谐波抑制策略研究,对船舶电网的谐波抑制以及安全稳定运行具有较大意义。
图1 为船用多逆变器并联系统,多台逆变器通过变压器连接在公共耦合端PCC。

图1 船用多逆变器并联系统
文献[24]中指出,当有多台逆变器并联在公共耦合端,对于每台逆变器来说,它们的等效电网阻抗会大幅增大。等效电网阻抗的变化会导致基于高阶滤波器并网逆变器系统谐振峰偏移,从而使设计的阻尼方式失效。基于等效船舶电网参数变化,本文将以LCL 滤波器为例,针对船舶电网特点,提出一种电网阻抗适应型船舶光伏并网逆变器谐波抑制策略,并确保在等效电网阻抗变化时,单相并网逆变器系统的稳定性及谐波抑制的有效性。
1 理论基础
1.1 基于LCL滤波器的单相并网逆变器建模
图2 是采用网侧电流反馈的基于LCL 滤波器单相并网逆变器系统图,图3 为采用网侧电流反馈的基于LCL 滤波器单相并网逆变器控制框图。其中:Ginν是逆变器增益,其值为逆变器直流输入电压Udc与三角载波幅值Utri之比;L1为滤波器逆变器侧电感;L2为逆变器网侧电感;Lg为电网等效电感;Cf为滤波器电容;电网基波频率fo= 50 Hz。
根据梅森公式,可以得到并网逆变器入网电流与逆变器输出电压的开环传递函数式(1)。


图2 基于LCL滤波器单相并网逆变器系统图

图3 基于LCL滤波器单相并网逆变器控制框图
可以看出,滤波器的谐振频率如式(2)所示。

1.2 电网参数变化分析
逆变器至变压器的电缆等效阻抗ZT为变压器短路阻抗;ZC2为变压器至PCC 的等效电缆电抗;ZG为发电机等效电抗;ig1-ign为逆变器输出电流;igN为N台逆变器总并网电流;ug1-ugn为逆变器并网电流;Ug为发电机电压。

图4 多逆变器并联系统模型
此处假设逆变器全部相同,即

当逆变器全部并网运行时,

当单台逆变器并网运行时,

由此可见,对于单台并网逆变器,电网等效阻抗在多逆变器并联时,会发生大范围的变化。当ZC1远小于ZT+ZC2+ZG,N台逆变器并网运行时,对于单台逆变器的等效电网阻抗为单台运行时的N倍。电网阻抗主要包括变压器短路阻抗Zg、线路阻抗ZC1、ZC2以及发电机阻抗Zs。
假设有20 台2 kW/220 V/50 Hz 的逆变器,总功率为40 kW,各自通过50 m 的电缆并联在变压器上,变压器通过100 m 电缆连接至400 kW 船用柴油发电机。电网阻抗按下述方法选取:
(1)考虑容量裕度,选择变压器额定功率SNT= 50 kVA,短路电抗标幺值xdT″=2.9%,忽略电阻,短路阻抗2π/ 50 = 0.089 mH;
(2)发电机额定功率SNG= 400 kW,短路电抗标幺值xdG″= 0.12,短路阻抗= 0.12×4002/ 400 / 2π/ 50 = 0.15 mH (发电机选取0.12短路电抗);
(3)线路阻抗在本文中当作纯电感考虑。线路阻抗包含逆变器至变压器段以及变压器至发电机两段,PCC 端至发电机电缆较短,此处忽略。根据电流大小,逆变器至变压器段选择2.5 mm2的电缆,线路的电抗0.102 mΩ/m,该段线路的阻抗ZC1= 50×0.102 / 2π/ 50 = 0.016 mH,变压器至发电机段选用95 mm2,线路的电抗0.0809 mΩ/m。电缆阻抗ZC2=100×0.0809 / 2π/ 50 = 0.026 mH。
最小的电网电感Lgmin选为 0 mH,此处认为逆变器离网运行模式下取最小电感。当所有的并联逆变器都工作时,可以得到最大的电网电感Lgmax= 0.016 +(0.089 + 0.15 + 0.026)×20 = 5.316 mH。
图5 为电网等效阻抗变化时Gui-ig伯德图,可以看出,LCL 滤波器会在系统中引入谐振,影响系统稳定性,需要采用谐振抑制策略抑制谐振。
等效电网阻抗大范围变化时,LCL 谐振峰出现了大范围的变化,这将导致常用的谐振抑制策略失效。因此,以LCL 滤波器为例,本文提出一种电网阻抗适应型船舶并网逆变器谐波抑制策略,在电网阻抗大范围变化时,并网逆变器系统能保持稳定。

图5 电网等效阻抗变化时Gig-ui伯德图
2 电网阻抗适应型船舶并网逆变器谐波抑制策略设计
基于上述分析,以LCL 滤波器为例,本文提出了一种电网阻抗适应型船舶并网逆变器谐波抑制策略,能在电网参数变化时,保证基于LCL 滤波器并网逆变器的大范围稳定性。
此处,选定单相逆变器为研究对象,额定输出功率为Prated= 2 kW,逆变器直流输入母线电压为Udc= 350 V,电网电压Ug= 220 V,开关频率为fs= 20 kHz,基波频率为fo= 50 Hz。
2.1 逆变器侧电感L1设计
逆变器侧电感L1的选择取决于电感电流纹波,通常选取15%~30%的额定电流,本文选定20%为设计标准。此处,设定额定输出电压为Ug,额定输出电流峰值为Iref,逆变器侧电感电流纹波为ΔIripple。单相逆变器采用单极性正弦脉宽调制(SPWM)时,电感电流纹波与滤波电感有如下关系[25]:

式中:d表示占空比。当占空比d= 1/2 时,电感L1的下限值为:

根据现有参数,此处选择逆变器侧电感L1= 1.8 mH。
2.2 滤波电容Cf 的设计
滤波电容Cf的选择决定逆变器产生的无功功率大小,这里限定逆变器产生的无功功率小于5%额定功率:

根据现有参数,此处选择逆变器滤波电容Cf= 2μF。
2.3 网侧滤波电感L2的设计
对于LCL 型滤波器而言,L2的选取原则取决于开关频率附近的并网电流谐波低于0.3%,由于L1和Cf已经确定,L2的计算可以依据公式(6)得到[21]:
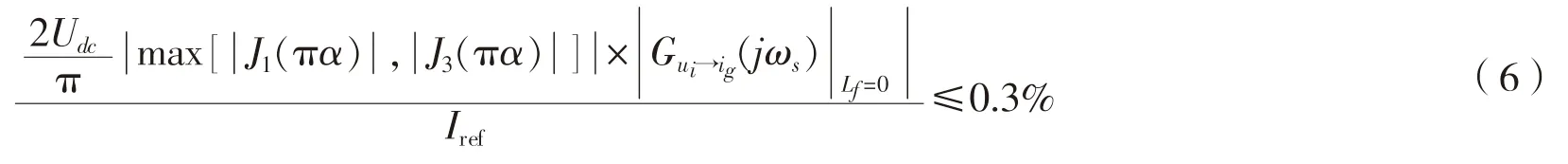
式中:J1( πα)和J(3πα)分别表示对应于开关频率的1、3 次边频带谐波的贝塞尔函数。

由式(7)可以看出,滤波器总电感量的增大有助于抑制入网谐波。因此保证谐波质量,只需要保证电网电感最小时,入网谐波最小。根据现有参数,此处选择电网侧滤波电感L2=1.8 mH。
2.4 阻尼设计
文献[26]指出,滤波器电容两端并联Rd-Cd的无源阻尼方式产生的阻尼功率损耗最小,因此本文选用并联Rd-Cd的无源阻尼方式,其拓扑结构如图6 所示。

图6 电容端并联 Rd -Cd 的无源阻尼方式
文献[21]提出, LCL 型滤波器的Rd-Cd无源阻尼方案的约束条件如式(8)所示。
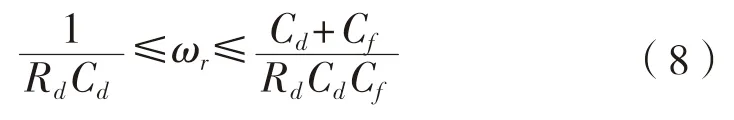
式中:ωr表示滤波器的谐振频率。当阻尼电阻由0 Ω 到∞Ω 变化时,ωr可近似为
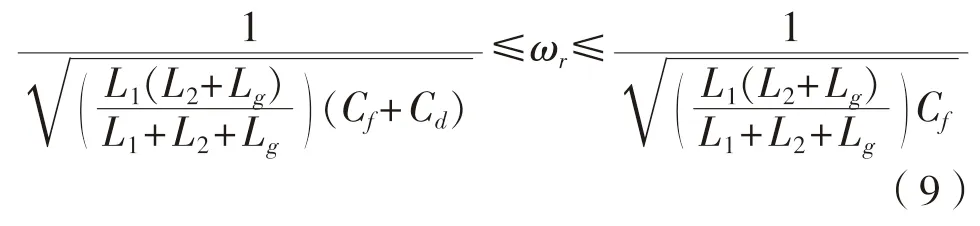
于是,阻尼参数Rd的选取依据为

f d可以简化为

将设计好的参数代入上式,求出阻尼Rd的取值范围为37.9 Ω ≤Rd≤42.4 Ω。若计算结果显示Rd无有效区间,则返回重新设计L2。因此,最后确定的LCL 无源阻尼方案所增加的Rd-Cd支路的参数为 :Rd= 40 Ω,Cd= 2µF。
2.5 控制器设计
采用电容两端并联Rd-Cd的无源阻尼方式的基于LCL 滤波器单相并网逆变器开环传递函数如式(12)所示。

其中,局部系统传递函数如式(13)所示。

为抑制低次谐波,本文选择PR+HC控制方式,PR+HC控制器的传递函数如下:

其中Kih为各2h-1 次谐振补偿的增益,ω0是电网角频率。在穿越频率fc之后,PR控制器可以简化为Kp[27]。fc_plant是局部系统的相位穿越-180°的频率。
为保证系统的稳定性以及鲁棒性,在电网电感最大及最小时,系统相位裕度GM应大于0 dB,相位裕度PM应大于45°。系统幅值裕度及相位裕度分别为式(15)及(16)。

为保证系统的动态性能,系统带宽应尽可能大,此处选择Kp= 0.85,Kih= 7。电网电感最大时,带宽为371 Hz。此时系统开环传递函数伯德图如图7 所示。
图8 为Kp= 0.85 时电网等效阻抗变化时开环系统幅值裕度与相位裕度,可以看出,系统在电网等效阻抗变化时保持稳定。下页图9 为设计流程图。
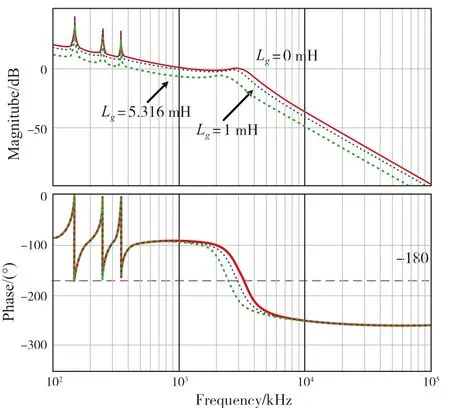
图7 电网等效阻抗变化时开环系统Gopen-loop伯德图
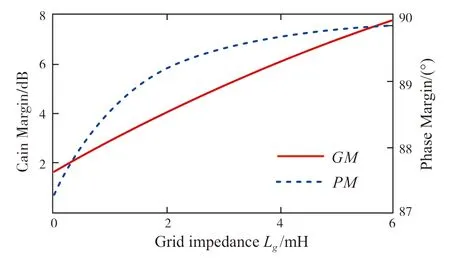
图8 电网等效阻抗变化时开环系统幅值裕度与相位裕度
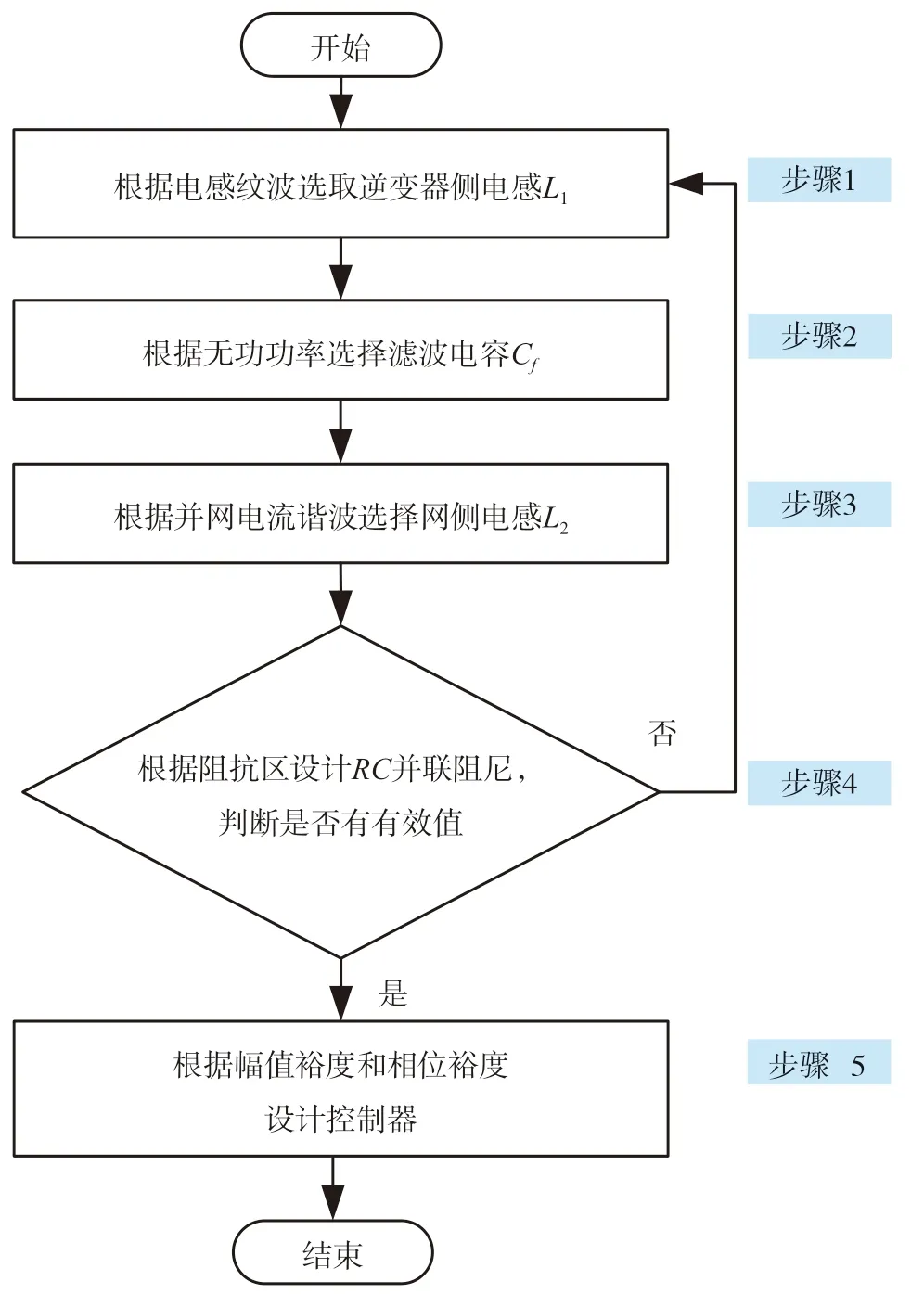
图9 设计流程图
3 仿真验证
本文选用PSIM 仿真软件,基于上文的计算分析,搭建了系统仿真平台。
图10 为Lg= 5.316 mH 时 基于LCL滤波器单相并网逆变器入网电流,THD= 0.06%;图11 为Lg= 0 mH 基于LCL 滤波器单相并网逆变器入网电流,THD= 0.26%。可以看出:入网电流在电网电感大范围变化时系统稳定,且入网电流THD 值小,谐波抑制有效。
中国船级社(CCS)规定,船舶电网暂态电压波动允许±20%。本文在Lg= 5.316 mH 时,t= 0.3 s时增大20%并网电压,图12 为Lg= 5.316 mH 时,单相并网逆变器入网电流波形ig及电网电压ug。可以看出,一个周期内入网电流恢复稳定,系统动态性能良好。

图10 基于LCL滤波器单相并网逆变器入网电流Lg = 5.316 mH THD = 0.06%
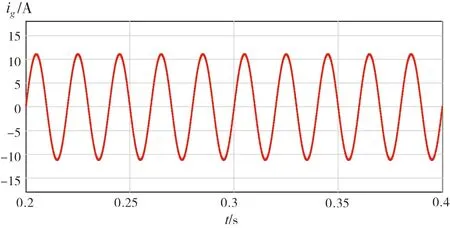
图11 基于LCL滤波器单相并网逆变器入网电流Lg = 0 mH THD = 0.26%

图12 Lg = 5.316 mH时单相并网逆变器入网电流波形及电网电压ug(t = 0.3 s ug增大20%)
4 结 语
本文以船舶并网逆变器系统为例,分析了船用并网逆变器系统等效电网阻抗的大范围变化特征;结合LCL 滤波器性能指标以及阻抗区的概念,设计了并联RC 阻尼的LCL 滤波器结构,并给出了具体设计流程。仿真结果显示,本文所提出的设计方法可以有效抑制逆变器所产生的谐波,并维持基于LCL 滤波器的船舶并网逆变器系统在等效电网阻抗大范围变化时的稳定性。

