基于变密度法的VLCC 货舱内横向强框架拓扑优化研究

朱俊侠 吴嘉蒙

（中国船舶及海洋工程设计研究院 上海200011）

引 言

结构优化是近些年来船舶设计领域研究的热点，主要的优化目标是尽可能地减轻结构质量，约束条件是保证船体结构强度，最终实现船体结构轻量化设计。目前船舶结构优化技术主要集中在尺寸优化和形状优化，而拓扑优化方法的应用研究还不够深入。作为结构创新设计领域的一项重要技术，拓扑优化能够在满足设计要求的前提下，寻求结构传递载荷的最佳路径以及承受载荷的最佳结构型式，而这正是常规优化手段难以做到的。

在船舶结构设计中，拓扑优化方法多应用于肘板、型材等局部结构的构型优化，这些优化对象的构型较简单、尺寸规模较小，优化效果有限。货舱是油船的主要组成部分，其中货舱内横向强框架存在一定的优化空间，若对其应用拓扑优化技术可获得一定的减重效果。而目前国内外针对整个货舱结构的拓扑优化研究还不多见，其主要原因在于缺少实用化的舱段结构拓扑优化设计技术［1］。

因此，本文将以VLCC 某档横向强框架作为优化对象，在三舱段模型中开展复杂工况下结构拓扑优化设计研究：针对协调版油船散货船共同结构规范（以下简称新CSR 或CSR-H）计算工况复杂繁多的问题，给出了一套工况筛选方法，通过该方法不仅可以确定影响拓扑构型的重要工况，还能够评估其权重系数；探讨了拓扑优化时设计域范围、约束条件等方面的内容；开展基于新CSR 的VLCC横向强框架多工况拓扑优化计算。

1 基于SIMP 的变密度拓扑优化法相关理论及强框架拓扑优化流程

拓扑优化是一个｛0，1｝问题，即结构材料的“有”与“无”问题。由于无法将结构设计区域中的每个参数都作为设计变量，故可采用有限元法将结构进行离散处理。然而离散问题在数学上较难处理，通常将此问题转化为连续问题去研究［2］。变密度法通过人为的引入“单元密度”这一概念，建立了“单元密度”与结构材料的弹性模量E 之间的某种函数关系，优化时以材料单元密度为设计变量，在0～1 之间连续取值，其中0 和1 分别代表该单元应完全删除和保留，以此将结构拓扑优化问题转换为材料的最优分布问题。

固体各向同性惩罚微结构模型（SIMP）是变密度法中最常见的插值模型之一。SIMP 法通过引入惩罚因子p对单元密度进行有限度的惩罚，以尽量减少中间密度单元的数目，使结构单元密度尽可能趋于0 或1。在优化前和优化后的材料弹性模量之间引入如下关系式［3］：

为数值求解稳定，通常令Emin=E0/1 000。当Emin取值远小于E0时，Emin可以忽略不计。则上式可简化为：

式中：p>1，为惩罚因子；E0为实际材料的杨氏模量；xi为单元密度。

基于变密度的拓扑优化方法在实际工程中的应用较为广泛，具有较好的数值稳定性及准确性。本文多工况下VLCC 货舱内横向强框结构的拓扑优化是在HyperWorks/OptiStruct 软件平台上完成的。基于HyperWorks/OptiStruct 软件平台的横向强框架拓扑优化设计流程如图1 所示。

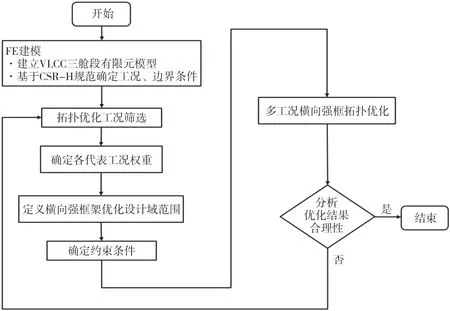
图1 横向强框架多工况拓扑优化的流程图

2 VLCC 三舱段初始模型及拓扑优化对象

2.1 VLCC三舱段结构有限元模型

作为研究对象的该型VLCC 的主要参数为：垂线间长327.00 m、船宽60.00 m、型深29.80 m、结构吃水21.50 m、载重量308 000 t。

根据设计图纸采用MSC/PATRAN 软件建立该VLCC 三舱段结构有限元模型，通过中国船级社的HCSR-DSA 工具，生成新CSR 规范中用于舱段结构强度评估的载荷工况及边界条件；随后再将生成的bdf 文件导入HyperWorks/OptiSruct 中，建立了包括计算载荷在内的三舱段结构拓扑优化的研究对象。初始的VLCC 三舱段模型如图2 所示。

图2 VLCC三舱段模型

三舱段结构有限元模型采用笛卡尔坐标系，X轴沿船长方向，向船首为正；Y轴沿船宽方向，向左舷为正；Z轴沿型深方向，向上为正。板材采用四边形和少量三角形板壳单元模拟，骨材采用梁单元模拟。有限元网格大小为纵骨间距×肋距。船体材料包括高强度钢（HT32 和HT36）和低碳普通钢，材料弹性模量为206 GPa，密度为7 850 kg/m3，泊松比为0.3。

2.2 VLCC舱段结构拓扑优化构件定义

船舶结构为典型的板梁组合结构。水密舱室的空间划分是基于船舶的功能性要求，因此水密构件无法作为拓扑优化对象［4］；按照简化工艺的要求，强框间距和纵骨间距通常取值固定，不作为拓扑优化的宏观优化对象［1］；纵骨等已有相关学者［5-6］采用简化载荷在局部子模型中进行了拓扑优化，但对于舱段整体结构性能的影响较小，因此本次研究中不对纵骨等局部纵向构件进行拓扑优化。

横向强框架作为货舱区域内的主要支撑构件，主要承受局部支撑构件传递过来的载荷。由于油船货舱内的横向强框架数量较多、分布较广，且其结构质量在整个货舱区域占比较大，可以影响其他结构的应变能分布，故对其开展拓扑优化能够较大幅度地改善整个货舱区的应力分布状态。因此，本文选择的拓扑优化对象为VLCC 货舱内横向强框架。

本文旨在研究基于变密度法的VLCC 横向强框架拓扑优化方法，为提高优化效率，研究对象仅针对三舱段中间货舱内FR77 肋位的横向强框架，其他的横向强框架暂保持初始设计状态不进行优化。FR77 档横向强框架的初始有限元模型如图3 所示。

图3 拓扑优化的目标横向强框架

3 拓扑优化工况筛选及权重确定

为使拓扑优化结果更具实用性，本文拓扑优化研究中的载荷工况采用新CSR 中规定的——两道油密舱壁型油船中间货舱区有限元强度评估所要求的载荷工况。拓扑优化计算时舱段有限元模型的端部边界条件也是根据该规范中的相关规定进行设置。

多数文献在研究船舶结构拓扑优化时，采用的工况相对简单，没有考虑实船设计时船级社规范要求的复杂工况；而基于不同工况的拓扑优化结果差异巨大。经研究发现：

（1）在优化计算中纳入所有的工况可能得不到合理的横向强框架拓扑构型，如新CSR 中舱段结构强度校核的工况多达四十多种，不同工况下对应着不同的最优结构构型，但同时考虑太多工况可能无法得到强框的主要载荷传递路径；

（2）舱段直接强度评估的耗时较长，而舱段级结构拓扑优化需要多次迭代，计算耗时会更长，因此考虑的工况数量太多会使计算的效率急剧降低；

（3）经计算发现并非所有工况都对货舱内横向强框结构型式有较大影响，忽略部分影响较小的工况可能对最终的优化构型几乎没有影响；

（4）船级社舱段直接强度评估的计算工况中，有些属于极端工况、有些属于常用营运工况，极端工况下的最佳载荷传递路径与常用营运工况下的最佳载荷传递路径往往不同，如何综合分配极端工况和常用工况的影响权重值得研究。

因此，需要筛选出若干个对强框结构影响较大的代表性工况，同时通过权重系数平衡常用工况和极端工况，基于筛选出的拓扑优化计算工况来获得横向强框架的拓朴构型。最终的拓扑构型工程化之后，船体结构要在规范规定的所有直接强度计算工况条件下进行强度校核。

3.1 拓扑优化工况筛选

为筛选出对横向强框架影响较大的工况，判断每种工况对强框架的“影响程度”及“决定单元数量”，本文将基于初始舱段结构的强度评估结果，分别以各个工况下单元的最大屈服利用因子max_UF与每个工况的决定单元数量OCC作为考核指标。上述两个指标在MSC/NASTRAN 软件中可通过以下方式计算得到：

（1）基于新CSR，分别计算各工况下横向强框架各单元的等效应力（Von Mises）、屈服利用因子及最大屈服利用因子max_UF；

（2）强框的每个单元在诸多工况下会存在一个最大屈服利用因子max_UF，其对应的工况可认为是该单元的决定工况，随后分别统计每个工况的“决定单元数量”OCC。

基于以上筛选原则，分别计算了FR77 档横向强框架各有限元单元在42 种工况下的最大屈服利用因子max_UF 与决定单元数量OCC，具体如表1所示。

表1 新CSR中各工况的最大屈服利用因子max_UF与决定单元数量OCC

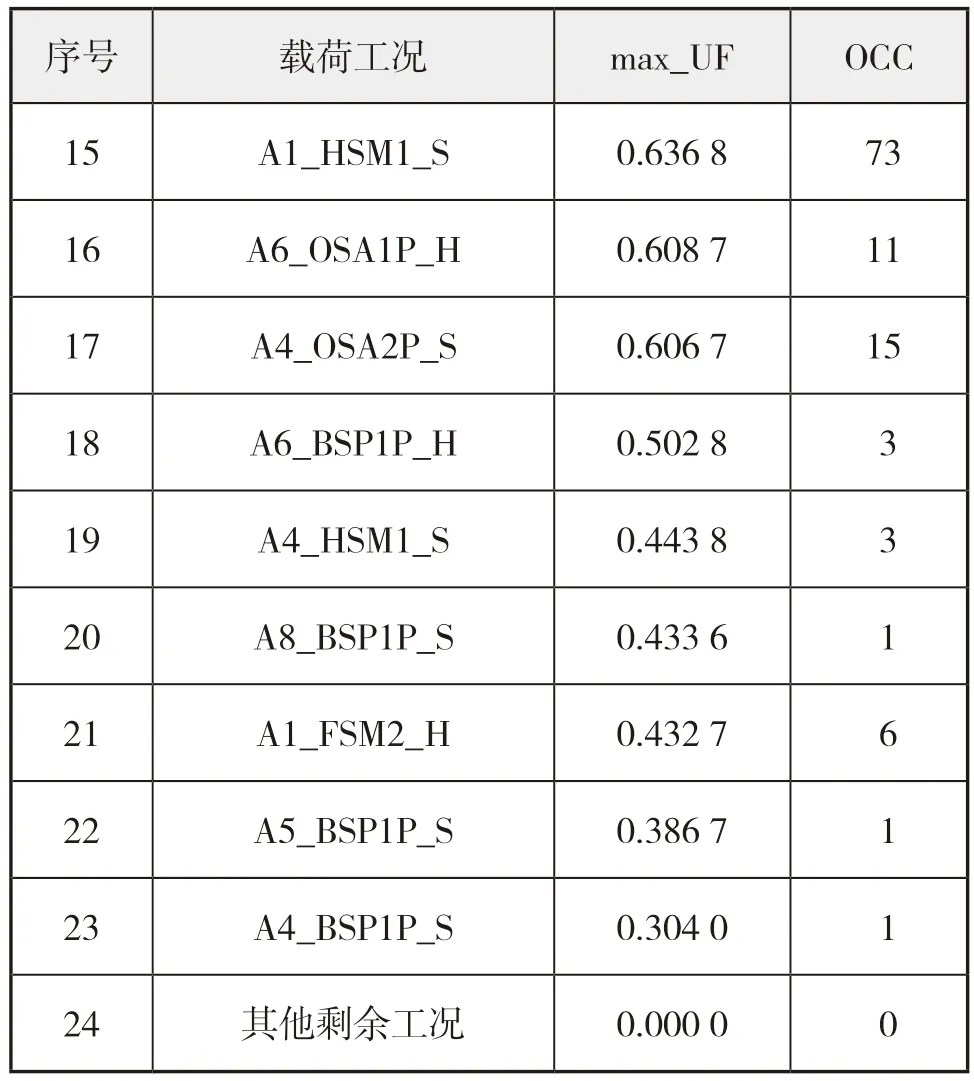
续表1

分别将上述两种指标数值从大到小进行排序，优先选取两种指标都比较大的工况，舍弃决定单元数量OCC 太少的工况，在综合考虑装载模式因素后，最终挑选了15 种工况，在表2 中根据装载模式进行罗列。

表2 新CSR工况筛选结果

3.2 优化工况权重确定

多工况优化时，各工况权重对最终优化结果具有重要意义。目前各工况的权重系数往往是有经验的工程师统筹多方面的因素后自主确定的，这种方式对工程师的经验提出了巨大的挑战。同时，大多数研究在确定各工况权重时，仅仅考虑了工况本身的恶劣程度因素，认为工况越恶劣，其对应的权重也就越大。然而在VLCC 实际营运中，极端工况并非经常出现，反而是一些非恶劣工况具有较大的出现概率，因此对于拓扑优化而言，寻找常用工况下最优的承载传力路径会更有意义，对于提高船舶的结构强度和使用寿命更有价值。对于极端工况，只需满足规范要求的强度衡准即可。本文认为在各工况权重设定的方法中，应当在考虑工况恶劣程度因素的同时考虑工况在日常营运出现的概率，如此所得的工况权重系数才更加准确。另外，从结构强度角度考虑时，不能只关注某工况下结构的最大应力值，还要关注该工况下的“决定单元数量”。

基于上述考虑，针对筛选得到的15 种工况，分别以单元最大屈服利用因子max_UF、工况下结构的决定单元数量OCC 以及营运出现概率三种考核指标进行重要性排序。对于最大屈服利用因子max_UF、工况下结构的决定单元数量OCC 这两种考核指标，各工况的对应指标数值如本文表1 所示，考核指标数值越大，所对应的工况重要性权重也越大，反之亦然。至于各工况的出现概率，认为VLCC 在实际运营过程中，满载或空载所对应航行工况以及港口内装卸货物所对应的工况较为常见，这些工况可用A1、A2、A8、A9、A10、A11、A12、A14 装载模式下的工况进行近似代替，赋予这些工况较大的相同权重，而剩下的工况则认为出现的概率较小，故赋予较小的权重。三种考核指标下各工况重要性权重分配情况如表3 所示。

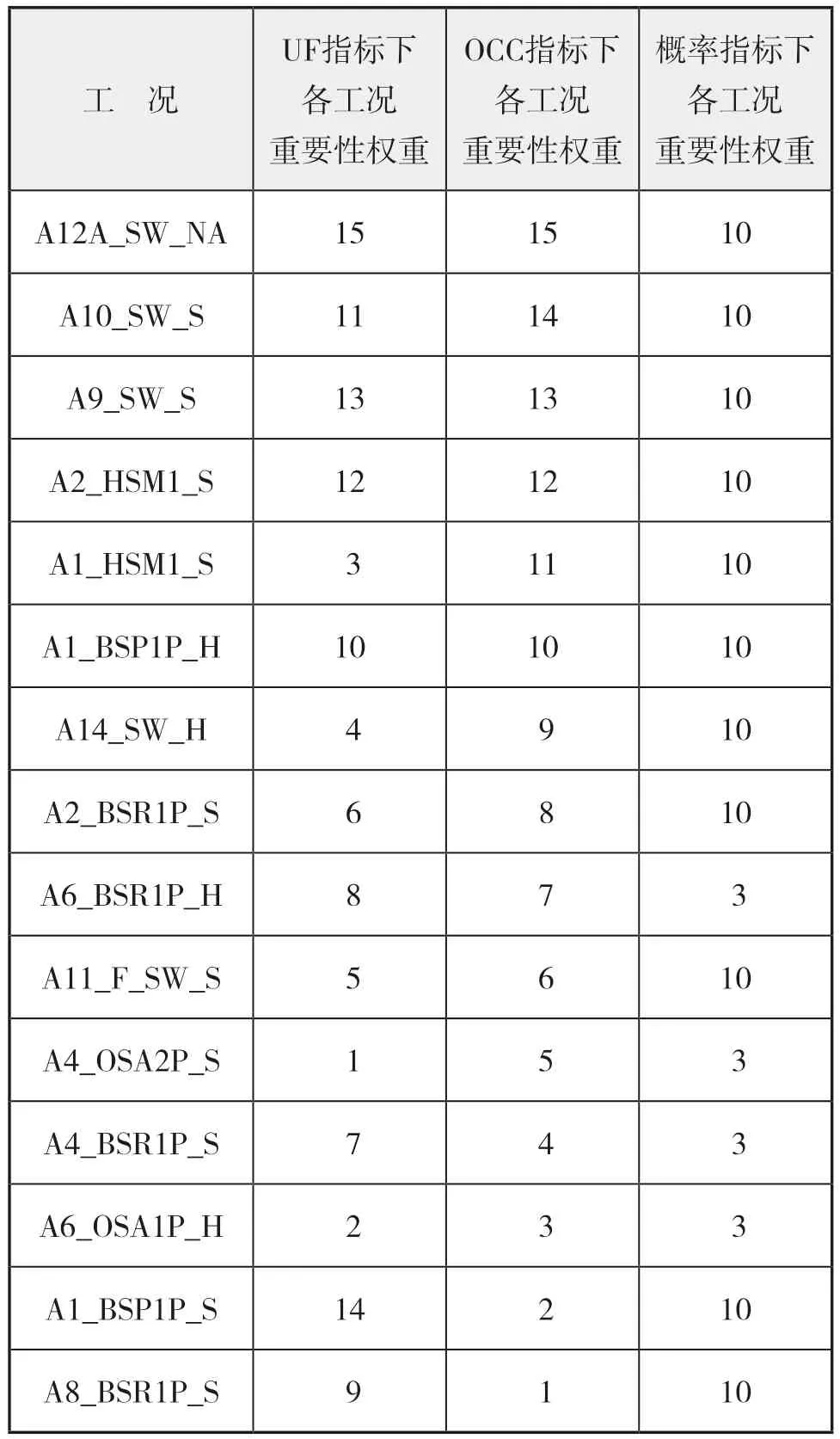
表3 三种指标下各工况重要性权重分配情况

为了统筹三种指标下各工况的权重，通过线性加权法将三种指标下的权重进行叠加，进而得到各工况综合权重系数。max_UF、OCC 与营运出现概率三种指标的线性权重比例设为0.15 ： 0.15 ： 0.7， 该 比 例 可 根 据 不 同 设 计 人 员 的 经验进行调整。由此得到了各工况的综合权重系数，具体如表4 所示。

表4 各工况的综合权重分配情况

4 VLCC 货舱内横向强框架多工况拓扑优化研究

4.1 设计域范围确定

舱段级别的船体结构拓扑优化不同于机械三维实体零件，其单元基础还是二维板壳单元，可以认为是由多个二维设计域组合在一起的拓扑优化设计。在传统的有限元计算中，主要支撑构件的腹板是以壳体单元体现的，而面板用杆单元或者梁单元来模拟，主要支撑构件腹板上的屈曲加强筋也用杆单元或者梁单元来模拟。但是针对横向强框架的拓扑优化，优化设计域的单元类型应该统一采用二维板壳单元，否则拓扑优化计算的工作量根本不是普通计算机所能承受的。邱伟强等［1］曾尝试在二维壳单元的中间混杂一维杆单元，用来模拟主要支撑构件的面板和腹板加强筋，但未成功，所以认为二维壳单元混杂一维杆单元一起作为拓扑设计域在目前阶段是不可行的。

拓扑设计域的范围应该包含优化对象所有可能出现的型式，对于货舱内横向强框架而言，理论上其所在平面在货舱范围内皆可作为设计域。但是，在新CSR 中对甲板强横梁、纵舱壁垂直桁的最小腹板高度都有规定，而且横向强框架的腹板作为纵向骨材的支撑需要保持一定的腹板高度，因此这部分结构是必然存在的。基于上述原则，本文在拓扑优化设计中为纵舱壁垂直桁腹板、甲板强横梁初步设置了一定高度的非设计域（纵舱壁垂直桁最小腹板高度为2 100 mm，甲板强横梁最小腹板高度为890 mm），将原始设计中强框架所在平面的其他区域全部用二维壳体单元进行密闭填充来作为拓扑优化设计域，如图4 中黄色区域所示。

图4 横向强框架拓扑优化设计域所在剖面

4.2 约束条件确定

拓扑优化中常用的约束条件包括应力、位移及体积分数等约束。体积分数约束可通过约束优化后设计域内有效结构的体积或者体积分数，以此来实现轻量化设计。新CSR 在舱段结构强度校核时只考虑单元应力衡准，而船体结构变形方面的约束条件隐含在屈曲强度衡准中，因此在结构设计时只要满足规范中的结构屈服和屈曲强度衡准即可。由于目前拓扑优化方法中暂时无法考虑板格屈曲问题，因此基于整体和局部屈曲特性的横向强框架优化尚无法进行。

经计算研究发现，设计域板厚与结构应力大小密切相关，并会产生较大影响，而目前横向强框架拓扑优化设计域的板厚尚无确定性方法来获得，因此过早引入应力约束不仅意义不大，而且可能影响横向强框架最佳拓扑优化构型的出现。本文通过拓扑优化技术，旨在寻找横向强框架的最佳承载型式，以体积分数作为约束条件，刚度最大化作为优化目标即可达到该优化目的。横向强框架的结构设计需要经历多个阶段，拓扑优化的结果主要是作为其概念性设计的一种构型参考，在此基础上设计的结构如果不满足规范的应力要求，还可以在详细设计阶段通过尺寸优化、形状优化等措施来实现。

关于是否加入应力约束这一问题，除上述分析外，本文还进行了若干工况的试算。优化工况为A1_HSM1_S、A2_HSM1_S、A9_SW_S 三 种 工 况，分别给与不同的应力约束情况。具体应力约束情况与优化结果如下页表5 -表7 所示。

由上述优化结果发现，对于横向强框架的拓扑优化，在施加设计域单元应力约束时，不同应力值约束下得到的拓扑构型有时差异较大，甚至可能得到无法满足制造工艺要求的拓扑构型；而无应力约束，仅施加体积分数约束时，常常能够得到清晰的载荷传递路径。同时，无应力约束所得到的横向强框架拓扑构型与存在应力约束时所得的构型相比，往往具有较大的刚度，而且设计域内单元应力的最大值也较小，这些正是横向强框架在结构设计所想要得到的。通过上述试算结果与分析可认为，横向强框架在拓扑优化时，无应力约束的优化设置往往能够获得较为理想的拓扑构型。

船舶结构设计不仅包括前期概念设计阶段，还包括了详细设计阶段。拓扑优化本身属于概念设计阶段，此时很多结构参数尚无法确定，因此没有必要也无法约束过多响应，只要寻找出结构的最佳载荷传递路径即可。综上所述，本文认为在横向强框架拓扑优化时，约束条件应不设置应力约束，仅设置体积分数约束。

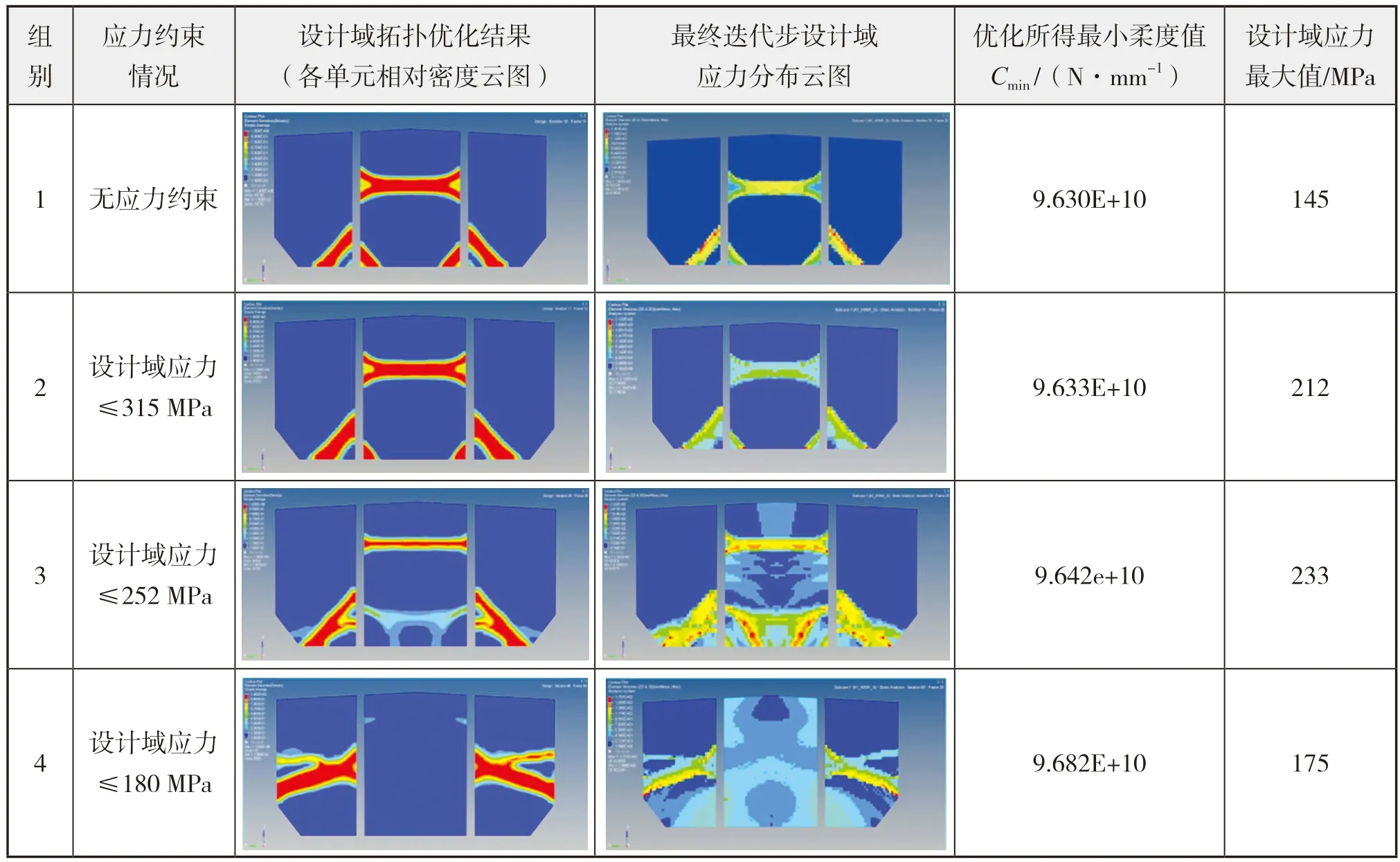
表5 A1_HSM1_S工况下多种应力约束情况优化结果

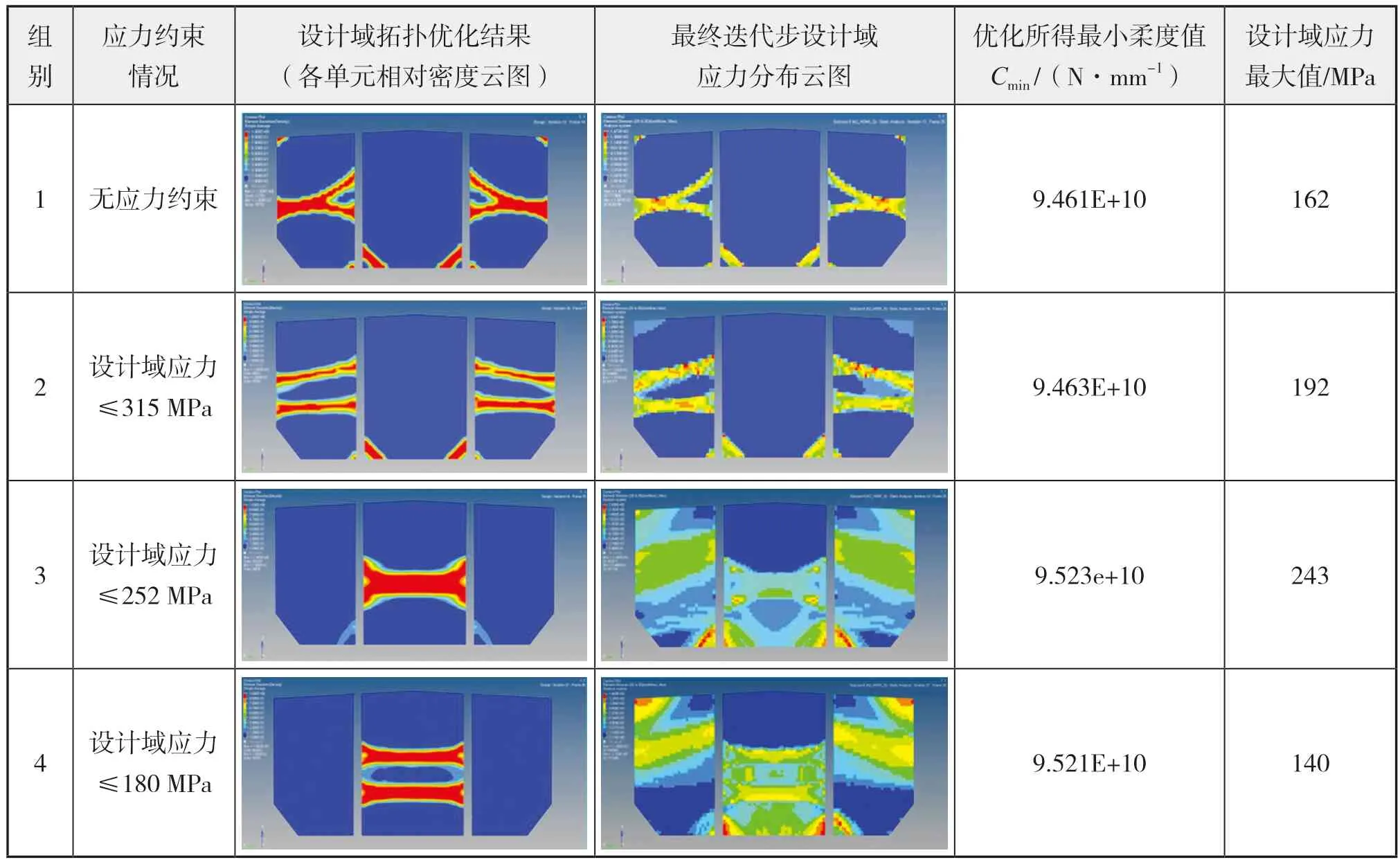
表6 A2_HSM1_S工况下多种应力约束情况优化结果

表7 A9_SW_S工况下多种应力约束情况优化结果

4.3 多工况下VLCC横向强框架拓扑优化

在进行多工况下的横向强框架拓扑优化时，设计域板厚通过初始强框架与框架上屈曲加强筋及面板的等效体积来确定，取为23 mm。约束条件仅包括体积分数约束。多工况下VLCC 货舱内横向强框架拓扑优化的数学模型可描述为：

在HyperWorks/OptiStruct 中进行优化设置，目标函数值经过多步迭代后达到收敛，最终得到多工况下VLCC 货舱内横向强框结构的优化结果，设计域内各单元的相对密度分布如图5 所示。多工况下横向强框架的最终优化构型如下页图6 所示。

图5 最终迭代步设计域内各单元相对密度分布情况

图6 横向强框架最终拓扑优化结果

通过优化结果可知，多工况下横向强框架最优的结构型式为：在中间舱布置撑杆，在纵舱壁底部两边分别设置斜撑与肘板。由于规范中上甲板的载荷较小，拓扑结果显示在设计域上端区域不存在主要传力路径，因此无主要结构出现。

本文优化所得的强框架拓扑构型与初始设计十分相似，是目前横向强框架最为常见的一种布置型式，具有较好的结构刚度与布置特性。由此可认为，将上述拓扑优化方法应用于三舱段横向强框架的拓扑优化设计是可行与有效的。由于该拓扑构型是通过优化算法计算得到的，其结果具有合理性和可靠性，可为现有强框结构的设计提供一种构型参考。

5 结 语

本文基于变密度法的结构拓扑优化理论及HyperWorks/OptiStruct 优化软件平台，以VLCC 货舱横向强框结构刚度最大化为优化目标，依据新CSR 分析计算，克服了VLCC 舱段结构拓扑优化计算工况多、工况权重系数难以确定等困难，最终给出了可付诸工程实际应用的VLCC 货舱内横向强框架拓扑构型。

在进行优化工况筛选时，本文提出了一套工况筛选方法，采用该方法既可筛选得到各代表工况，还可获得其权重系数。通过该方法，可以有效减少优化设计时对工程师经验的依赖，进而获得较为可靠的权重系数。针对横向强框架的几何结构特性，通过理论分析后认为在约束条件中应不设置应力约束，仅通过设置体积分数约束来达到优化目的。通过合理的优化结果可认为，本文所提出的优化思路与方法应用于VLCC 三舱段横向强框架的拓扑优化设计是完全可行与有效的，优化结果可为横向强框架的构型优化提供借鉴，而且该优化思路可应用于其他船型结构的优化设计中。