限制水域船体水动力计算分析与自由面数值阻尼的应用
王伟飞 彭亚康 濮 骏 赵晓斌 杨震峰
(中国船舶及海洋工程设计研究院 上海200011)
引 言
浮体在限制水域的运动计算具有很多的工程用途(如船在河流或航道中的运动等),目前商业软件HydroStar 提供此项功能,但在此功能下无法引入自由面数值阻尼。池壁格林函数的计算一直是浮体在限制水域运动计算的一个重点问题,Newman[1]讨论了浮体在航道和水池中以定常速度航行下的水动力计算问题,其采用了无界流假定,池壁格林函数由1/r关于池壁的无穷个镜像叠加得到,此方法无法应用于自由面问题。C.M. Linton[2]导出了一种新的满足自由面条件、基于有限水深池壁格林函数的表达形式,但其表达方式与目前常用的开敞水域格林函数的形式差别很大,需要重新编制算法,且其收敛性依赖部分系数,实施起来并不方便。目前较为流行的做法为通过将无穷个开敞水域自由面格林函数关于池壁进行镜像叠加[3-5],该方法可充分利用现有的开敞水域格林函数计算法,但需要计算一个收敛较慢的无穷级数求和问题。对于无穷级数求和,可以采用一些加速的办法[6],但也无法满足本文中计算的要求。Xia Jinzhu[3-4]和Chen-Xiaobo[5]采取了对池壁格林函数的分区域计算方法克服了收敛慢的问题,本文在此基础上采用渐近法,进一步分析了其奇异性,从中分离出了奇异项,并对剩余项进行切比雪夫逼近,实现了池壁格林函数的高效和高精度计算。
线性势流理论水动力计算无法计入粘性和非线性效应,导致在计算部分问题时会出现数值共振问题从而引起计算结果失真。为处理这一问题,可在势流方法中引入人工数值耗散项[7],即数值阻尼来解决。本文将自由面数值阻尼引入限制水域的浮体运动计算,并通过自由面积分的解析解较好地解决了这一问题。本文的所有计算均通过Fortran编程计算求解。
1 控制方程和定解条件
根据三维线性势流理论,在一宽度为b,深为h 的航道中,浮体以频率ω和时间因子e-iωt作周期性运动;记源点坐标为(ξ,η,ζ),场点坐标为(x,y,z),池壁格林函数G满足的定解条件如下[3-4]:

式中:g 为重力加速度。满足上述定解条件的解为:

式(5)等号右侧为开敞有限水深自由面格林函数的无穷级数(m为整数),其表达式为:
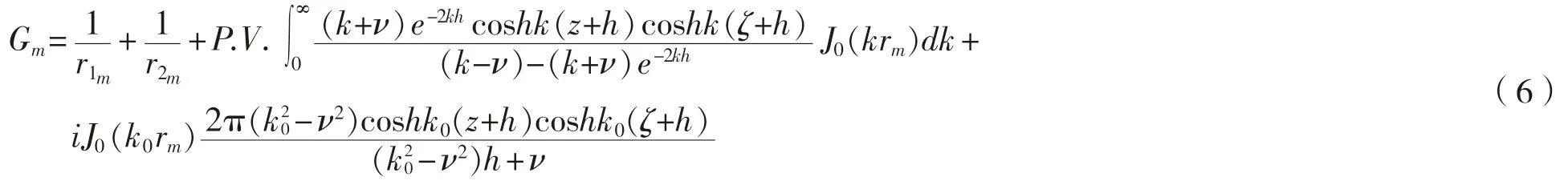
Gm的级数表达式为:
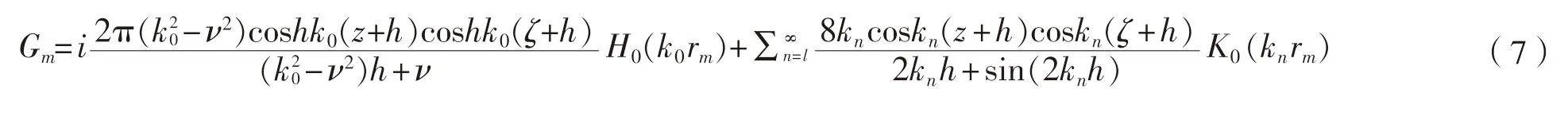

(6)式和(7)式中:J0为0 阶第一类贝塞尔函数;
K0为0 阶修正的贝塞尔函数;
H0为0 阶汉克尔函数。
2 自由面池壁格林函数计算
由式(5)可知,池壁格林函数可通过有限水深自由面格林函数展开的无穷级数得到。但是由于式(5)级数收敛非常慢,直接进行求和计算的成本非常高,实际工程应用中几乎是不可行的,所以需要找到高效的数值方法进行计算。
为提高计算效率,并保证计算精度,将式(5)分为3 部分[3-5],即,
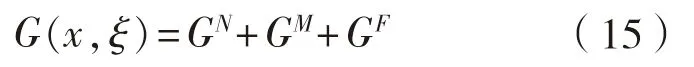
式中:包括近场部分GN,中场部分GM和远场部分GF。近场采用级数直接求和的方法:

中场部分利用式(7),并注意到修正的贝塞尔函数渐近表达式为

式(16)中项数M0和式(17)中项数M1的取法在文献[3-4]中已有详细论述,在此不再赘述。利用Graf’s 加法公式[6]和汉克尔函数的渐近展开近似[6],可得 :

式中:

er为剩余偏差项;
B=k0b,表示无因次化的航道宽度,系数
3 数值方法与切比雪夫多项式逼近
Newman[8]给出了近场部分GN的详细计算方法,其中为了提高计算效率,对近场部分进行了切比雪夫多项式逼近,中场部分GM计算较简单,可通过级数求和以及有理分式逼近或直接采用现有的函数库来求解,以上计算方法无需赘述。本节主要介绍远场GF的高效计算方法以及对其进行切比雪夫多项式逼近方法。
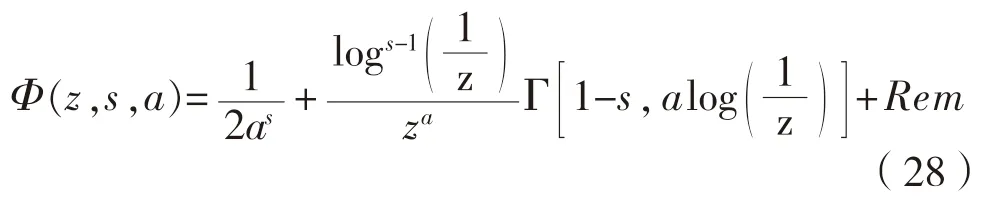

其中,剩余项的渐近表达式LerExtract(z,s,a)的奇异性与Φ(z,s,a)一致,所以原函数减去奇异项之后的剩余项可通过多变量切比雪夫多项式来逼近:
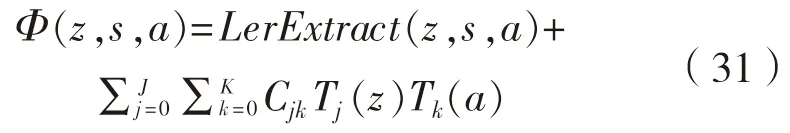
式中:Cjk为逼近多项式的系数;Tj和Tk分别是关于z和a的切比雪夫多项式;截断项数J和K根据不同的区域来选取,通常可通过试算确定。
为更好说明式(31), 现取s=1/2,a=2/3,b∈(0,π/2)分别对Φ(z,s,a)、LerExtract(z,s,a)、Φ(z,s,a)-LerExtract(z,s,a)作图,对应下页图1-图3。可以看出:Φ(z,s,a)和LerExtract(z,s,a)在b= 0 处存在奇异性,剩余项不再存在奇异性,且为光滑函数,可用切比雪夫多项式高效地逼近。

图1 Φ(2bi,1/2,3/2),b∈(0,π/2)曲线

图2 LerExtract(2bi,1/2,3/2),b∈(0,π/2)曲线

图3 Φ(2bi,1/2,3/2)-LerExtract(2bi,1/2,3/2),b∈(0,π/2)曲线
4 自由面人工数值阻尼施加
由于势流理论无法计入粘性效应等因素,采用池壁格林函数求解浮体运动时在某些特定的频率会产生数值共振,造成计算结果与实际情况有较大的差异。为了较好地处理数值计算所带来的奇异性问题,可通过引入人工数值耗散项来解决。通常的做法是在自由面条件中引入数值阻尼ε[7]。
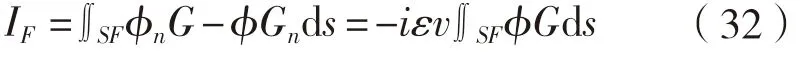
当场点在自由面上时,积分方程为:
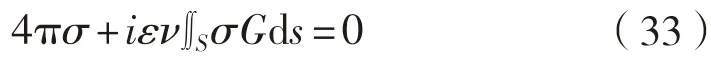
式中:σ为源强;G和Gn分别用池壁格林函数及其法向导数代入。由于池壁格林函数在自由面上存在奇异性,为保证计算精度,需要小心处理。可通过去奇点法进行数值积分计算,即积分核中先减去一奇异项,此奇异项的积分可给出解析表达式。阻尼系数ε取一小值,通常可通过试算和试验方法确定。
5 算例与比较分析
为验证池壁格林函数计算和本文方法的准确性,通过算例进行对比验证。算例为计算一直立圆柱(见图4)在方形航道中的水动力系数,航道宽100 m、水深50 m、圆柱半径为15 m、圆柱吃水为40 m。将水动力系数计算结果与BV 船级社的HydroStar 软件的结果进行比较,此项比较计算中不增加自由面数值阻尼(Hydrostar 的池壁格林函数计算无法考虑自由面数值阻尼)。

图4 算例圆柱体示意图(含自由面数值阻尼面元)
附加质量和阻尼系数的计算结果如图5-图14所示(图中标记“hstar”为HydroStar 的计算结果;“my”为本文的计算结果,水动力系数进行了无因次化处理。ρ为流体密度,V为圆柱排水体积,d为圆柱直径)。由于在势流理论下圆柱艏摇的附加质量和阻尼系数为0,所以结果中不包含艏摇模态。
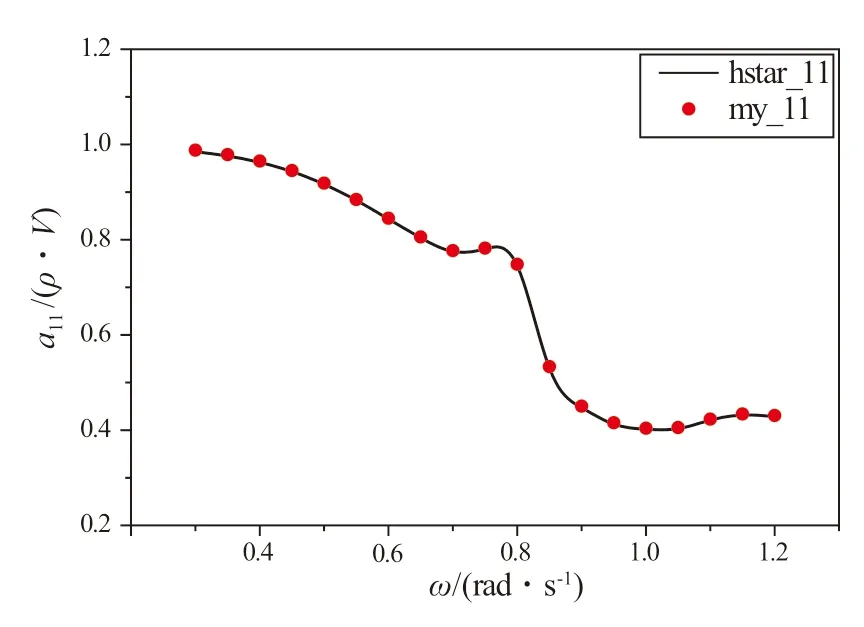
图5 纵荡附加质量
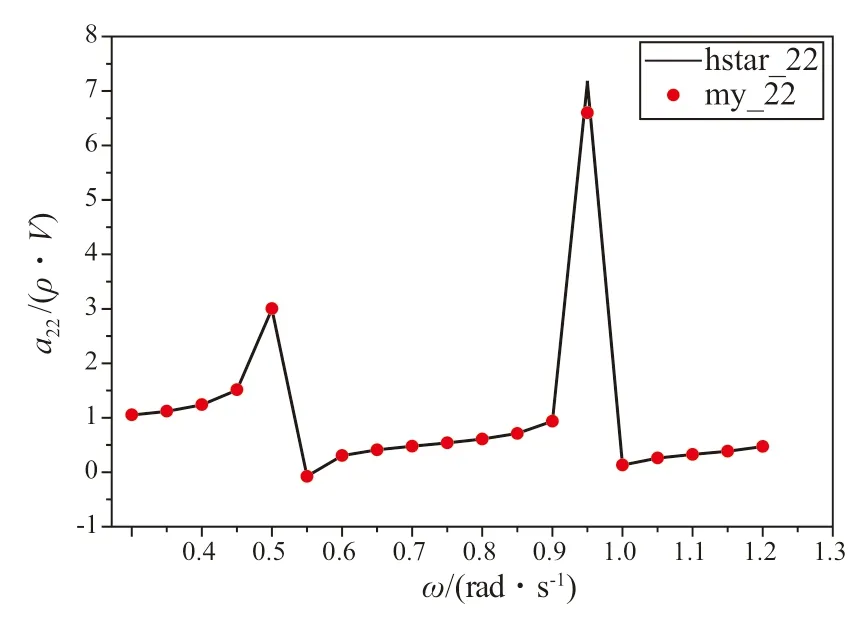
图6 横荡附加质量
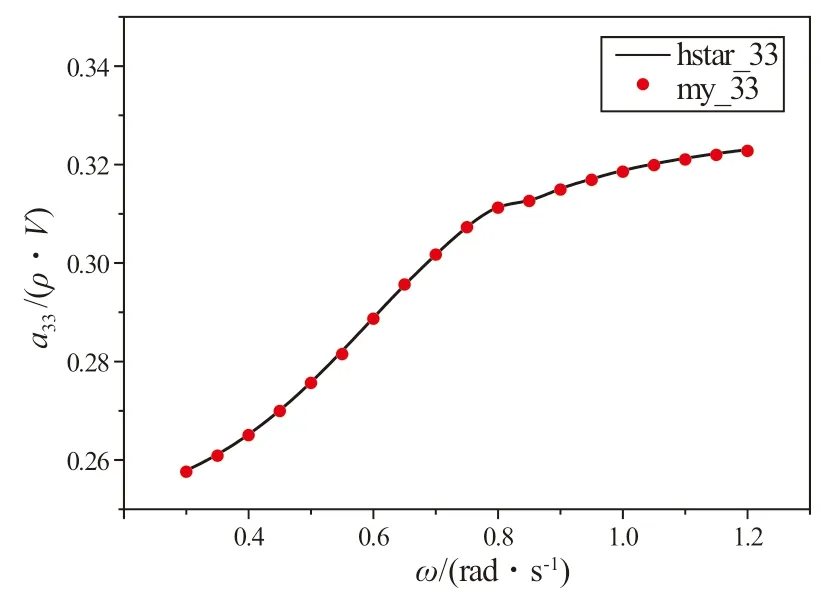
图7 垂荡附加质量

图8 横摇附加质量
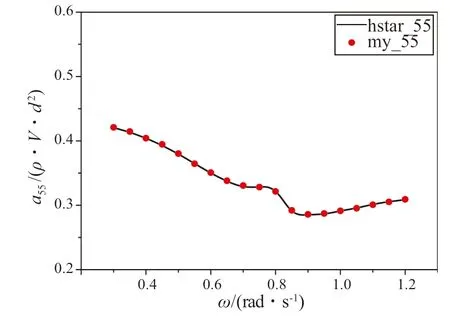
图9 纵摇附加质量

图10 纵荡阻尼系数

图11 横荡阻尼系数

图12 垂荡阻尼系数

图13 横摇阻尼系数

图14 纵摇阻尼系数
从结果可以看出,本文的计算结果和HydroStar的计算结果非常吻合,验证了本文计算方法的可靠性和计算精度,特别是池壁格林函数计算的准确性。结果中的横荡和横摇曲线中出现了明显的数值共振的频率点,此共振现象是由于基于势流理论的池壁效应造成的。
本文通过引入自由面数值阻尼来消除数值共振点,为验证自由面数值阻尼的有效性,本文根据算例来进行验证。在图4 所示的计算模型下(数值阻尼层的尺寸为96 m(横向)×60 m(纵向),数值阻尼系数ε= 0.5),考虑自由面数值阻尼之后的水动力系数计算对比结果如图15~图16 所示。图中标记为TGF 的曲线为没有考虑自由面数值阻尼的池壁效应计算结果;标记为TGF_damp_rec 的曲线为考虑自由面数值阻尼的池壁效应计算结果;标记为FG_Opensea 的曲线为在普通开敞水域自由面格林函数下的水动力系数计算结果。文中没有列出阻尼系数的比较结果,计算表明,在引入人工数值阻尼之后,阻尼系数对数值阻尼系数ε较为敏感,后续将继续研究如何合理地确定数值阻尼系数的大小。

图15 横荡附加质量
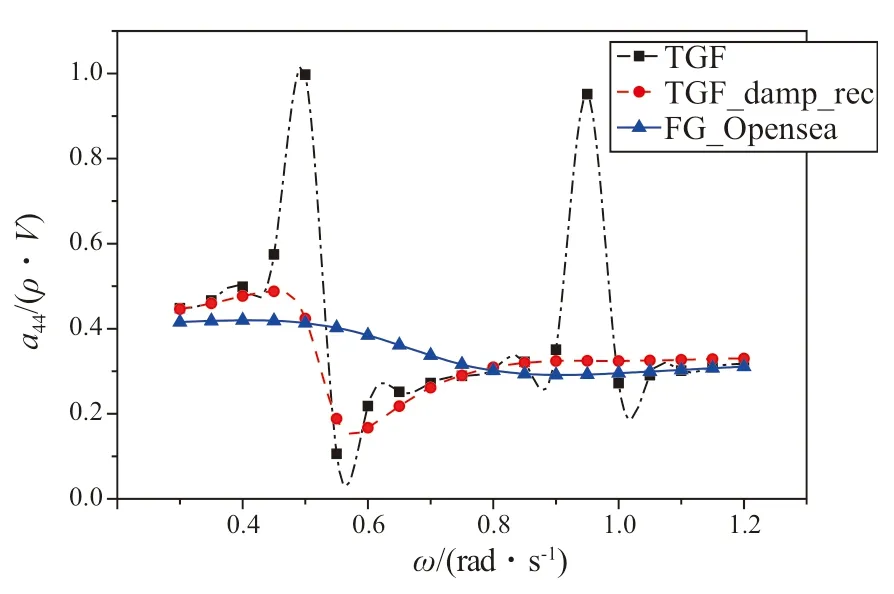
图16 横摇附加质量
从结果中可以看出,施加了自由面数值阻尼之后,附加质量系数随着频率变化是一条光滑的曲线,严重的数值共振现象不再出现,奇异性问题得到了较好的解决。从而使计算结果更为合理,与实际情况也更为吻合。
6 结 语
本文利用自由面池壁格林函数来考虑池壁效应,对其进行了基于切比雪夫多项式逼近的高效和高精度计算,并通过自由面数值阻尼来解决计算中出现的数值共振问题,目前公开商业软件尚不具备此项功能。本文方法为浮体在限制水域的运动等响应计算提供了一个更为合理的方法,具备较大的工程应用价值。下一步的工作将着重解决如何确定数值阻尼的大小,使计算更便捷、结果更合理。

