双边界限定下的运动目标跟踪方法*
邓 豪, 刘桂华, 杨 康, 包 川, 邓 磊
(西南科技大学 信息工程学院,四川 绵阳 621010)
0 引 言
由于存在目标表观变化、遮挡问题、周边环境的干扰和光照变化等诸多因素的影响,目前还不存在性能优良的通用目标跟踪算法,而根据不同应用需求衍生了不同跟踪算法[1~7]。但多数在短时间跟踪上表现良好,长时间鲁棒性不足。Adam A等人[8]用多个图像块来表示目标借以进行滑动搜索表决目标,但由于图像块是固定放置的,而不能对旋转或者有粘连性的目标进行跟踪。Hua G等人[9]提出了基于马尔科夫网络的基于部分目标跟踪的方法,检测出不一致的部分目标,这种方法对遮挡、背景杂乱和目标变形有较好的鲁棒,但由于图像的描述以及马尔科夫网络,导致其连续跟踪效果差。Grabner M等人[10]提出一种用自适应分类器的方法匹配关键点进行跟踪,当前图像帧中目标的可信关键点用来训练样本并更新分类器,但其对于分类器的训练需要大量的正负样本,对环境的适应性差。Hare S等人[11]提出一种与Grabner的方法相似的目标跟踪算法,给每个关键点赋权重,并在一个统一结构性输出的学习框架中更新这些权值,但对于非平面的目标,这类方法的对应性估计并不好。
一种目标跟踪算法的重要功能是:能够在任何时间都可以在目标被遮挡、目标在视野中消失等情况下,避免再次手动初始化,进行快速强鲁棒地找出图像中的目标。应用最为广泛的是无任何先验知识的无模型跟踪方法,跟踪器唯一知道的就是视频序列中第一帧的信息,然后利用第一帧初始信息在后续的视频帧中对目标在图像中的位置进行估计。其优点在于不需要任何先验知识或训练学习,因而可广泛应用在不同场合。但无模型跟踪对于目标跟踪领域目标遮挡、背景杂乱、光照变化等挑战性情况还是没有很好地解决。
本文提出一种双边界限定下的运动目标跟踪算法。图像帧的关键点可以通过匹配和跟踪相结合的方法得到,并将两种方法得到的关键点进行融合。其次是利用一致性约束来确定目标的中心位置、当前图像帧中目标相对于第一帧图像的旋转角度与尺度变化。最后利用双边界限定解决尺度变化中边界关键点残缺、初始化目标区域背景点对长时间跟踪的影响。
1 算法设计与实现
1.1 关键点跟踪、匹配及初步融合
在给定视频序列I1,…,In,图像帧I1中给定初始目标区域b1,在后续视频序列的每一图像帧中,确定感兴趣的语义目标的位置、姿态,或判定其丢失(图像帧中不可见),即确定目标在图像帧中的位置b2,…,bn。
在视频序列第一帧中,在初始化条件I1及b1下,建立关键点集模板如下
(1)
每个关键点标记一个坐标点r∈R2和一个描述符f,为了跟踪过程中计算简便,本文采用二元描述符f∈{0,1}d。在I1中,将初始化O的关键点位置均值归一化。在第t(t≥2)帧图像目标识别与跟踪时,对应关键点的描述如下
(2)
式中α为图像中对应关键点的位置,m为当前关键点对应关键点集O的索引。
本文采用金字塔光流[12]进行视频帧的目标跟踪,通过计算前向光流和后向光流的欧氏距离,将两次光流距离相差大于阈值的点予以排除,得到关键点集T。其图像约束方程为
I(x,y,z,t)=I(x+Δx,y+Δy,z+Δz,t+Δt)
(3)
在第t(t≥2)帧图像It中,利用FAST及BRISK方法得到的关键点集P为
(4)
每一个关键点与第一帧关键点集O进行K最近邻(K-nearest neighbor,KNN)匹配,取K值为2,即每个匹配返回两个最近邻描述符。对P中每一个关键点计算其描述符和在第一帧的关键点描述符的汉明距离,并将满足以下条件之一的关键点去除:
1)匹配到了背景关键点,则将该关键点从前景关键点更新至背景关键点;2)最佳匹配的汉明距离大于阈值;3)最大匹配与次佳匹配的匹配距离之比大于阈值。采用这种方法,实时更新关键点集O中前景特征点P_fg与背景特征点P_bg,并确保识别到的关键点与关键点集O具有良好匹配,增加了跟踪算法的鲁棒性。
对于跟踪及匹配到的关键点集T和M,由于存在计算差异等问题,两个关键点集并不完全一样,被跟踪目标同一关键点在两个关键点集中有着不同的表示,故将关键点集T与M进行融合,两个关键点集合并为大小为NKt的关键点描述集Kt,并删除其中重复冗余的关键点,得到融合后特征点描述集K′。理论看来,匹配到的关键点的鲁棒性更好,因为其并不依赖于对运动目标的运动估计。
1.2 表 决
为了便于描述,将图像中目标的运动归一化为相机静止,目标运动。目标在运动过程中,尤其是背景也在随着目标发生变化的运动过程中,因为目标在图像中尺度与角度的变化,导致跟踪效果鲁棒性急速下降。
在第t(t≥2)帧图像It中,进行目标的识别与跟踪重点是获取到目标中心在当前图像帧中的位置,故使K′的每个关键点(a,m)都对目标中心h(a,m)→R2进行表决,即
(5)
目标在仅发生平向运动情况下,目标中心可表示为
hT(a,m)=a-rm
(6)
式中rm为关键点集O中相应关键点的相对位置。当目标在移动过程中引起目标在图像中尺度变化时,式(5)及式(6)并不能很好地得到目标的中心,这时引入尺度因子S。于是式(6)可写为
hS(a,m)=a-S*rm
(7)

S=med‖Kdi,j‖/‖Odi,j‖,i≠j
(8)
目标在运动过程中在图像上必不可少地会产生旋转,则上述投票方法鲁棒性很低,在式(7)上加入旋转因子,有
hR(a,m)=a-S*R*rm
(9)
式中R为一个二维旋转矩阵,其表示如下

(10)
图像中两点相对于归零化极轴的角度如图1所示。图1(a)表示在第一帧图像I1中关键点i与关键点j相对于极轴所成角度,图1(b)表示在第t(t≥2)帧图像It中,关键点i与关键点j相对于极轴所成角度,由图可得Δαi,j=α1(i,j)-αt(i,j)=90°。其中,αi,j可以通过反正切求得。
在第一帧及第t(t≥2)帧图像中分别求特征点集O及特征描述集K′的角度集Oαi,j(i≠j)及Kαi,j(i≠j),并利用中值方法增强系统的鲁棒性,旋转因子Δα可表述为
Δα=med{Kαi,j-Oαi,j,i≠j}
(11)
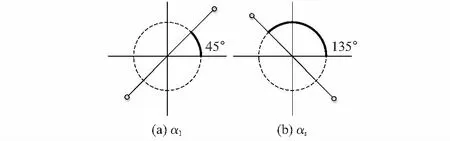
图1 目标运动过程中角度变化示意
1.3 一致性约束
在跟踪过程中,无论坐标α还是索引m出错,都会导致表决结果错误,指向图像中随机位置。故在特征描述集K′确认目标位置前,通过对关键点的一致性约束来确认和移除异常关键点,通过层次凝聚方法[13]对特征点集V聚类,核心思想是基于欧氏距离测量的差异度量,在聚类过程中,数据根据一个相似度矩阵被组织成层次结构,形成一个树状表示,并通过阈值δ进行剪枝。从V1,V2,…,Vn多个聚类结果中选取最大的类V_max,该类中关键点集作为目标的有效描述,并去除其他类的关键点。这种方法减少了对目标的是否只能平面移动的限制,并允许关键点从初始位置有少许漂移,增强跟踪系统的鲁棒性。
层次聚类过程中,其计算量较大,若特征点集V的元素过多,对系统资源消耗过大,会造成跟踪系统实时性指数性下降,并间接影响跟踪系统的鲁棒性。故设定特征点集元素阈值τ(经验值250),在超过阈值时,利用压缩感知中的正交匹配追踪(orthogonal matching pursuit,OMP)算法[14,15]对V进行压缩传感。稀疏度γ为
(12)
式中 |V|为特征点集V的元素个数,「⎤为向上取整,由式(12)确保V的元素个数不大于τ。
由于目标在运动过程中不可避免会出现遮挡、从视野丢失、正常跟踪等多种情况,故在由一致性约束从V中得到最大的类V_max后,V_max元素的个数很大程度上能反映出目标的跟随状态,设定ε1(经验值0.15)、ε2(经验值0.55)分别为目标丢失、遮挡的阈值,其具体含义为:
|Vmax|<ε1|O|:目标丢失;
ε1|O|≤|Vmax|≤ε2|O|:遮挡;
ε2|O|<|Vmax|≤τ:正常跟踪。
目标在运动过程中从视野丢失(图像帧中不可见),则令其目标框为丢失前目标框,并在整个图像帧中逐步扩大,直到图像边界。目标被遮挡或正常跟踪过程中,利用上述方法得到目标的有效描述集V_max,并利用中值公式得到目标的中心μ,再利用上述求得的目标尺度因子和旋转因子可得到目标的大小及旋转角度,以确定目标在当前图像帧中的位置。
1.4 双边界限定
一致性约束下目标跟踪过程中目标在缩放以及旋转过程中,不可避免会丢失掉外邻边界的关键点以及边界上部分关键点,而这部分关键点被更新到背景点集中后,对当前以及之后的跟踪鲁棒性存在负影响。且在手动初始化目标时,不可避免会在目标区域存在部分背景关键点,这一部分关键点作为初始前景关键点集中元素,后续图像帧中关键点与其进行匹配会引起极大的误差,且对尺度因子、旋转因子的计算产生影响,进而降低整个跟踪系统的鲁棒性。
为了解决上述问题,引入双边界对一致性约束予以限定。在保证Δα计算方法不变的情况下,将式(8)尺度因子S进行扩张为S′,扩张程度由ξ(0≤ξ≤0.2,经验值0.08)限制。则式(8)改写为
S′=(1+ξ)med‖Kdi,j‖/‖Odi,j‖,i≠j
(13)
将扩张后边界内以及边界上所有点作为特征描述集V′,并利用同求取Δα的方法求取该特征描述集相对应旋转因子Δβ,在S′及Δβ的条件下进行特征描述集V′的一致性约束,得到关于目标的边界bx2,并将其作为bx1的约束边界。在目标被良好识别与跟踪情况下,目标边界bx1与约束边界bx2的中心应重合或其欧氏距离Δx在一定范围内;目标边界bx1与约束边界bx2相对角度Δθ应保持不变或在一定变化范围内。故设立距离变化阈值为x,角度变化阈值θ。当Δx>x时,缩小ξ直到Δx≤x,当Δθ>θ时,以bx2为基准,以第一帧目标边界与约束边界角度β1为变化量,确定目标边界bx1。
2 实验与结果分析
分别于室内及室外两种外部环境下对目标进行长时间连续跟踪,实验平台为Manifold嵌入式开发板,主频为2.2 GHz,RAM为2 GB DDR3。在跟踪过程中人为使目标被遮挡、脱离视野、旋转平移等,检测目标识别与跟踪系统鲁棒性。在两个场景下对目标各进行3 600帧图片序列跟踪,目标识别与跟踪系统具有极好的适应性,对于上述常见问题鲁棒性极好。
由于本文提出方法基于特征点检测与跟踪,特征点数目的多少在一定程度上反映出跟踪情况,实验过程中,跟踪过程中各观测点特征点个数如图2所示,可以看出跟踪系统在目标尺化、运动、旋转等情况下特征点保持相对平衡状态,而在目标被遮挡、丢失时,图像帧特征点相对会有剧烈变化。在目标被遮挡后恢复视野以及丢失后恢复视野可以避免再次手动化,对目标进行快速强鲁棒性跟踪处理。

图2 目标跟踪过程中观测点特征点数目

dt=
(14)
(15)
(16)
(17)
在已有实验平台上分别将该方法与CT[18],TLD[19]这两种目标跟踪经典算法进行对比,从各自的专题网站上获取源码,并按其最理想要求进行配置,其平均帧率(fps)、中心距离均值、重叠率实验结果为TLD帧率为10.44 fps,中心距离均值为6.7 px,重叠率为71 %;CT帧率为51.62 fps,中心距离均值为11.4 px,重叠率为47 %;本文方法帧率为13.68 fps,中心距离均值为4.4 px,重叠率为82 %。
相对于CT及TLD经典目标识别与跟踪算法,本文方法具有中心误差距离较小、重叠率较大的优点TLD因P-N学习机制,提高了跟踪系统重叠率,但因重检测及训练学习,导致帧率不高,实时性不好。CT基于压缩感知理论,实时性较高,但中心误差距离较大,重叠率较低。由于本文对一致性约束进行双边界限定,并进行两次聚类,计算量偏大,故其实时性逊于CT跟踪算法等。
但对于平均重叠度为50 %,以上分析不能区分只是视频的50 %表现完全精确还是整个视频表现不是很精确。在式(16)中用了一个阈值ω来将每帧分为真实的正样本(TP)和假的负样本(FN)。TP控制了每帧的精度要求。将ω赋值为25 %,50 %,75 %分布表明为低、中、高的精度,将recall[18]设为每帧的效果衡量值,即查全率,表明目标可见时有多少帧满足重叠度ω的要求。计算方法
recall=TP/(TP+FN)×100 %
(18)
将CT,TLD以及本文方法,分别在跟踪过程中计算查全率,具体为:低精度(ω≥0.25)时,CT为43 %,TLD为87 %,本文方法为92 %;中等精度(ω≥0.50)时,CT为28 %,TLD为55 %,本文方法为57 %;高精度(ω≥0.75)时,CT为17 %,TLD为19 %,本文方法为19 %。本文方法在低中高精度要求情况下取得了最佳结果,并分别领先第二名5 %,2 %,2 %的查全率。
3 结束语
本文提出了一种双边界限定下聚类一致性约束的目标识别与跟踪算法,不需要进行学习与训练,根据第一帧的初始化信息建立基本特征描述集,并在后续的跟踪识别过程中更新该特征描述集。目标在运动过程中,尺度相对于初始尺度在一定缩放比例下是确定的,关键点相对于归零化极轴的角度相对于初始角度是确定的,以及约束边界与目标边界的角度、中心点欧氏距离是一定的。本文充分利用这些初始条件,使跟踪算法具有在后续视频序列中,在目标被遮挡、视野丢失等多种情况下,避免再次手动初始化,进行强鲁棒性跟踪处理。

