基于三轴光电跟踪系统的目标捕获方法

陈德毅， 柳万胜， 贺 东， 祝培军

(1.中国科学院 光束控制重点实验室，四川 成都 610209； 2.中国科学院 光电技术研究所，四川 成都 610209；3.中国科学院大学，北京 100049)

0 引 言

光电跟踪系统具有高分辨率、高精度和抗电子干扰等特点，广泛应用于导弹制导、火炮控制、星体跟踪和靶场测量等方面，主要是对目标进行捕获、跟踪以及测量等工作。其中，捕获是跟踪、测量阶段的前提。

目前，国内外关于捕获方法的研究多针对两轴转台的光电跟踪系统。如，日本的LUCE系统就是典型的两轴转台的星地光通信平台，捕获阶段采用超前瞄准快反镜以缩短捕获时间，但系统结构复杂[1]；于思源等人[2]针对激光星间链路系统，捕获的目标相对光电系统属于低仰角目标；周彦平等人[3]分析了天基非合作目标捕获过程，但分析过程中对扫描区域只进行了简单的假设。

三轴光电跟踪系统由方位轴(A)、俯仰轴(E)、横倾轴(G)和视轴构成，系统结构简单且能很好地解决过顶跟踪问题。在实际的目标捕获跟踪中，当目标位于光电系统的天顶位置时，三轴光电跟踪系统将空间目标的运动速度分解到各轴上转动的角速度远小于两轴光电跟踪系统的分解结果，尤其是方位轴，使得三轴光电跟踪系统捕获跟踪目标时，视场内图像稳定，有利于目标的识别处理。由于结构的不同和在各轴上分解的速度不同，三轴光电跟踪系统的捕获策略不同于两轴，因此应重新考虑基于三轴光电跟踪系统的捕获策略，以缩短一定捕获概率要求下的平均捕获时间。本文针对这一问题进行了探讨，详细分析了捕获过程中扫描区域的特性以及设计扫描捕获方式的方法并给出了评价指标，最终建立了基于三轴光电跟踪系统的目标捕获方法，通过仿真实验验证了设计的捕获方法的有效性。

1 捕获方法原理

三轴光电跟踪系统受视场大小、探测性能的限制，在不确定区域内不能及时捕获目标。不确定区域(field of uncertain,FoU)是指某一确定的历元时刻，光电跟踪设备指向的位置，与目标在空间中的真实位置会存在一定的偏差，目标以一定的概率密度分布在该偏差所构成的区域内。为了短时间、高概率地捕获目标，需要三轴光电跟踪系统的各个轴相互配合，在FoU内设计出合理的扫描捕获方式。扫描捕获方式的设计与FoU的形状、大小以及目标在FoU内的概率分布类型有关，而FoU的这些特性又决定于引起FoU的一系列误差源。研究捕获方法的总体方案如图1。

图1 捕获方法的技术路线

2 捕获方法的建立

2.1 误差源分析

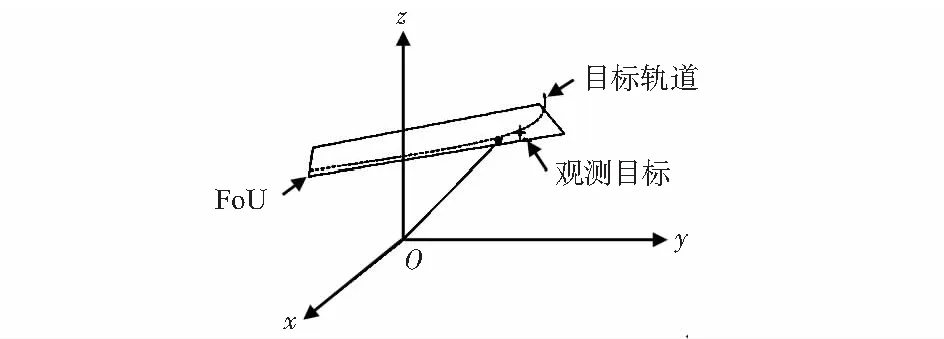
图2 目标在三轴测量坐标系中的位置

经分析引起FoU的误差源为：轨道预报误差、三轴指向误差、系统时间误差、测量站址误差。其中，主要误差为轨道预报误差和三轴指向误差；次要误差为系统时间误差和测量站址误差。

2.2 误差到FoU的映射

考虑主要误差到FoU的映射。首先讨论轨道预报误差，一般情况下，轨道预报采用点位预报，即给定(t,A,E,G)引导三轴光电跟踪系统对目标进行捕获跟踪。点位预报通常受轨道预报数、摄动力模型及参数的影响存在误差。针对中轨目标，设确定历元时刻，精密定轨提供的精确轨道数据为真值(t,Ar,Er,Gr)，为单站车载三轴光电跟踪设备提供的轨道数据为预报值(t,Am,Em,Gm)。轨道预报误差为

(1)

在多次测量的情况下，经分析得到，轨道预报值在方位和俯仰方向上存在随时间变化的系统误差和均值为μ,方差为σ的随机误差。假设提供的轨道预报数据很新，则可以认为随时间变化的系统误差已被修正。考虑轨道预报误差的随机误差，其在方位、俯仰方向上的概率密度函数(PDF)为

(2)

(3)

由于轨道预报误差中的随机误差在方位、俯仰方向上独立同分布，因此,μA0=μE0，σA0=σE0。为了得到轨道预报误差到三轴光电跟踪系统各轴上的分配情况，在方位轴A确定的情况下，误差传递关系如下[4]

(4)

式中i,j,k=0或1。

如图3给出了描述误差传递结果，可以看出，在方位、俯仰方向上服从高斯分布的轨道预报误差传递到三轴光电跟踪系统后，只有横倾轴G仍然服从高斯分布，设传递后的标准差为σEpre(mard,1mard为100 m处的10 cm)，σEpre(mard)。

图3 轨道预报误差传递到三轴的结果

根据三轴光电跟踪系统捕获高仰角目标的实际工作模式，三轴指向误差主要来自俯仰轴和横倾轴转角误差[5]，即

δE=f1(E,G)+f2(A,E,G)+εE

(5)

δG=g1(E,G)+g2(A,E,G)+εG

(6)

式中f1，f2，g1，g2为系统误差，εE,εG为随机误差。考虑修正三轴光电跟踪系统的系统误差之后，影响三轴指向的误差主要为系统残差和随机误差。文献[5]可知，在俯仰轴和横倾轴上误差分布为正态分布，其概率密度函数为

(7)

(8)

以上分析中，轨道预报误差和三轴指向误差是相互独立的。因此，根据误差合成原理[6]，误差合成后在俯仰轴、横倾轴的总标准差分别为

(9)

如图4所示为误差在俯仰、横倾轴上合成的结果。可以看出，合成后的误差在俯仰轴和横倾轴上的分布类型为高斯分布。

图4 主要误差合成的结果

现将三轴光电跟踪系统俯仰轴、横倾轴合成后的误差映射到空间FoU平面。连接视轴指向和轨道预报值的位置为直线L，作垂直L的平面O，垂足为坐标原点，沿轨迹的切线方向为方位轴，右手螺旋法则的方向为俯仰轴建立FoU所在平面的直角坐标系，如图5所示。

图5 视轴偏角误差到FoU平面的映射

设由E，G误差造成的视轴偏角为θb，映射到O-AE平面中，方位、俯仰上的偏角分别为θv，θh。由E，G误差到θv,θh的转换关系可知，方位、俯仰视轴偏角误差仍服从高斯分布[7]，则目标出现在不确定区域联合概率密度函数

(10)

在O-AE平面，设FoU的方位、俯仰大小分别为θuv,θuh。令α=θuv/σv=θuh/σh，θv=σvv，θh=σhh，可得

(11)

当θuv=θuh=2θb=θFOU时，FoU的形状为圆或正方形；当θuv≠θuh时，FoU的形状为椭圆或长方形。图6给出了FoU视轴偏角误差标准差以及捕获概率的关系。可知，视轴偏角误差标准差越大，捕获目标的概率越高，则需要扫描捕获的FoU越大。

图6 Pu,σ和θFoU的变化趋势

2.3 FoU内捕获方案设计

目标捕获过程是在一定条件下进行，其捕获过程的5个先验条件为:1)单站车载三轴光电跟踪设备捕获目标为中轨目标；2)O-AE平面中，方位、俯仰的偏角对称分布；3)短时间扫描捕获且轨道预报数据很新；4)目标的捕获概率为98.89 %；5)设备视场半径为rfov。

由条件(1)～条件(3)可知，视轴偏角误差映射到FoU可近似为圆形区域，即θFoU=2θb，且在O-AE平面中的方位、俯仰上的联合密度函数为二维高斯分布，宜采用螺旋扫描。图7给出了捕获概率与FoU比上视轴偏角误差标准差的关系，若要满足条件4，则θFOU/2=3σb。

图7 Pu与θFoU/2σb变化趋势

视轴偏角误差的概率密度函数为

(12)

设以轨道预报值(Am,Em)为圆心，采用等线速度等距螺旋扫描如下[8]

(13)

不漏扫条件为d=rfov≥h，d为螺距，h为扫描过程视场的重叠量；成功扫描捕获目标的条件为

R=(|X(ti)-Asao(t)|2+

|Y(ti)-Esao(t)|2)1/2<|Ω|≈rfov

(14)

式中 (X(ti),Y(ti))为目标在FoU内出现的位置坐标。

等距等线速度的螺旋扫描线如图8所示，同时给出了方位轴A=(3π)/2时，E,G轴的分配情况。从图中看出，方位轴A确定时，三轴光电跟踪系统合成等距等线速度的螺旋扫描线，转动量主要是在俯仰轴上。设扫描时间间隔为Δt，则三个轴转动的角速度为

(15)

已知三个轴的转动量的情况下，改变扫描间隔时间，即可满足系统条件的前提下合成等距等线速度的螺旋扫描线。

图8 螺旋扫描线以及在三轴上的分配

在确定了FoU的特性以及三轴光电跟踪系统各轴系合成螺旋扫描的分配方式之后，根据给定的捕获概率，可计算平均捕获时间

(16)

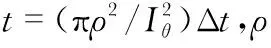
3 结束语

本文基于三轴光电跟踪系统捕获空间目标这一应用场景，建立了一种适用于现有工作模式下的三轴捕获方法。给出了FoU的形状、大小以及目标在FoU内的分布类型的具体描述。同时，在给定条件下，给出了对应的扫描捕获方法以及三轴合成螺旋扫描线在各个轴上的分配方式。在确定了FoU特性和扫描捕获方法之后，给出了评价捕获方法性能的计算公式，即平均捕获时间。为三轴光电跟踪系统捕获空间目标提供了一种参数选择方法。