基于十字及其互补形电磁微结构吸波体的传感特性*

罗 靖， 宋 健， 李敏华

(宁波大学 信息科学与技术学院，浙江 宁波 315211)

0 引 言

随着纳米技术的发展,人工电磁媒质[1～6]与包括石墨烯、光电材料、相变材料等诸多功能材料[7]相结合，实现多用途、可调控、便于集成的超器件(meta-device)[8]，为材料科学、信息科学等开辟了全新的研究空间。2008年，Landy N I等人[9]将金属谐振器和微带线置于介质板两侧，首次设计出超材料吸收器。随后双频、多频、宽频[10,11]模型陆续得以实现，极大地推进其发展。由于其强谐振，高Q值特性[12]，可应用于压力、温度、湿度、密度传感器[13]设计。Yang J J等人[14]利用负介电常数和负磁导率超介质，填充圆柱体介质波导，数值计算表明这种传感器比传统微环谐振器具备更高的灵敏度。Cong L等人[15]基于吸波腔体中电磁场局域增强效应，实现高灵敏度太赫兹(THz)传感器设计。Bakir M[16]基于开口方形谐振环加载变容二极管，通过反向偏置电压，实现频率可调传感器设计。杨杰等人[17]设计一种中心频率为9.78 GHz的超材料吸波器，通过改变待测样品相对介电常数，研究其在折射率传感方面[18]的应用。

基于人工电磁微结构的超材料吸波器，在有关待测样品介电常数敏感度研究[17,19]已有报道，有关磁导率敏感度研究很少。同时互补腔体结构模型也由于其强谐振特性得到重视[20]。本文从电场极化特性，TE/TM模斜入射角敏感特性、吸波机理，以及磁导率敏感特性四方面，仿真和实验相结合，系统比较分析十字形超材料吸波器(corss shaped matamaterial absorber,CSMA)和互补十字形超材料吸波器(complementary cross shaped metamaterial absorber,CCSMA)的特征、共同点和差异。

1 十字及其互补形微结构建模

十字形及其互补形超材料吸波器的周期单元透视图如图1(a)所示。两种吸波器均为典型的金属—介质—金属的“三明治”结构，由上下两层铜膜和中间的FR—4介质基底构成。中间介质隔离层的厚度t=1 mm，相对介电常数和损耗正切分别为4.35和0.025。顶层金属谐振结构和底层连续金属板采用导电率σ=5.8×107S/m 的铜，厚度为0.035 mm。为了便于比较，两种模型的十字和镂空十字微结构尺寸完全一致，优化后的几何尺寸如下：周期p=18.3 mm,十字/镂空十字长度l=16.08 mm，十字/镂空十字宽度w=2 mm。超材料吸波器的吸收率可由公式A(ω)=1-R(ω)-T(ω)计算。其中,R(ω)=|S11|2，T(ω)=|S21|2,A(ω),R(ω)和T(ω)分别表示吸收率，反射率和透射率。由于底板为连续铜膜，导致透射率为0，因此吸收特性仅与反射率有关。

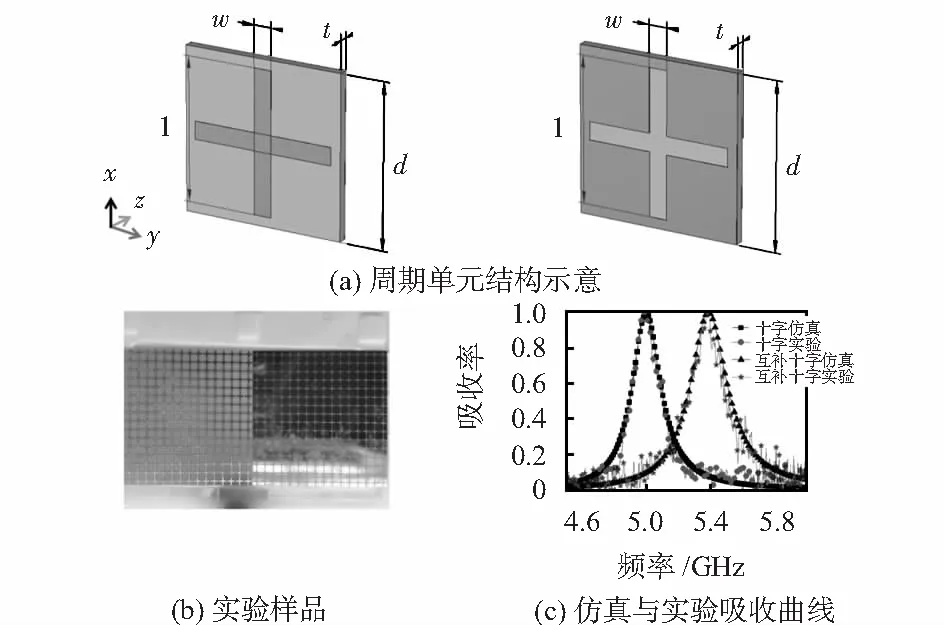
图1 CSMA和CCSMA

通过标准印刷电路板(printed circuit board,PCB)技术，周期排列16×16微结构单元，制备同样大小(292.8 mm×292.8 mm×1.07 mm)样品，如图1(b)。通过矢量网络分析仪和宽带喇叭天线，基于自由空间法，测量得到电磁波垂直入射下吸收曲线。对于CSMA，当频率为4.994 GHz时，吸收率高达99.56 %，表明该吸波器阻抗与自由空间波阻抗完美匹配。同样结构参数CCSMA，其99.79 %吸收峰出现在5.386 GHz。同时，实验数据与仿真结果一致，如图1(c)。

2 电场极化和入射角传感特性

1)在电磁波垂直入射条件下，研究CSMA和CCSMA不同电场方向对应极化角(φ) 吸收曲线变化。数值仿真及实验测量结果完全一致，如图2所示。由于两种吸波器均为四角旋转体，只需给出0°～45°数据。对不同的极化角(0°，15°，30°，45°)，CSMA和CCSMA的谐振频率没有发生偏移，实验测量吸收强度超过99.5%(图2(c)和图2(d))，证明两种结构均具备极化不敏感特性。

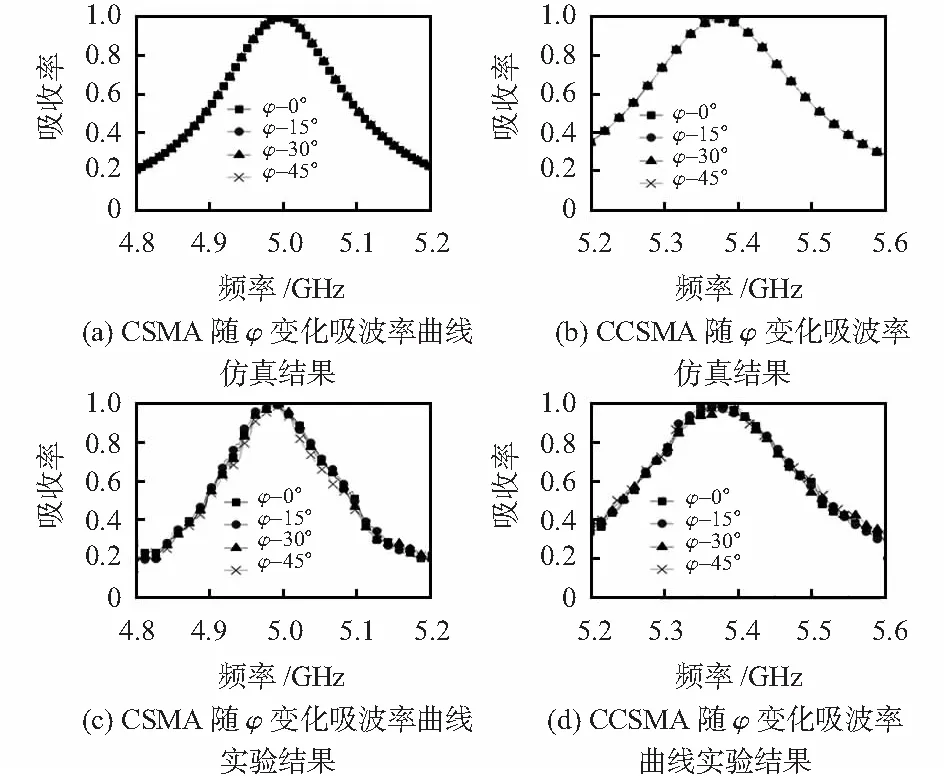
图2 电磁波垂直入射，CSMA和CCSMA不同电场方向对应φ吸收曲线

2)研究电磁波斜入射下，CSMA和CCSMA吸波器入射角传感特性。斜入射应区分TE模(电场x轴，磁场y轴，入射角围绕x轴转动)和TM模(电场y轴，磁场x轴，入射角围绕x轴转动)两种情形。首先讨论CSMA，如图3(a)和图3(c)所示，分别为TE和TM模，不同斜入射角(θ)吸收率变化曲线。对TE模，随着入射角增加，峰值吸波率逐渐减小。入射角0°～45°，吸收率仍然保持95 %以上；当θ= 60°时，吸收率下降至86.19 %。随着入射角增加(TE模)，x轴向上的电场分量没有发生改变，而y轴向上的磁场分量(x—y平面的等效投影分量)变小，不能感应足够强的表面电流，导致等效介质内部磁响应变弱(上层金属谐振单元与底层金属层的反向电流所构建的磁偶极子响应)。对TM极化波，当入射角0°～60°时，由于x—y平面的等效磁分量没有发生改变，CSMA峰值吸收率始终保持在99.7 %以上。此外，由于谐振频率主要取决于上层金属谐振单元，无论是TE还是TM模式，入射角度都没有影响表面LC振荡响应。总之，十字形超材料吸波器的谐振频率对TE/TM模均不具备入射角敏感特性，吸波强度(或反射率)可用于TE模下入射波角度传感器设计，TM模则具备宽角度入射完美吸波特性。实验结果与仿真结果基本保持一致，如图3(b)和图3(d)所示。

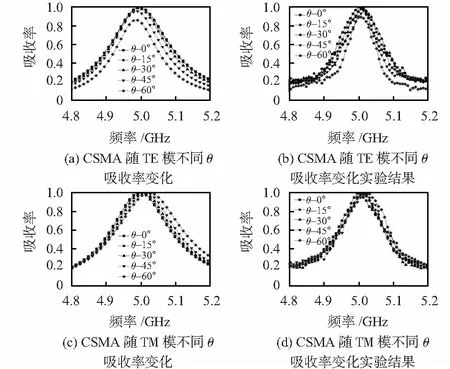
图3 电磁波斜入射下CSMA吸波器入射角传感特性

3)讨论CCSMA与斜入射角度的敏感关系，如图4所示。

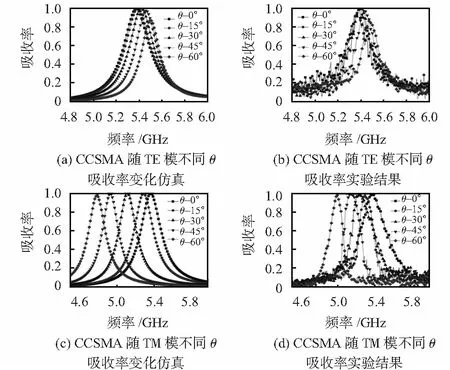
图4 电磁波斜入射下CCSMA吸波器入射角传感器特性

对于TE模极化波，与CSMA情况类似，入射磁场y轴分量随入射角增大而减小，使得CCSMA产生的磁谐振强度变弱，吸收率随之下降。同时，谐振频率略微发生蓝移，这主要来源于z轴向上的磁场分量与CCSMA上表面互补镂空结构的相互作用，所产生的额外磁响应。对于TM极化波，随着入射角的增大，吸收峰的强度基本没有发生恶化,在60°宽角度下，吸收率依旧保持在97.5 %以上。与此同时，CCSMA谐振频率向低频方向发生了显著移动，且呈现出较好的线性关系。定义频率敏感度(∂fo/∂(angle))，其中∂fo为谐振频率变化，∂(angle)为入射角度变化，TM模式下，0°～60°入射角的平均频率敏感度为9.9 MHz/(°)。由于互补结构一般具备较宽且平滑的磁谐振响应[21,22]，CCSMA谐振频率主要取决于上表面谐振器所产生的电谐振。对于互补谐振十字，其表面激励电流主要集中于短边(w参数)，而十字谐振器，长边(L参数)则承担大量电流分布(图 5、图6)。当TM模入射角增加，x—y平面磁场分量没有改变，而电场分量则逐步较少。这种不断减少的电场分量，对聚集大量电流的较短的互补结构的电谐振频率影响更大。因此，同样在TM模下，CCSMA(图4(c))对入射角的敏感性要远远强于CSMA(图3(c))。总而言之，互补十字形超材料吸波器谐振频率在TE模下具备轻微的频率偏移，其吸波强度同样可用于入射波角度传感器设计；对TM模，吸波率强度几乎没有发生恶化，但谐振峰产生明显的红移，可应用于频率传感/探测器设计。

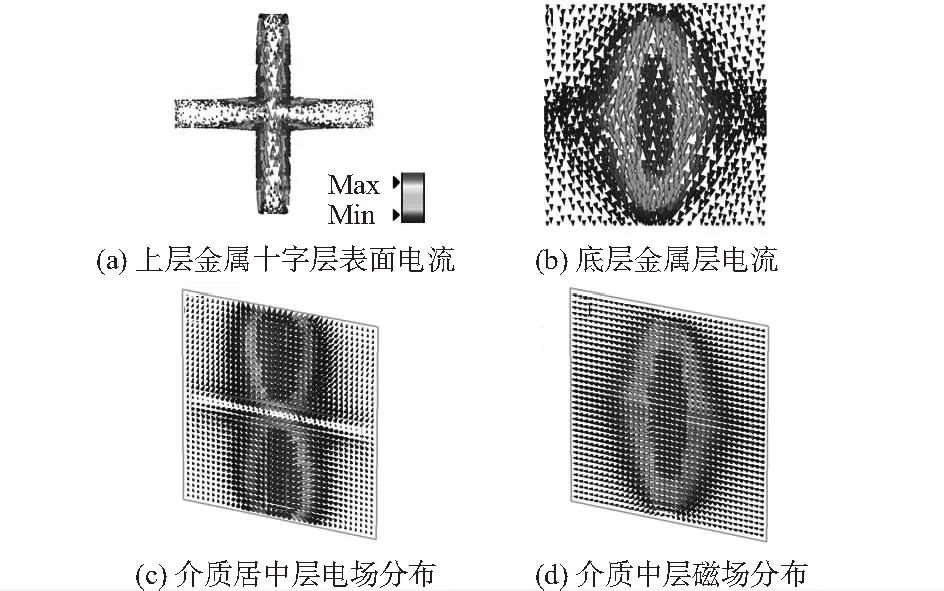
图5 CSMA表面电流分布和电磁场分布

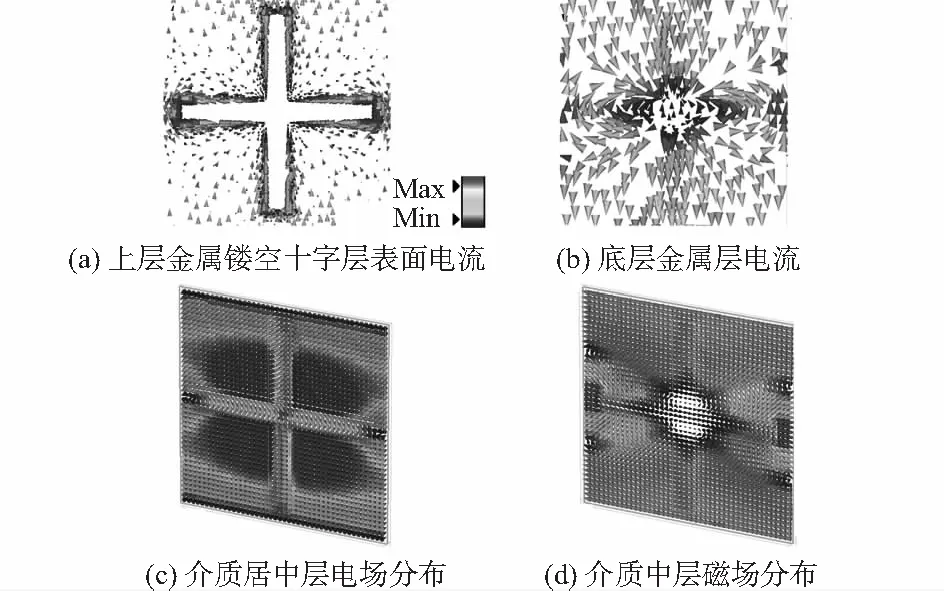
图6 CCSMA表面电流和场分布

3 物理机理分析

从表面电流分布和场的角度，分析其谐振吸波机理。对CSMA(4.994 GHz)，顶层谐振器和底层金属的表面电流分布如图5(a)、图5(b)所示。顶层感应电流主要集中在垂直金属条边缘(电场沿x轴)，电流自下而上。底层较强感应电流也刚好集中在相同位置处，由于两层金属之间电介质的填充，使得电场的相位发生改变，形成自上而下的反向电流。图5(c)为介质居中层，x—y平面的电场分布。从图中发现，在垂直金属条的上端末侧出现很强的+z轴电场分量(流入)，下端末侧出现-z轴电场分量(流出)。这种纵向的位移电流，配合顶层与底层金属(传导)电流，在x—z平面上构建近似的闭合回路，激发y轴方向的磁偶极子响应(图5(d))。其与y轴入射磁场相互耦合，从而最终产生磁谐振匹配。

图6为5.386 GHz处，CCSMA的电流和场分布图。感应电流主要集中在互补十字内框的左右边缘处，上层谐振电流方向从上至下(图6(a))，底层在对应区域，同样出现自下而上的感应电流(图5(b))。与CSMA类似，图6(c)中，大量z轴方向电场集中于互补十字的四个内直角区域处，其与上下层金属层电流配合，形成两个等效的磁偶极子响应，如图6(d)所示的磁场分量。值得注意的是，无论CSMA还是CCSMA，z轴向上的电场分量都起着至关重要的作用。一方面其与上下层金属谐振电流相配合，构建与入射磁场方向一致(水平方向)的磁偶极子响应，从而实现磁匹配；另一方面，由于有耗介质的存在，z轴方向的位移电流会最终以热能形式耗散在介质层中，因此与传统欧姆损耗不同，超材料吸波机理往往来源于介质损耗。

4 基于CSMA和CCSMA磁传感特性研究

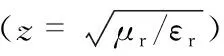
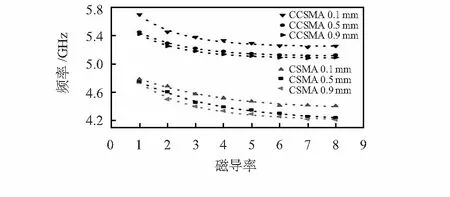
图7 待测样品层厚度为0.1，0.5，0.9 mm下，CSMA和CCSMA谐振频率随磁导率变化移动及其拟合曲线

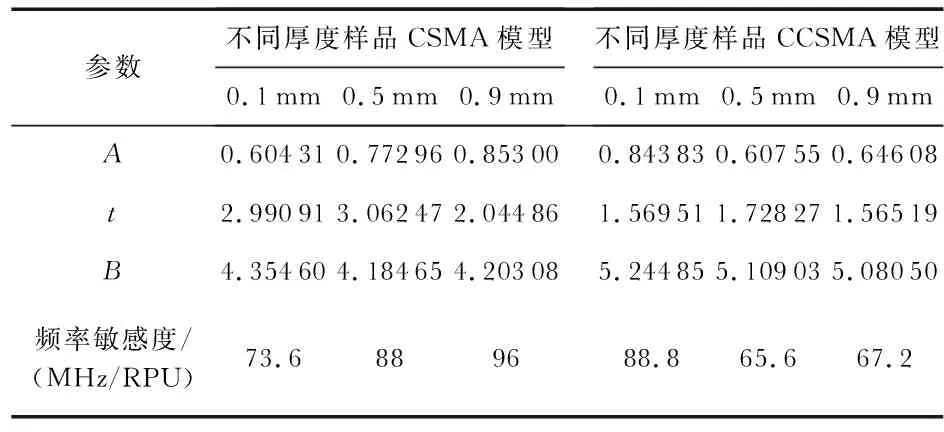
表1 图7对应的拟合曲线函数取值及平均频率敏感度(磁导率取值1～6)

图8为吸波率与磁导率敏感程度曲线。对于CCSMA，其吸波率并没有随着待测样品磁导率的变化而发生改变。所选取的3种不同样品厚度，对其吸波率也没有明显的影响关系，这种关系与图4所讨论的TM模下宽角入射情况类似。对互补结构，由于其具备相对较宽且平滑的磁响应谐振，表面样品磁导率变化对吸波率强度影响可以忽略。吸波率(相对磁导率)敏感度可定义为∂(Abs)/∂μ，∂(Abs)为吸波率的变化(百分比表示)，∂μ为磁导率变化。对于CSMA，随着样品厚度增加，其吸波率随着磁导率增加明显减小，且呈现良好的线性关系，因此可以通过直线拟合：Abs=A+Bμ。对应不同情况系数取值如表2所示。随着厚度增加，吸波率敏感度从0.21 %/RPU(relative permeability unit)增加至1.96 %/RPU。总而言之，CSMA吸波强度随待测样品磁导率增加而呈线性递减，且厚度越大，敏感度越高；CCSMA与样品磁导率没有依赖关系，仍旧保持完美吸收。

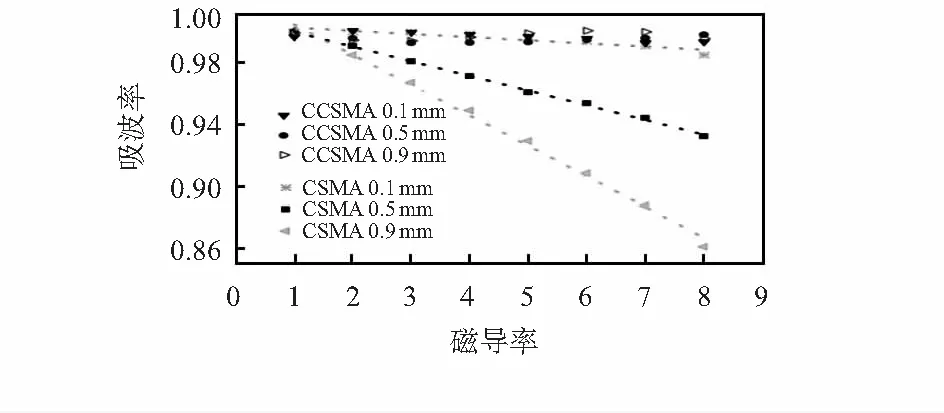
图8 待测样品层厚度为0.1，0.5,0.9 mm下，CSMA和CCSMA吸波率随磁导率变化及其拟合直线(仅针对CSMA)

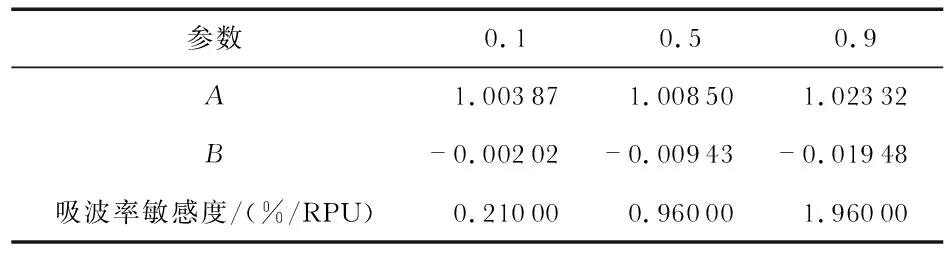
表2 图8对应的CSMA拟合直线函数取值及吸波率敏感度

5 结 论

基于CSMA和CCSMA微结构，构建超材料吸波器模型。经分析，两种模型吸波强度(或反射率)均可用于TE模下入射波角度传感器设计，CSMA谐振频率对TE和TM模不具备入射角敏感特性，而CCSMA对TM模则具备宽角度入射完美吸波特性，其谐振峰发生明显红移，0°～60°入射角的平均频率敏感度为9.9 MHz/(°)，可应用于频率传感/探测器设计。将吸波体表面覆盖不同厚度的待测样品，研究相对磁导率对谐振频率和吸波强度的影响。两种模型谐振频率均随着磁导率增加而红移，CSMA吸波强度呈线性递减，且随样品厚度增加，吸波率敏感度从0.21 %/RPU增加至1.96 %/RPU。厚度越大，敏感度越高；CCSMA与磁导率没有依赖关系，仍旧保持完美吸收。