静电微驱动器的高阶自激振动与数值仿真
陈筠菲, 漆明净
(1.北京航空航天大学 能源与动力工程学院,北京 100191;2.加州大学伯克利分校 机械工程系,美国 加州 伯克利 94721740)
0 引 言
微驱动器是微机电系统(micro-electro-mechanical system,MEMS)中的执行机构,主要作用是输出力、力矩、位移等物理量[1,2]。传统的微型静电驱动器在交流电压的驱动下进行受迫振动,由于“吸合效应”使输出位移难以进一步增加。文献[3]提出一种新型基于自激振动的微型静电驱动器,相较于传统静电驱动器在输出位移上有了很大提升。
目前,国内外关于高阶自激振动的研究集中于桥梁拉紧索在风雨的激励下进行的振动和航空发动机叶片颤振[4]等方面,但在微观层面,高阶自激振动很少被观察到,对这一现象的研究很少。
在非线性振动系统中经常出现跳跃现象,其中微小的参数变化可能导致输出的显著变化。跳跃现象有两种类型:振幅跳跃和频率跳跃。振幅跳跃现象在MEMS驱动器中十分常见,频率跳跃相对来说则极为罕见[5]。原因是目前大多数MEMS驱动器都是基于强迫振动的原理,其输出频率或者是恒定的,或者是基于输入频率连续变化的。频率跳跃在MEMS器件,如高灵敏度传感器和多模式致动器等的应用中具有巨大的潜力。
本文描述了新型静电驱动器中出现的高阶自激振动现象和频率跳跃现象,并对其进行了数值仿真,获得试验条件与振型之间的内在联系,以指导后续试验。
1 高阶自激振动现象
驱动器示意图如图 1所示。驱动器由悬臂梁、基座和一对电极组成。悬臂梁由长40 mm,直径50 μm的键合铝丝制成。由聚氯乙烯(poly-vinyl-chloride,PVC)板制成的基座与电路绝缘。电极是分别连接到直流电源正极和负极的两个金属针,两电极之间的间距为5 mm。悬臂梁一端固支于基座上,静止时位于正负电极连线的中垂线上,悬臂梁根部和电极之间的距离记为d。悬臂梁的振动情况由高速相机捕捉。

图1 驱动器示意
当没有输入电压(VDC)时悬臂梁保持直线。随着VDC的增加,一旦VDC超过吸附电压VP,悬臂梁将首先弯向正极,并与正极接触。在与正极接触之后,悬臂梁将被充正电,并在静电排斥力及其弹性恢复力的共同作用下向负极运动,与负极接触。类似地,悬臂梁与负极接触后将向正极方向运动。因此,在运动引起的静电力及弹性恢复力的共同作用下,悬臂梁可以维持稳定的振动。由于驱动器中悬臂梁的振动是由一个恒定的直流电压驱动的,因此悬臂梁所进行的是自激振动。
当改变输入电压VDC或悬臂梁根部与电极之间的距离d时,可以观察到悬臂梁的振动由一阶振动变为存在一个稳定节点的二阶振动,同时振动频率急剧增加,出现频率跳跃现象。
距离d保持不变时,通过改变输入电压VDC可以实现振型转换和频率跳跃。图2(a)与图2(b)相比,距离d保持不变,输入电压VDC由4 kV增加到5 kV,振型由一阶变为二阶,振动频率由27.03 Hz跃变到108.48 Hz。振型转换和频率跳跃也可以通过保持输入电压VDC不变,改变距离d来实现。图2(a)与图2(c)相比,输入电压VDC保持不变,距离d由2 cm增加到3 cm,振型由一阶变为二阶,振动频率由27.03 Hz跃变到69.12 Hz。
在试验中观察到了两种不同的二阶振型:振动节点位于电极外侧的二阶振型(如图2(b))和振动节点位于电极和基座之间的二阶振型(如图2(c))。

图2 二阶自激振动示意图与高速相机图
2 数值仿真模型建立
本文采用梁模型为欧拉—伯努利梁。在一个周期内,根据是否与电极接触,悬臂梁的振动可以划分为非碰撞阶段和碰撞阶段。在非碰撞阶段(图3),作用在悬臂梁上的力主要有静电力FE和空气阻力FD,FE和FD作用在梁的每个无穷小微段上。在碰撞阶段,作用在悬臂梁上的力主要有FE,FD和碰撞力FC,FC为作用在x=d处的集中力。

图3 悬臂梁在非碰撞阶段的受力情况
针对非碰撞阶段,根据欧拉—伯努利梁的横向振动微分方程,梁上无穷小微段的运动方程为
(1)
式中t为时间,x为微段在悬臂梁中的位置,y为其挠度,c为空气的粘滞系数。
针对碰撞阶段利用动量平衡法[7,8],假设碰撞在瞬间完成,通过恢复系数描述碰撞前后碰撞体的速度变化而不考虑撞击过程的细节,求解得到碰撞后柔性连续体上各点的速度。由于碰撞发生时,碰撞点受到很大的冲力,静电力和空气阻力等大小有限的力可以忽略不计。
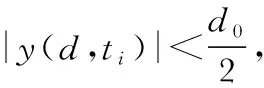





3 数值仿真结果
为了模拟输入电压VDC和距离d对振动形式和振动频率的影响,依旧选取VDC=4.0 kV,d=20 mm,VDC=5.0 kV,d=20 mm 以及VDC=4.0 kV,d=30 mm进行数值仿真。通过MATLAB的数值方法求解控制方程,图4~图6给出了不同VDC和d下梁上各点挠度随时间的变化情况和1/2周期内的挠度—位置曲线。据图可知,数值仿真的结果均与试验中观察到的振动形式相符。
当VDC=4 kV,d=20 mm时(图4),悬臂梁在振动过程中保持一阶振动模式。

图4 VDC=4 kV,d=20 mm时数值仿真结果
当VDC=5 kV,d=20 mm时(图5),在振动开始后,悬臂梁的振型迅速由一阶变为二阶。根据图5(b)可知,与试验中观察到的现象类似,节点的位置相对稳定并且处于电极外侧。

图5 VDC=5 kV,d=20 mm时数值仿真结果
当VDC=4 kV,d=30 mm时(图6),振型在振动开始后约9 ms由一阶转化为二阶。根据图6(b)可知,振动节点的位置相对稳定并且处于悬臂梁根部与电极之间,与试验中观察到的现象相符。

图6 VDC=4 kV,d=30 mm时数值仿真结果
将试验测得的振动频率与数值仿真结果进行对比,VDC=4 kV,d=20 mm时,试验结果为27.03 Hz,数值结果为74.56 Hz;VDC=5 kV,d=20 mm时,试验结果为108.48 Hz,数值结果为235.46 Hz;VDC=4 kV,d=30 mm时,试验结果为69.12 Hz数值结果为256.15 Hz。3种情况下数值仿真频率都高于其相应的试验频率,并且出现频率跳跃现象。
4 结 论
建立了一个静电微驱动器的自激振动模型,研究输入电压VDC和悬臂梁根部与电极之间的距离d对振型和振动频率的影响,利用MATLAB对其进行数值仿真。与试验结果对比可知,数值仿真所得的振型与相应试验结果一致,计算所得的频率高于相应试验振动频率,数值仿真结果中也出现频率跳跃现象。该数值模型可以为选择试件材料和试验条件提供参考和借鉴,指导后续驱动器设计。

