习题设计渐臻数学猜想能力培养
周伟杰
摘要:猜想—验证—应用是当前小学数学课堂教学的主流模式,可这种随处可见的“猜想课堂”因为依托基础薄弱、数理逻辑违和、视域局限狭窄、表达方式单一等问题,影响了学生猜想能力培养的正面展开。本文以翔实的习题课例研究为载体,围绕数学猜想内容的设计、数学猜想时机的选择、数学猜想方法地展开这三个方面展开论述,进一步阐明了数学猜想能力培养的重要性。
关键词:习题设计 数学猜想能力 培养
猜想,是一种不确定的预见,更是一种想象。数学猜想则是数学思维不断发展的媒介,是学生数学学习的基本能力之一。在当前的数学课堂教学中,因为存在猜想依托基础薄弱、数理逻辑违和、视域局限狭窄、表达方式单一等诸多问题,影响了学生数学猜想能力培养的正面展开。因此,要想实现“猜想课堂”,教师必须以学生的思维操作为基础,以实际应用的分析与验证尝试为动力,以“猜想—验证—应用”的科学认知定位为目标,从多层面、多角度激发学生的创新能力和探究潜能。
一、基点:数学猜想内容的设计
教会学生猜想的第一步是设计数学猜想的内容,因为一个优质猜想内容的设计,能让学生在动态联系的过程中,有意识地对知识的真伪先判断再选择、先猜想再验证,通过多种感官的参与,获得自身需求的最大化。在课堂教学中,教师应合理选择和运用相关的教学素材,通过多种教学方法,设计新颖、实效的猜想内容,这也是丰盈“猜想课堂”的重要方式之一。
1.因“境”而生的数学猜想
在设计猜想内容时,教师必须兼顾数学教学资源的科学性,通过多种情境创设的载体作用,为猜想氛围提供充足的时间和空间,促进学生预见性思考的形成。
案例一:植树问题
片段呈現:
教师说:“植树节到了,希望小学给五(2)班布置了绿化植树的任务,校门口到食堂的路程长30米,要求五(2)班的学生在路的左侧每隔6米植一棵树,猜一猜,他们班一共植了几棵树?
学生1说:“5棵。”
学生2说:“我觉得是6棵。”
教师问:“还有其他不同的想法吗?”
学生3说:“我觉得可能是4棵。”
教师问:“这么多的猜测到底谁的想法是正确的呢?大家能用自己喜欢的方法证明一下吗?”
本课教学旨在通过猜测、验证(操作),让学生理解植树问题的三种关系,并运用这种关系模型解决日常生活中的其他问题。因此,在本课教学中,教师融入了新颖的生活情境,为学生提供了猜想的平台,让学生在相互争论中认识到数学验证的必要性,提高了学生的自主参与度,并感受了数学问题隐藏的趣味性。
2.因“疑”而生的数学猜想
问题是数学学习的起因,是知识获取的经过,更是知识运用的最终结果。教师利用问题引起学生猜测的本能,不仅能引导学生快速、准确地接受知识,还能在解决问题的过程中,促使学生形成猜想意识,提高学生积极思考问题的能力。
案例二:三角形的分类练习
教师出示课件,如图1所示:
图1
教师问:“有3个三角形被纸遮住了一部分,你能快速判断出那是什么三角形吗?”
学生1说:“A是钝角三角形,B是钝角三角形,C是直角三角形。”
教师问:“你们都是这样想的吗?”
学生2说:“我觉得B也可能是直角三角形。”
教师问:“哦,说说你的想法?”
学生2说:“因为有一个角是直角的三角形是直角三角形,如果我们看到的这个角刚好是直角三角形中两个锐角中的一个,那它不就是直角三角形吗?”
教师问 :“其他同学有什么想说的吗?”
学生3说:“我赞同他的想法。这个可能是存在的,而且我想补充,这个三角形也可能是钝角三角形。”
教师问:“通过这个的练习,你们有什么话想说?”
学生1说:“只看到一个锐角,并不一定是锐角三角形。”
学生2说:“判断一个三角形的类型最好要确定两个角。”
小学生的思维活动是独特又具有个性化的,经常会有许多奇思妙想,但有时他们的猜想往往缺乏理论依据,这就需要教师随时调整问题,引导学生根据提供的练习素材,通过想象和对比,运用一些数学解题方法,对新情况、新问题做出具有一定方向的、有理有据的猜想。本案例教学旨在通过三角形分类的练习,进一步理解各种三角形的特征,培养学生的逻辑推理能力。在本教学案例中,教师利用三个被遮住一部分的三角形让学生进行辨析。为了让学生学会全面地思考问题,教师通过“你们对他的想法有什么想说的”这一问题,将学生的猜想引到合理的方向,规避学生不切实际的猜想,达成练习的最终目标。
二、焦点:数学猜想时机的选择
数学学习最初级的思维过程是指学生能最简单地分析、推理、探究一些数学表象,然后捕捉新知识的生长点,这样的能力可以广义地称之为猜想。猜想不是一种臆想,它除了以一定素材为载体,还需要以时机上的合理安排为依托,通过追溯学生猜想背后的想法,探究活动开展的立体面。
1.因操作萌发的数学猜想
天性好玩的小学生和抽象的数学学习之间存在很大的差异性,为了减少这样的差异性,在数学练习过程中,教师应给学生提供大量实践操作的机会,有目的、有组织地让学生观察和操作,检验猜测的科学性。这样一来,不仅可以满足学生的好奇心,还可以引导学生在观察操作中进行合理猜想。
案例三:长方形和正方形的认识
片段呈现:
教师问:“同学们,你们猜一猜长方形的四条边之间有什么关系?”
学生1说:“上下两条边长一些,左右两条边短一些。”
学生2说:“上下两条边一样长,左右两条边一样长。”
教师说:“我们来验证一下这些猜想正确吗?你们有什么好方法能证明吗?请小组之间交流一下,选择最恰当的方法来验证自己的猜想。”
学生3说:“我们组的结论是四条边两两相等。我们选择了用直尺测量,结果发现两条长边是10厘米,是相等的。两条短边是7厘米,也是相等的。”
学生4说:“我们想到折一折的方法,把长方形上下对折,结果发现上下两条边完全重合,说明上下两条边一样长。接着,又左右对折,发现也是重合的,证明两条短边一样长。”
教师说:“通过量一量、折一折,我们验证了长方形的对边相等。看来猜测固然重要,但验证也很重要。”
科学研究证明,教师应允许学生借用自己的经验基础进行大胆的假说创造。在数学课堂教学中,教师必须深入思考如何开发学生的猜想能力。在本教学案例中,学生在教师的引导下进行了多种合理猜想,接着以小组合作交流的方式进行了实践活动(操作验证),通过尺子量、图形对折的方法,让每个学生都调动多种感官参与学习活动。在整个探究过程中,学生不仅享受了学习的快乐,还探究了新知。
2.因联想激发的数学猜想
猜想是一种创造新思维,每个人都有猜想的潜力,为了充分发挥学生的潜在能力,教师必须培养学生从数学角度观察和思考遇到的问题,并运用所学知识解释数量关系与空间形式的能力。因此,教师要采取多种教学方法激活学生学习的内驱力,挖掘学生的潜能,以相应的习题为载体,不断强化学生的思维习惯,促使学生迸发出创新的火花。
案例四:四边形的分类综合练习
片段呈现:
教师问:“信封里是一个四边形,猜一猜可能是什么形状?(露出一个锐角)”
教师问:“你能猜出它是哪种四边形吗?会是长方形和正方形吗?为什么?(露出一个直角)”
教师问:“它会是什么形状呢?可能是平行四边形吗?如果露出的这个角是钝角呢?”
教师问:“我们继续猜,我这里的一个平面图形可以剪成高相等的一个直角三角形和一个直角梯形,你们猜一猜,这个平面图形原来是什么形状?”
在本教学案例中,教师以“猜图形”的游戏情境作为习题呈现的载体,通过层层递进的问题情境进行串联,让学生自觉联系原有的知识储备,合理猜测不同四边形的特征。学生在加深理解四边形知识的同时,也掌握了利用“迁移”的方法、“迁移”的思考方式来解决问题。
三、落点:数学猜想方法的展开
在数学教学中,教师反对将简单、有限的知识聚合视为学生学习的终极目标,而是提倡通过渐进式的处理方式,培养学生的猜想能力,教会学生正确的猜想方法,并结合数学习题让学生从多角度汲取知识,发展数学思维,同时运用学到的知识解决实际问题。
1.因练习衍生的数学猜想
少铺垫,少过程,是当前教材呈现出的软肋之处,这会让学生觉得数学知识如嚼“顽石”,难以理解。因此,教师要从练习课的题源入手,进行二度开发,降低学生的学习难度,并借助新旧知识间的矛盾冲突,形成多次铺垫,创设“丰厚”的内隐,让学生在此基础上学会正确的猜想。
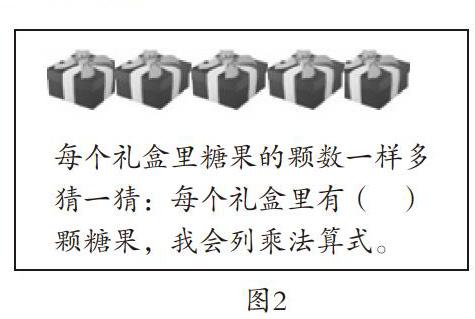
图2
笔者设计了一道练习题,如图2所示,以5个装有糖果的礼盒为学习的媒介,教师借用建构主义的教学观分层展开,设计了框架式的题组,猜一猜每个礼盒里有多少颗糖果,以帮助学生正确地展开猜想。
在第一层练习时,教师先让学生无序地猜测每个盒子中糖果的颗数,并试着让学生列出相应的乘法算式。在广泛获取信息的基础上,学生通过讨论、归纳发现了规律:虽然猜的颗数不一样,但都有5个几,就可以用乘法算式5×()来表示。紧接着,教师确定每盒的颗数是7,如果有9盒、20盒、100盒……n盒,进而引导学生试着列出相应的乘法算式。在比较、归结中,学生会發现虽然盒数都不一样,都是表示有几个7,就可以写成7×()。这样一来,既拓宽了学生思维活动的空间,又沟通了相同加数与相同加数的个数知识间的联系,将无形的数学思想方法以问题解决的方式加以巩固,引领学生进行深刻地反思与提炼,感悟数学思想方法的价值性。
2.因总结拓延的数学猜想
数学思想方法是对数学知识的本质认识,虽隐于知识之中,却无时无刻不主导着学生知识的形成与发展。可是,无形的数学思想方法最容易被教师忽视、隐藏,久而久之,就影响了学生知识的全面获得。因此,在平常的数学教学中,教师要将猜想不断延伸,深层次地挖掘教学素材背后的隐性思想方法,引领学生进行深刻的反思与提炼,感悟猜想方法的价值。如在教授新内容后,教师可以让学生猜一猜以后可能学习什么内容,也可以猜想今天学习的内容有什么作用。这样一来,不仅能激发学生对后面知识的学习兴趣,还能让学生的数学知识更具系统性和完整性。
教学过程是一个不断变化的过程,正是因为有这样或那样的不确定,才使得知识获得的过程更具生动性。猜想是数学思维和数学活动的重要方法,为了最大限度地发挥猜想的价值,教师要从实际出发,把控和创造各种猜想因素和时机,灵活运用科学的教学方法,引导学生进行合理有效的猜想,并在完整验证的过程中,实现认知水平的提升和思维的飞跃。
参考文献:
[1]樊继学.借助数学猜想提升思维水平[J].广西教育,2015,(45).
[2]潘龙汛.让数学课堂在猜想中出彩[J].数学大世界(上旬),2016,(12).
[3]黄哲.提升素养,智创绚丽多“猜”的数学舞台[J].小学教学参考,2014,(24).
[4]赵希韶.激发、提高、巩固,阶段式提升学生的猜想能力[J].小学教学参考,2017,(2).
(作者单位:浙江省天台县坦头镇中心小学)

