2019年高考数学全国Ⅰ卷理科与课程标准一致性分析

康雯　唐剑岚　周宇剑

摘 要：采用韦伯一致性分析法来衡量2019年高考数学（理科）全国Ⅰ卷与课程标准的一致性。发现2019年高考数学（理科）全国Ⅰ卷与课程标准在知识种类、知识深度和知识分布平衡度方面有较好的一致性，但在知识广度方面还有所欠缺。建议：命题者提升试题考查的广度，优化综合新题型;备考者则要注重函数、几何与代数两个主题的学习，重视问题解决能力的培养，注重核心素养的综合提升。

关键词：高考数学;数学全国卷;课程标准;一致性;韦伯一致性

一、 问题提出

2019年高考数学成为热议话题，理科全国Ⅰ卷更是被考生吐槽为“换了个碗”。2019年为高考综合改革过渡年，数学全国Ⅰ卷（理科）难度如何？与2017年版的普通高中数学课程标准（以下简称课程标准）的一致性程度如何？为衡量该卷与课程标准的一致性，本文采用韦伯一致性分析方法进行研究。

二、 研究工具

韦伯一致性分析方法由美国学者诺曼·韦伯（Norman L·Webb）提出并发展，在进行一致性分析时，把课程标准的内容目标进行分级，从而构成“金字塔”式的体系，韦伯一致性分析分别从“知识种类”“知识深度”“知识广度”和“知识分布平衡度”四个维度衡量学业评价与课程标准的一致性。

三、 数据统计与分析

（一） 知识种类一致性分析

知识种类一致性主要分析试卷所考查的内容与课程标准中规定的内容是否一致。根据韦伯一致性分析法，必须至少有六次命中某主题的内容才能认定试卷与课程标准在某主题一致性比较好，低于六次则认为试卷与课程标准在某领域知识种类方面的一致性较差。

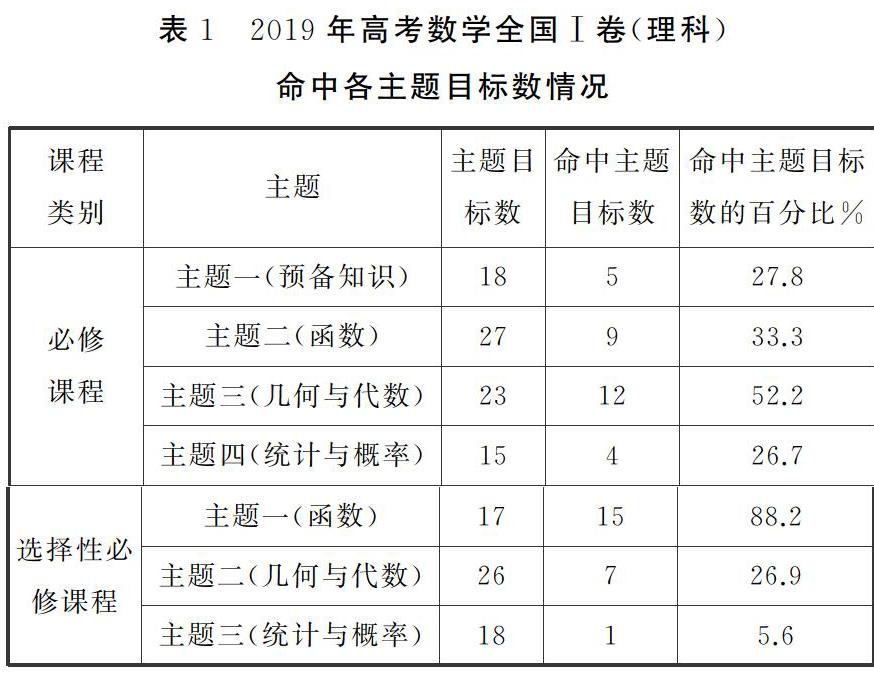
统计2019年高考数学全国Ⅰ卷（理科）考查到的各主题的目标数据如下表1：

由表1可知，除必修模块主题一、主题四和选择性必修模块主题三外，其余四个主题均与课程标准在知识种类上有较好的一致性。其中选择性必修模块主题一和必修模块主题三被击中的次数分别高达15和12次。

（二） 知识广度一致性分析

知识广度的一致性是分析高考试题实际考查的知识范围与课程标准中要求学生掌握的知识范围是否一致。试卷命中的目标数目大于某主题具体目标的50%就认为试卷的广度与课程标准某主题较一致。

统计2019年高考数学全国Ⅰ卷（理科）的相关数据，计算各主题中试题命中的目标数与总目标数的百分比见上表1，从上表1可得，必修模块的主题三和选择性必修模块的主题一命中主题目标数的百分比超过50%，在知识广度方面与课程标准有较好的一致性。总体看，2019年高考数学全国Ⅰ卷（理科）与课程标准的一致性较差。

（三） 知识深度一致性分析

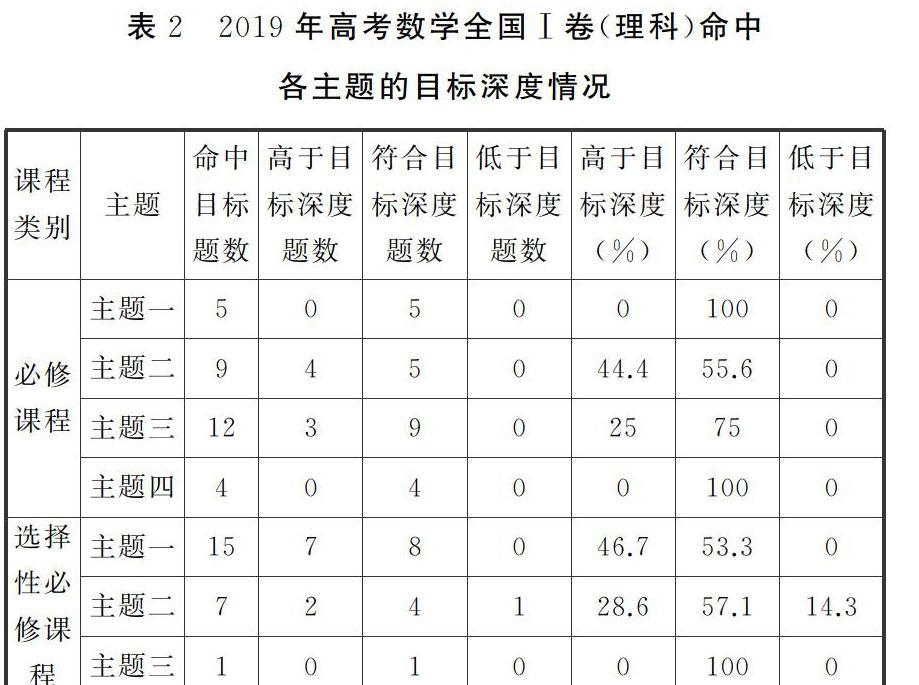
知识深度一致性是指试卷所考查内容的深度水平与课程标准中对知识内容深度的规定是否一致。知识深度一致性的判断标准是：试卷对某主题至少有50%命中课程标准对某主题所要求的符合目标深度的认知水平。课程标准将知识点分为了解、理解、掌握三个层次。借助教育部考试中心发布的2019年理科数学试题参考答案，以及相关教辅机构对高考试题所考查知识点的分析，分析试题所考查的知识点，得出试题所考查知识点的水平。据此将2019年数学全国Ⅰ卷（理科）所考查知识点的层次水平与《课程标准》中的具体目标所属层次水平进行比较，统计相关数据得到下表2：

由表2可知，2019年高考数学全国Ⅰ卷（理科）与课程标准在知识深度方面有较好的一致性。其中，必修模块的主题一、主题四、选择性必修模块的主题三在知识深度方面与课程标准的一致性程度为100%，与课程标准所要求掌握的水平吻合度较高。必修模块的主题二和选择性必修模块的主题一分别有44.4%、46.7%的考查目标高于课程标准要求水平，可见高考对函数要求较高。

（四） 知识分布平衡一致性分析

知识分布平衡一致性是考查高考卷重视某一目标的程度。根据韦伯一致性分析，知识分布平衡程度只用来考虑那些至少被命中过一次的目标。主要用知识分布平衡指数来衡量知识分布平衡程度，其计算公式为：

平衡性指数=1-1O-IKH2

其中，O=被命中的某内容标准所包括的目标总数，IK=命中单元内容题目数，H=命中具体目标总数。一般认为，平衡指数在0.6-0.7之间认为知识分布的平衡程度勉强达标，高于0.7则认为试题的分布平衡程度比较好，低于0.6则认为知识的分布平衡程度比较差。

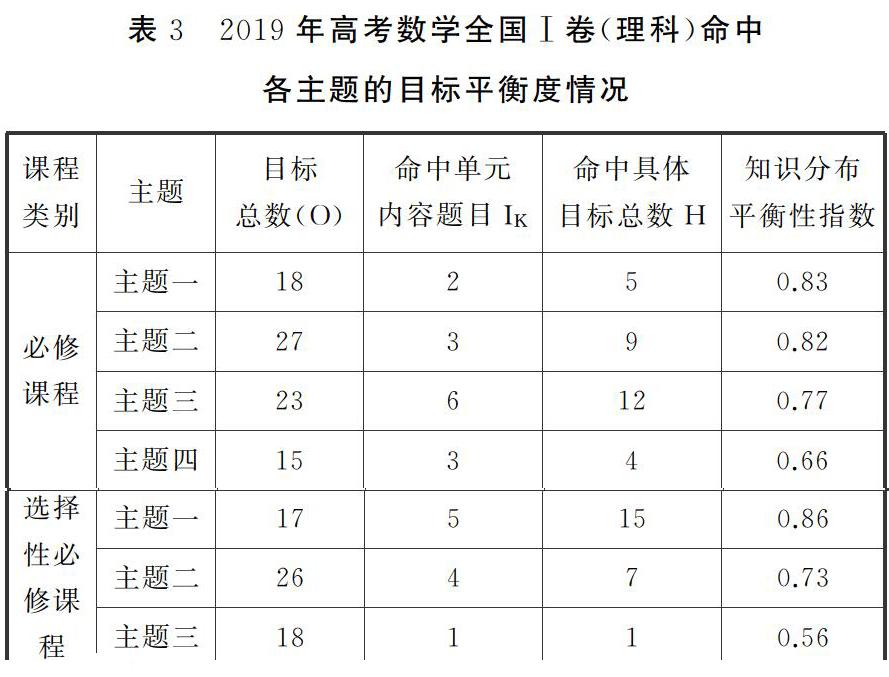
統计相关数据，计算各主题的知识平衡性指数得到下表3：

据上表3可知，选择性必修模块的主题三在知识分布平衡度方面与课程标准的一致性稍差。总体看，2019年高考数学全国Ⅰ卷（理科）与课程标准在知识分布平衡度方面有较好的一致性。

四、 建议

（一） 复习备考建议

1. 综合掌握所学知识，会灵活运用。特别是函数，不仅要掌握函数的相关性质，对函数的图象、单调性、周期性等都应有清晰的了解，要重视数形结合，把函数与其图象密切联系起来。

2. 必修课程主题二（函数）、选择性必修课程主题一（函数）和主题二（几何与代数）考查的内容深度相对较高，题量也偏多，在学习和复习的过程中宜适当多分配时间。

3. 重视问题解决能力的培养。近些年来，课程改革一直在强调核心素养的培养，数学建模、问题解决能力的培养应该被重视。

（二） 命题建议

1. 重视试题所考查目标的广度。2019年高考数学全国Ⅰ卷（理科）有五个主题（共七个主题）的目标与课程标准在知识广度上一致性较差。出现对重要定理进行了多次考查的情况，有些题目所考查的知识点比较少，综合性相对较弱。因此，需要在知识广度考查上下功夫。

2. 优化考查学生核心素养的题型。试卷考查了学生分析问题、解决问题的能力，但在发现问题和提出问题部分仍有欠缺，有挖掘的空间。（通讯作者：周宇剑）

参考文献：

[1]诺曼·韦伯，张强雨译.判断评价与课程标准一致性的若干问题[J].比较教育研究，2011（12）：83-89.

[2]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.

作者简介：

康雯，湖南省永州市，湖南科技学院;广西壮族自治区桂林市，广西师范大学;

唐剑岚，广西壮族自治区桂林市，广西师范大学;

周宇剑，湖南省永州市，湖南科技学院。