计算Drazin逆的一个方法∗

阿布都卡的·吾甫

(新疆大学数学与系统科学学院，新疆 乌鲁木齐 830046)

0 前言

关于Drazin 逆有相似于Jacobson 引理的结果,即1−ab Drazin 可逆当且仅当1−ba Drazin 可逆.在文献中此结果的证明非常简单: 设1−ab Drazin 可逆,则存在c ∈R 和自然数k 使得

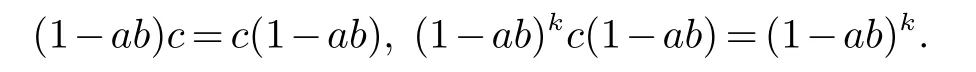
这时通过直接计算我们有

即1+bca 是1−ba 的Drazin 逆（见[1]）.现在我们要讨论1+bca 是如何被想出来的？有没有一种用等式

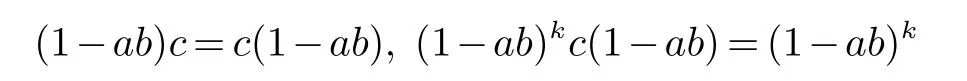
来算出1+bca 的方法？

在本文，当Drazin 指数等于2 时，我们通过Gröbner-Shirshov 基方法给出用等式

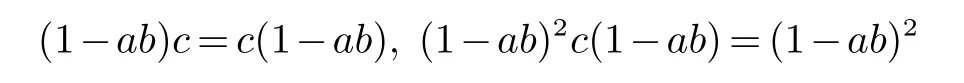
来算出1+bca 的方法（见[1]）.

1 代数的Gröbner-Shirshov基

代数的Gröbner-Shirshov 基理论的基本概念和结果见文献[5].

设X 是一个非空集合，其元素我们称字母，X∗是由X 中的元素生成词构成的自由幺半群，其中单位元是空词1.设K 是一个域，我们用K X 表示由X 生成的自由结合K−代数,那么X∗是K X 的一组K−线性基.对任意词w ∈X∗,我们用|w| 表示其长度，也就是w 所包含的字母个数.为了确定任意非零多项式f ∈K X 的首项，我们在集合X 上选取一个良序<，此序在幺半群X∗上诱导出一个序，我们仍用<来表示此序.如果序<与幺半群X∗的乘法运算相容，即对任意u,v,w ∈X∗，有u 如下:

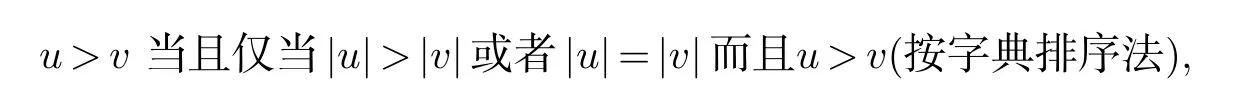
则此序是单项式序,记为deg-lex 序.本文我们用此序.如果首项的系数是1，则多项式f 称为首一多项式.

设< 是X∗上的单项式序，对于任意两个首一多项式f 和g，我们定义他们的合成如下：

(1)若存在w ∈X∗,使得其中a,b ∈X∗,且那么称(f,g)w=fb−ag 为f 和g 相对于w的相交合成.

我们把相交合成和包含合成统称为合成.

设S ⊆K X 是由一些首一多项式组成的非空集合.对任意f,g ∈K X，如果(f,g)w= αiaisibi,其中αi∈K,ai,bi∈X∗,si∈S 且那么称(f,g)w对模S 平凡,并记

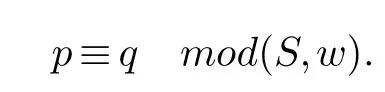
设< 是X∗上的一个单项式序，S ⊆K X 是首一多项式的非空集合，Id(S) 是代数K X 的由S 生成的双边理想.如果集合S 上所有多项式的合成都是对模S 平凡,那么我们称S 是理想Id(S) 在代数K X 中的一个Gröbner-Shirshov 基.因此一个元素a ∈Id(S) 当且仅当a ≡0 mod(S.w).

下述引理是Gröbner-Shirshov 基理论中的核心结果.

引理1(钻石合成引理) 设S ⊆K X 是首一多项式的一个非空集合，< 是X∗上的一个单项式序.下面三个命题等价：

(1) S 是一个Gröbner Shirshov 基.

(2) 若0 =f ∈Id(S),则存在s ∈S 和a,b ∈X∗,使得

2 计算Drazin逆

设R 是有单位元的环,且a,b ∈R.我们假设存在c ∈R 使得

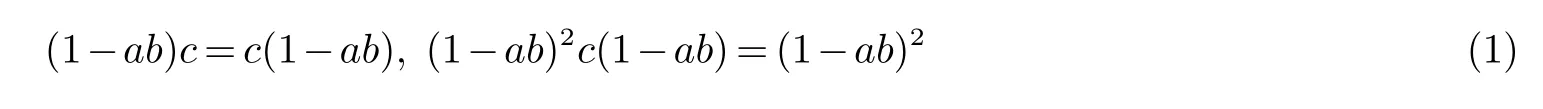
即1−ab 具有以Drazin 指数为2 的Drazin 逆c.下面我们计算1−ba 的以Drazin 指数为2 的Drazin 逆.

设A 是由a,b,c 生成的，并且满足关系(1) 的Z−代数.我们要在A 中找一个元素x 使得

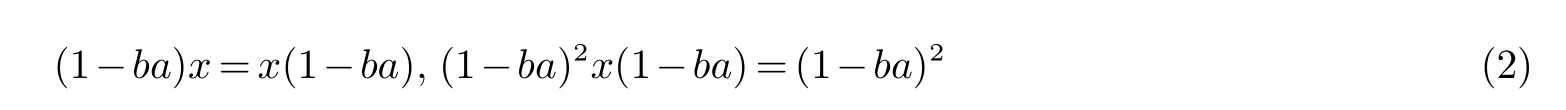
显然，环R 的由a,b,c 生成的子环是A 的（环）同态像,因此x 在此满同态下的像就是1−ba 在R 中的以Drazin指数为2 的Drazin 逆.

设I 是由cab−abc,ababcab−ababc−2abcab+abab+2abc+cab−2ab−c+1 生成的理想,这时A=Z a,b,c /I.设> 是{a,b,c} 上的deg-lex 序,且设c>b>a.令

且S={f,g}.下面我们要计算关于deg-lex 序> 的Gröbner-Shirshov 基.

其中w1=cababcab,w2=ababcab,w3=ababcababcab.下面我们计算这些合成.

即此合成平凡.

即此合成非平凡.我们令

即此合成平凡.

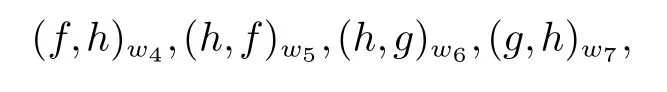
其中w4=cabababc,w5=abababcab,w6=abababcab,w7=ababcabababc.

现在我们计算这些合成：

所以S1={f,g,h} 是Gröbner-Shirshov 基.即我们证明了

引理2集合S1={f,g,h} 是在Z a,b,c 中关于deg-lex 序> 的Gröbner-Shirshov 基.

定理1方程(2) 在A 中有解.

证明由引理2 S1是Gröbner-Shirshov 基,所以由引理1 集合Irr(S1)是A 的一组Z−基,因此元素x ∈A 有如下表达式：

其中0 =αi∈Z,ui∈Irr(S1),1 ≤i ≤m,并且u1>u2>···>um.

由于在A 中有

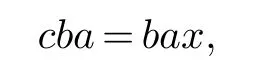
和

所以在A 中有

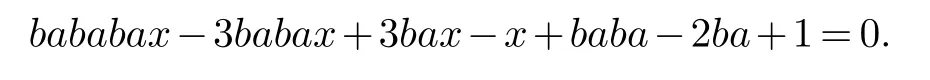
即

从而

把x 的表达式带进去得

由于bababau1是首项，因此bababau1/∈Irr(S1).因而u1=bcv,其中v 是a,c,c 的单项式.

我们令

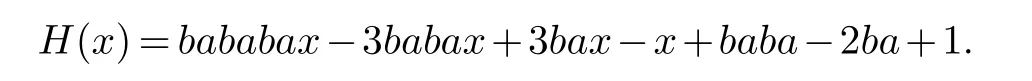
如果m=1,u1=bcv,则x=α1bcv.从而

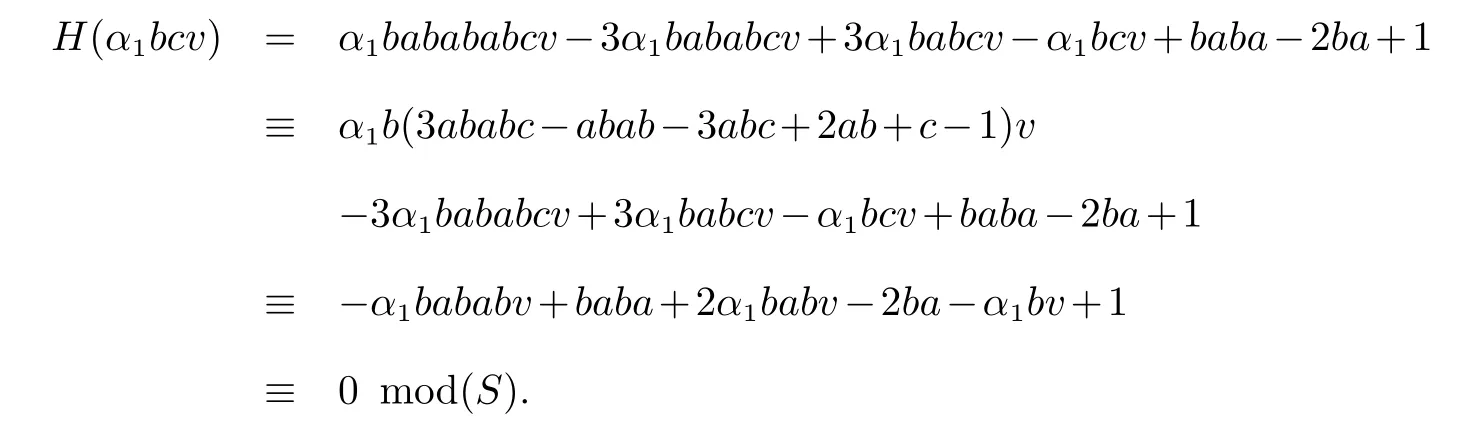
由于v ∈Irr(S1),我们有H(α1bcv) ≡0 mod(S),矛盾.所以m>1.因此

从而

如果|v|=0,即v=1,则bababau2是首项,因此bababau2/∈Irr(S1).从而u2=bc 或者u2=cab，与u1>u2,u1,u2∈Irr(S1) 矛盾.所以v =1.

如果|v|=1，则v=a,b,c.

我们考虑情况v=a,则u1=bca，且

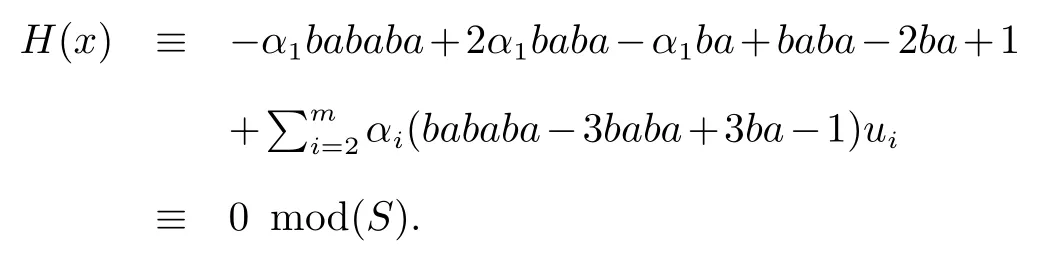
如果|u2|>0，则bababau2是首项，因此bababau2/∈Irr(S1).从而u2=bc.所以

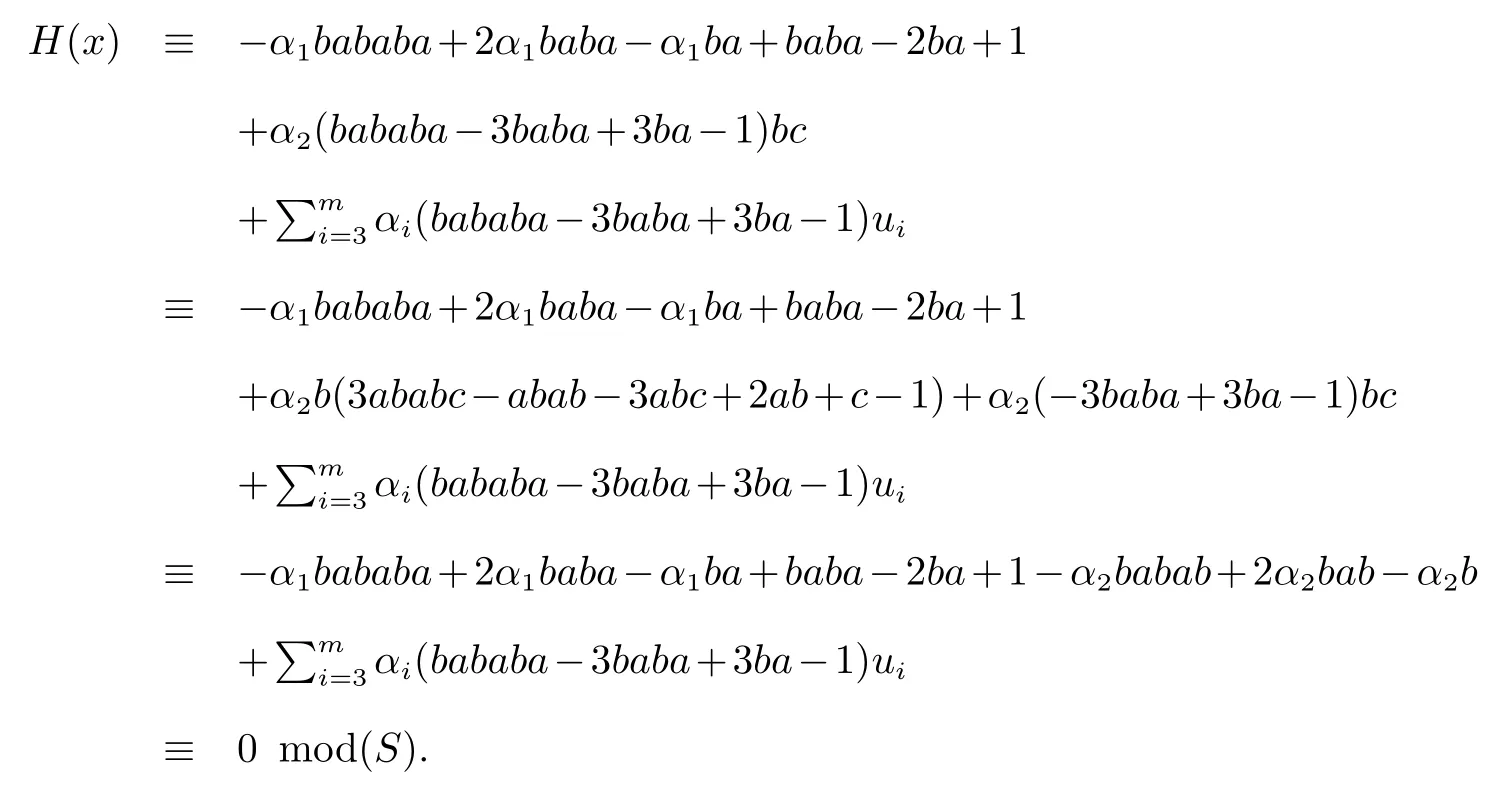
如果|u3|>0，则bababau3是首项，因此bababau3/∈Irr(S1).从而u3=bc，矛盾.所以u3=1.故

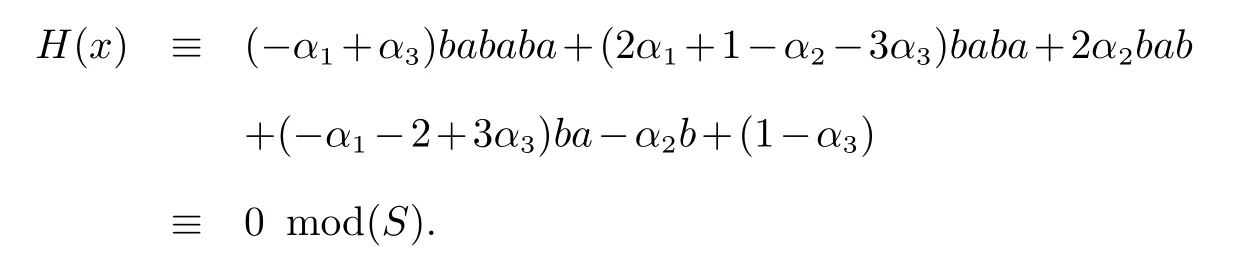
由于bababa,baba,bab,ba,b,1 ∈Irr(S1)，所以有方程组

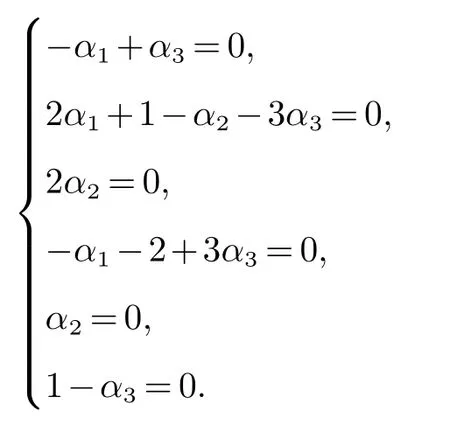
解得α1=α3=1,α2=0.所以x=bca+1.

3 结论

我们从1−ab 的逆出发，通过计算的方法得出1−ba 的逆，也就是说给出了一个当1−ab 可逆时，证明1−ba也可逆的构造性方法.