多事务兴趣度的度量方法*

阎 婷，吴文华，严丽娜，刘 晶

（国防科技大学信息通信学院试验训练基地，陕西 西安 710106）

0 引 言

常见的衡量关联规则相关度的方法有基于最小支持度和最小信任度阈值的支持度-置信度框架、基于Piatetsky-Shapiro提出的PS公式。第二种度量公式能去除大部分不相关的或负相关的关联规则，且有效简单，但在多事务兴趣度度量方面存在一定缺陷[1]。因此，现提出一种可以对多事务兴趣度进行度量的多事务兴趣度的度量方法，通过验证它是PS公式的扩展。

1 问题引入

例如，某一商场底层事务数据库中购买咖啡（事务C）、牛奶（事务D）、白糖（事务E）的统计况如图1所示。

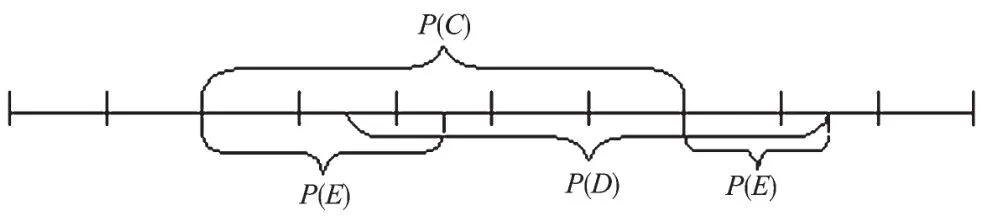
图1 购买咖啡、牛奶、白糖的统计

由 图1可 得 结 果：p(C)=50%，p(D)=50%，P(D)P(E)=0，说明事务C、D和E间的关联规则是无趣的，但是显然事务C和D、C和E、D和E、CD和E、CE和D、DE和C间均正相关，可见根据PS兴趣度公式推出的结论是不正确的。由上例可以看出，PS公式具有局限性，尤其是在判断二维以上关联规则的情况下。为了解决这样的问题，根据力学平衡原理引入多事务兴趣度度量的方法——多事务间诱导力的数学期望法。

2 多事务兴趣度算法描述

2.1 相关概念

定义1：诱导力。认为事务集S中的事务C1,C2,…,Cn是否同时出现是由某种力所决定的，把这种力命名为诱导力[2]，表示为：

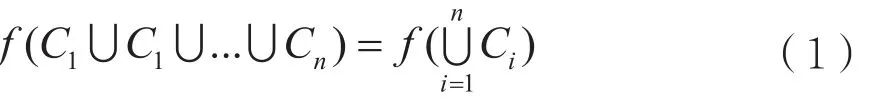
定义2：逆项集。对事务集S的Cni个i项子集进行任意排序，则第j项子集可表示为X(i,j)。设S(i,j)是X(i,j)与X(i,j)的所有元素的逆所组成集合的并集，即：

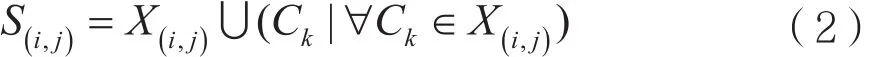
其中k∈(0,Cin)。

设Si是以S(i,j)为元素的集合，即：

为了方便，称Si是事务集S的i项逆项集，把S(i,j)中的第k个元素表示为S(i,j,k)。

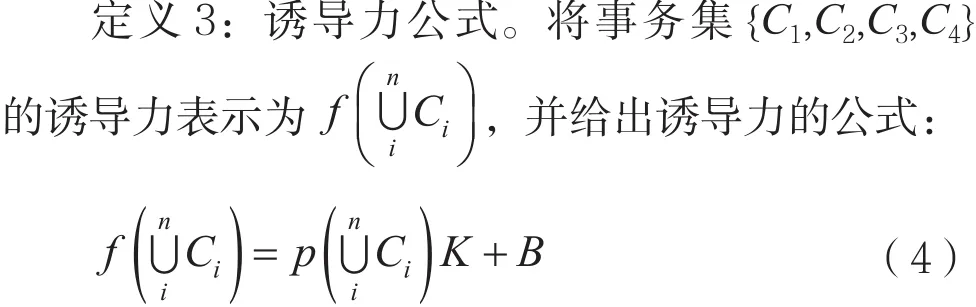
其中K称为诱导系数，满足以下条件[3]：

（1）K是常量，且K＞0；

（2）它的值因数据库的改变和事务C1,C2,…,Cn个数的改变而改变，在同一数据库中保持不变。

当事务C1,C2,…,Cn相互独立时，事务C1,C2,…,以诱导力公式为：

事务C1,C2,…,Cn所有诱导力的合力是事务集S中所有逆项集的诱导力数学期望之和，其中事务集S的所有逆项集共有Cn0+Cn1+…+Cin+…+Cnn-1+Cnn=2n个。

2.2 多事务兴趣度公式推导

当诱导力为0时，设f是事务C1,C2,…,Cn同时发生的正向诱导力。当诱导力小于0时，f是事务C1,C2,…,Cn同时发生的负向诱导力。

设给定诱导力合力的最小诱导力为阈值δ，则当诱导力合力小于阈值δ时，事务C1,C2,…,Cn正相关，即规则是有趣的；若诱导力合力大于阈值δ时，事务C1,C2,…,Cn负相关，即规则是无趣的；诱导力合力等于阈值δ，事务C1,C2,…,Cn不相关，即规则是无趣的。

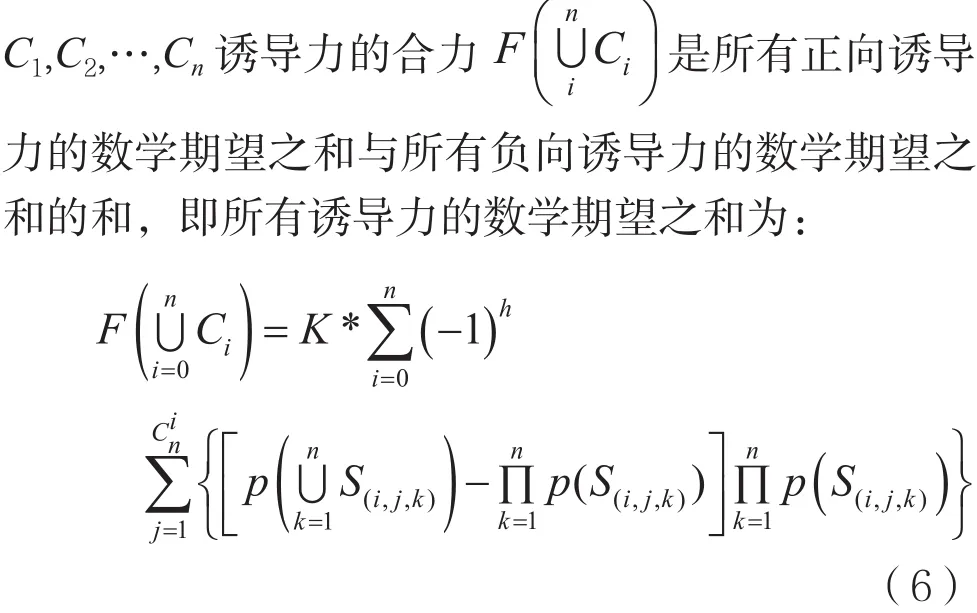
将式（6）等号两边同除以K，式（6）转化为：

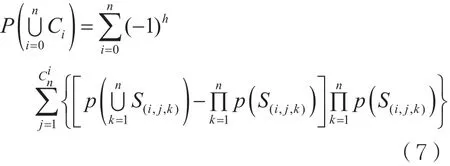
其中：

多事务兴趣度方法为式（7），有如下结论：

用户也可以根据自己的主观要求设定阈值进行挖掘或者测量，令ε=δ/K，ε是最小兴趣度的阈值。

3 算法应用及实现

3.1 应用

下面以多事务兴趣度公式分析给出购买咖啡（事务C）、牛奶（事务D）、白糖（事务E）的兴趣度。根据多事务兴趣度公式，求事务C、D、E的兴趣度如下：

因为P(CDE)=0.03＞ε=0.01，所以事务C、D、E是有兴趣的。

3.2 实现

本算法采用VC++作为开发环境进行测试，SQL SERVER存放数据库，且两个字段对数据进行存放。第一个字段存放记录的编号（相当于购买商品时小票的流水号），第二个字段存放每一条记录的所有商品名。采用Apriori算法挖掘频繁项集（最小支持度为0.3），用多事务兴趣度算法对挖掘出来的结果进行度量，结果如图2所示。

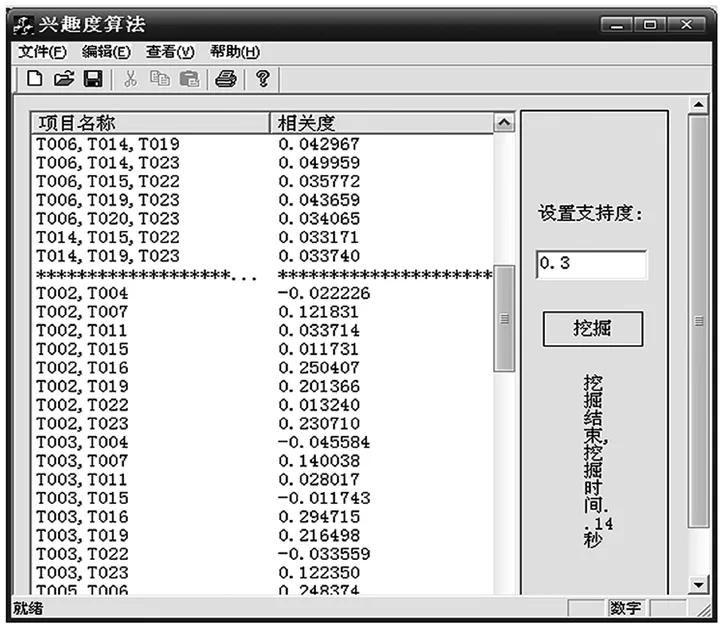
图2 多事务兴趣度度量结果

图2的结果显示，此方法不仅可以对二维关联规则进行度量，还可以对二维以上的关联规则进行度量。二维时，度量结果是PS公式的计算结果。所以，此法的适用性更强。

4 结 语

本文指出PS公式的缺陷和不足，引入逆项集和诱导力的概念，结合力学平衡原理等知识，提出了多事务客观兴趣度的度量方法。此方法综合考虑了规则准确度、相关度对规则兴趣度的影响，是PS公式的一个扩展。此方法不仅可以进行自挖掘，也可以用来对挖掘的关联规则进行度量。