极化码译码算法的改进与FPGA实现*

夏阁淞，葛万成

（同济大学中德学院，上海 200092）

0 引 言

自从香农在1948年发表了一篇代表着现代信息论开篇的文章后，通信技术就在不断快速发展。近几年，极化码在编解码领域中取得了突破性进展，从而激起了极化码理论研究的快速发展。Arikan Erdal于2008年提出极化码，并在对称的二进制无记忆信道及任意的连续无记忆信道中证明了极化码相较于Turbo码和LDPC码更能达到香农极限，且用极化码实现的通信系统能达到更高的通信带宽。所以，极化码是目前公认的“最好”的码。目前，极化码的译码实现方式主要有软件和硬件两种方式。软件的实现方式因CPU串行工作模式限制了译码速度的提升，而FPGA因其具有快速并行计算的能力能弥补这一缺陷。此外，极化码的递归结构能够实现资源共享并简化计算过程，这一特点表明极化码易于FPGA实现。

目前，关于极化码的译码算法主要有置信度传播（Brief Propagation，BP）算法、最大似然比（Maximum Likelyhood，ML）算法和连续删除（Successive Cancellation，SC）算法。这3种算法中，BP和ML算法由于在运算过程中涉及较多的乘除法运算，因此不利于FPGA实现；而SC算法在译码过程中主要通过加减和位运算实现，所以适于FPGA实现[1]。

1 极化码解码算法的改进

Arikan Erdal给出了极化码的一种解码算法，即最经典的连续删除译码算法。而极化码的建立过程即对极化信道的选择过程，实际上这种选择是以SC译码算法的性能为标准的。这是由于从极化信道转移概率式中可知，极化后的信道不是相互独立的：后面的信号信道的译码取决于前面序号的信道信息。这意味着必须保障前面的结果全部正确，极化码才能达到信道容量。但是，这要求码长必须足够长。

由于信道的极化过程，实际上是按照最优的SC译码算法执行的，因此对于极化码来说，只有这一类译码算法才能充分利用极化码的性能。随后诞生了简化的SC算法，即SSC译码算法。这几种方法将极化码的性能在延迟和正确性两个方面得到了提高。

SC译码算法的输出取决于两部分，分别是信道现在的接收信号和之前所有的判决。转移概率如下：

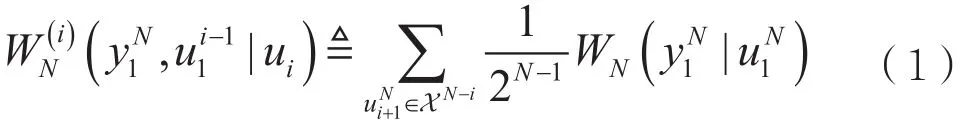
通过这两个信息可以计算目前正在判决的这一位的结果。判决时，如果解码器发现这一位是冻结比特，那么将直接判决为之前约定好的0或者1。如果解码器发现这一位是信息比特，需要通过计算u^i=0时和u^i=1的转移概率后得到对数似然比，最终得到判定结果。所以，从延迟上讲，该算法在一个时钟周期最多得出一位结果，解码速度较慢。

对数似然比在通信系统中的作用，一般是用做软解码。对数似然比的定义为：

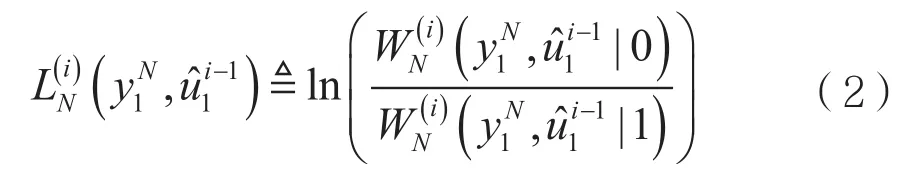
判决函数用L可以表示为：

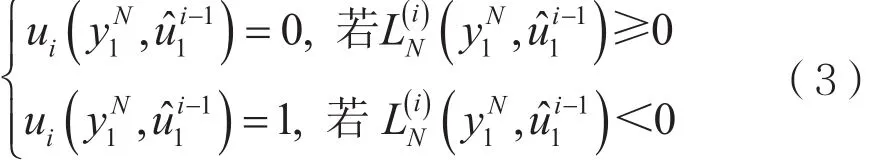
LLR的递归计算可以表示为：

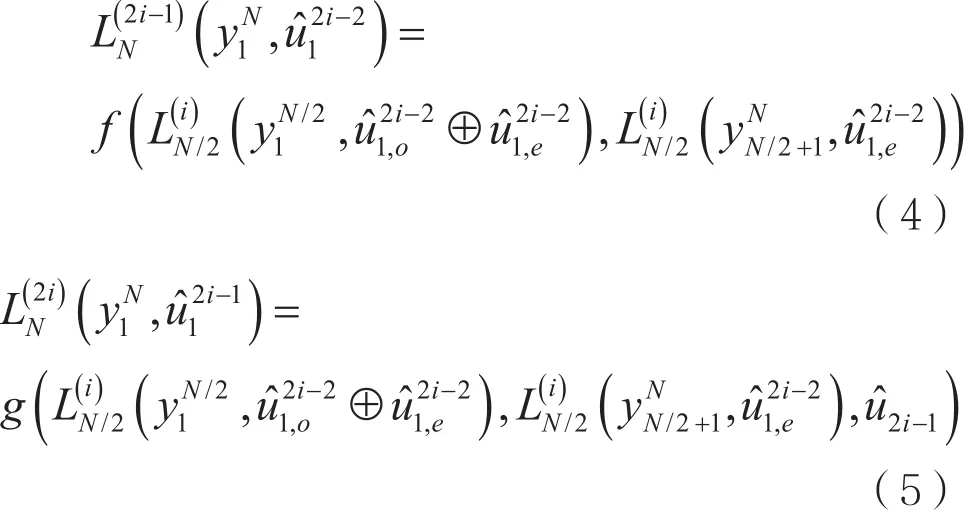
到了最底端即N=1时，是递归函数的出口，从而最终完成译码任务。

2 解码器的FPGA实现

2.1 FFT结构的SC解码器

FFT结构的SC解码器结构，如图1所示。该方案具有以下优点：由于这个结构并没有对硬件进行复用，而是使用了较多硬件，所以简化了控制结构，使得实现相对容易；不妨假设该方案不使用时钟信号，那么可以做到在一帧的情况下，相比于使用时钟信号控制的结构速度更快。但是，该结构也存在一些缺陷：由于该结构的硬件数量多且多数硬件是重复的，所以对硬件的利用率较低，带来了功率上的浪费（如果采用这个结构，那么可以每一个模块都会一直消耗功率消耗，且有相当多的功率是完全浪费的）；由于没有时钟信号的控制，该结构对于外界的噪声，抗干扰能力会大幅下降。如果采用D触发器这样的寄存器，那么只有在时钟信号有效的时候电路才真正工作，其他时候即便有噪声，也不会对电路结果造成影响；由于缺少控制信号，所以很难对电路的工作进度进行把控，且极化码的工作流程是按照步骤一步一步进行的，所以更加需要控制信号的加入，如果输入信号速度过快，超过了电路的处理速度，就会导致输出的信号产生错误。针对这些缺陷，需要大幅优化该结构。

图1 FFT结构的SC解码器结构

2.2 流水线的树结构SC解码器

流水线的树结构SC解码器，如图2所示。相比于FFT结构，它进行了一定优化：加入了时间控制模块。加入这个模块后，该编码器的过程可以实现控制。

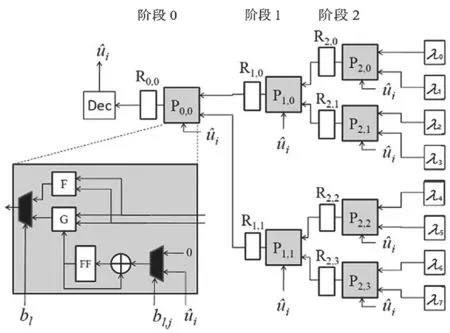
图2 流水线的树结构SC解码器

每经过一个时钟周期，该结构都会计算出一个值，这个值可能是F也可能是G。计算出来后，这个值会被保存到寄存器，以便后续计算时被使用。所以，该结构使用7个寄存器来存放。因为假设码长为1 024，那么按照这样的结构，需要1 024个寄存器保存之前计算的结果，显然非常浪费。为了优化空间，本文提出的结构中复用了存储LLR的寄存器来存储结果，可节省空间。

使用该结构另一个优点是，由于该结构的设计并不是针对某一种信道或一种冻结比特序列，而是对信道的类型不做限制，使得该结构具有了灵活的特性。事实上，这样的灵活带来的结果是对硬件的使用率不高，是该结构的两大缺点之一。本文提出的结构将针对某种特定的信道做出优化，大幅提高了硬件使用率。

该结构的第二个缺点是延迟高。从图2可以看出，每经过一个时钟周期，该结构只计算一步，且有很多不需要计算的部分。在本文提出的结构中，硬件电路会自动略过不需要计算的部分，减少了延迟。

2.3 F模块和G模块的改进设计

F模块和G模块的输入输出量，分别如图3和图4所示。

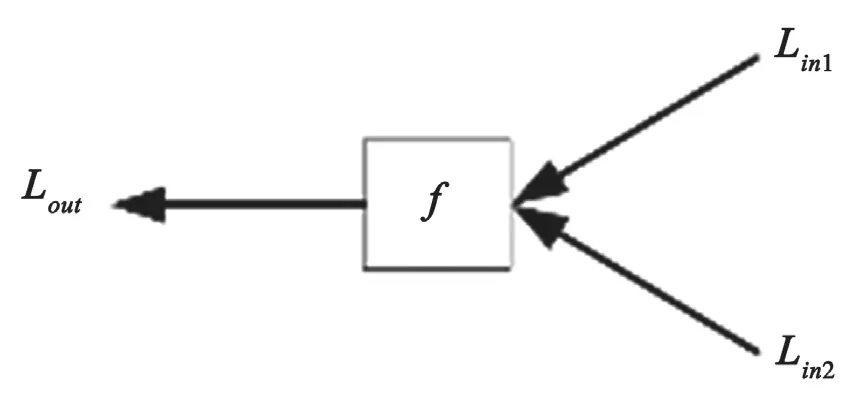
图3 F模块的输入输出量

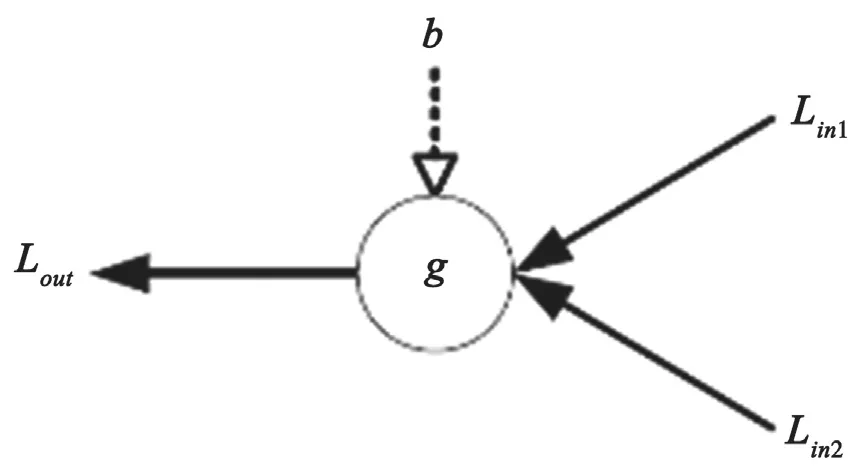
图4 G模块的输入输出量

F模块有2个输入，分别是LLR1和LLR2，也就是对数似然比，输出是一个值，把2个输入的符号相乘后取绝对值更小的：

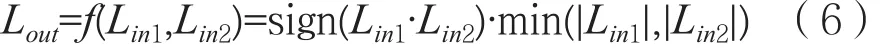
G模块则相对比较复杂，有3个输入量，除了2个LLR之外，还需要1个之前计算的u^。计算过程也更加复杂，涉及到乘法和加法。需注意，做乘法运算时，只是和-1乘，带来了优化的空间。

F模块和G模块一一对应，然后利用多路选择器选择当前工作是哪一个模块。传统设计的弊端在于F和G的数量永远相等，但是这并不是必须的。在某些特殊电路中，很有可能不需要那么多G，可能需要很多F。所以，本文提出的结构会把F和G模块完全独立。它们不相互影响，只在需要对方提供数据的时候才有交互[2]。

本文改进的F模块中，对于正负符号的判断，只提取了最高位。这是因为输入是量化后的8位信息，其中最高位是符号位，不需要在和0去比较，提高了运算速度[3]。同时，两个提取的符号位的乘法通过异或XOR实现，这在电路中的复杂度会远远小于一个乘法器。再将异或运算的结果即符号位去和更小的绝对值做最后的运算，得到F模块的输出。

在G模块中，论文采用的方法是多路选择器。将第一个输入信号的正负值输入到多路选择器中，根据第三个信号决定正负号后，将其与第二个信号求和。

F模块和G模块的设计思路，分别如图5和图6所示。

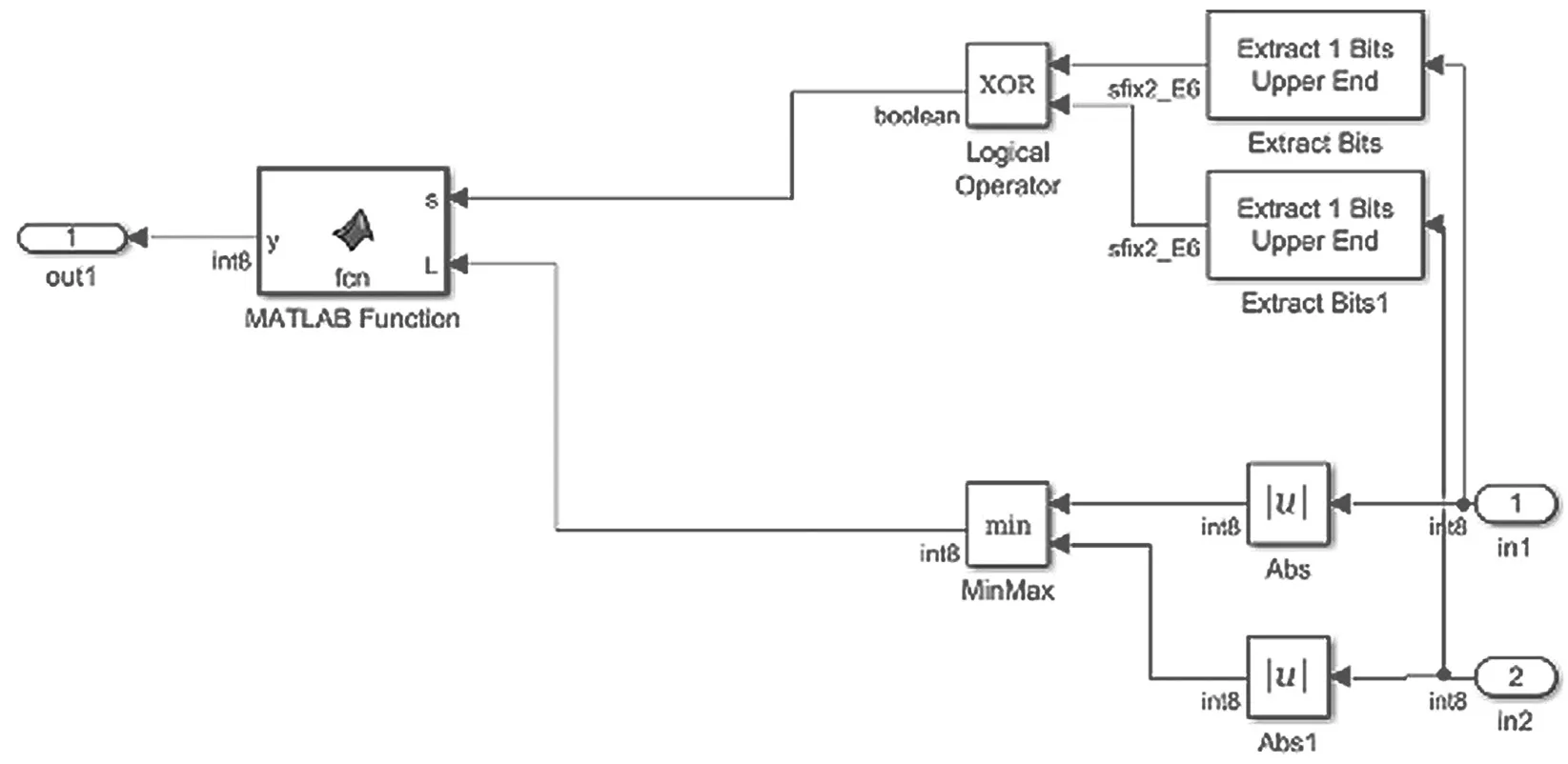
图5 matlab中F模块的设计思路

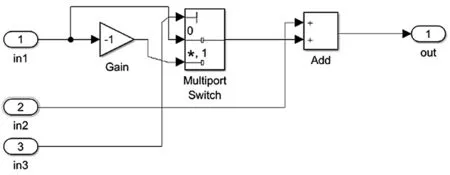
图6 matlab中G模块的设计思路

3 算法仿真与实验结果

函数f和g的计算涉及了乘法和除法，在FPGA中实现比较复杂。因此改进最小和算法，在对数域中用等价函数来代替，等价式为：

信道的输出和运算过程中的值都是浮点数，不利于在FPGA中实现，所以最后输出前需要进行硬裁决。

本文对该结构进行了实现，下面对码长为4的结果做出详细说明，如图7所示。

图7来自于testbench脚本，规定0时刻把输入给到电路，目的是首先测试电路是否需要一个上电准备过程，其次可以第一时间得到电路的输出。由图7可以得知，虽然在第一时间把输入的信号给了电路，但是电路并不能在第一时间把这个信号用来处理。这是由于在硬件内部，需要对该电压进行保持，其次需要经过缓冲器才可以把该信号交给电路内部处理，最后得到输出。经过测量得到，电路在第32 ns的时候准备完毕，然后进行下一步工作。

从图8可以看出，电路的输出信号正是符合预期地一个个相继输出，且结果通过和软件仿真的对比确保了正确性。

经过测量，直到最后一个输出结果显示完毕，也就是电路工作完毕的时间，是45.548 ns。这意味着从电路开始工作到结束，共花费了13.548 ns。

本文提出的译码器结构可以根据不同的冻结比特为自动生成对应电路，具有非常好的适应性和可拓展性。在硬件使用方面，相比于传统的译码器，硬件各个部分的使用大幅减小，包括LUT和FF。这其中的原因是该译码器减少了无用的F和G模块，同时复用了寄存器[4]。

此处对于码长为128的情况做出具体说明，如表1和表2所示。

表1 N=128时传统SC译码器的硬件消耗

表2 N=128时本文提出的SSC译码器的硬件消耗，R=0.25

对比表1和表2可以看出，在核心指标LUT和FF上，SSC结构具有明显优势，分别减少了63.9%和65.7%的硬件消耗，提高了性能。

本文提出的译码器的第二个优点是减少了译码器的延迟，可以大幅改善传统SC译码器延迟高的缺点，大大提高极化码的竞争力。

可以看出，随着冻结比特的比例不断增加，SSC译码器的性能不断提高。在25%的比特是冻结比特的时候，平均减小延迟55%；在50%的比特是冻结比特的时候，平均减小延迟53%；在75%的比特是冻结比特的时候，平均减小延迟62%，总平均提高57%。从图9可以看出，在实际的FPGA上运行结果符合预期。

图7 输入信号的实现后仿真结果

图8 输出端的信号变化情况

图9 在FPGA上的运行结果符合预期

本文实现的结构在对应的FPGA上，最短可以在时钟周期为7.968 ns的情况下工作。下面直接对吞吐量进行计算，结果如表3所示[5]。

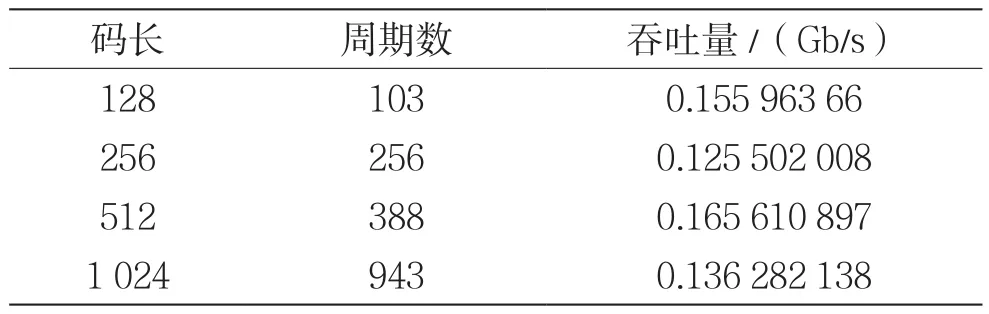
表3 不同码长情况下的吞吐量

4 结 语

本文提出的译码器结构可以根据不同的冻结比特自动生成对应电路，具有非常好的适应性和可拓展性。在硬件使用方面，相比于传统的译码器，对减小了各个部分的硬件使用，包括LUT和FF。究其原因，该译码器减少了无用的F和G模块，复用了寄存器。此外，这种结构能够减少译码器的延迟，可以大幅改善传统SC译码器延迟高的缺点，大大提高了极化码的竞争力。随着冻结比特的比例不断增加，译码器的性能不断提高，而本文采用的Matlab脚本可以针对不同冻结比特的特点，自动生成任意码长的对应结构，具有更高的灵活性。