HINOC2.0系统中高速LDPC译码器结构设计

赵 越，何大治，徐 胤，崔竞飞

（1.上海交通大学，上海 200240； 2.广播科学研究院，北京 100866）

下一代广播电视网（Next Generation Broadcasting，NGB）将网络平台的构建作为重点任务，超大流量的数据的快速传输问题是网络平台构建的难点之一[1]。同轴电缆宽带接入技术（High performance Network Over Coax，HINOC）[2-3]是一种新兴的信息传输理论，是解决高吞吐量信息快速传输难题的最佳方案。

HINOC2.0是HINOC1.0系统的升级版，对系统的各项性能提出了更高的要求，例如最大的覆盖范围达到1 000 m，最高的物理层传输速率1 Gbit/s，调制方式提高到4 096QAM，使用的低密度奇偶校验（Low Density Pari⁃ty Check，LDPC）码[4]要求有更强的纠错能力，误码平层要低于1E-12等。

1 LDPC码设计

LDPC纠错码是HINOC2.0系统中信道编码的核心部分，为满足HINOC2.0系统的性能要求，对LDPC码提出了基本参数和性能指标：

1）高码率，且误码平层要低于1E-12；

2）码长为1 920，3 840或5 760，LDPC码译码器的延时不能超过100 μs；

3）信息吞吐量达到1 Gbit/s。

在这些基本要求中，超高的吞吐量和很低的误码平层是技术难点。根据经验，对于一般的非规则码，要达到1E-12的误码平层是不可能的，而规则码则具有很低的误码平层，但其误码瀑布曲线比较平缓，因此可以适当减小不规则性来达到较低的误码平层和较陡峭的误码瀑布曲线，即选取准循环LDPC码（QC-LDPC）[5]。

其次，首先应达到吞吐量1 Gbit/s的要求，在此基础上即可计算出译码器的延时是否满足要求。若能满足1 Gbit/s的吞吐量要求，则对于不同的码长有不同的译码器延时，1 Gbit/s的输入数据能够进行正常译码，那么LD⁃PC译码器的延时就是N/109s，例如当码长N=5 760时，相应的延时为6 μs左右，当码长为N=1 920时，相应的延时为2 μs左右，均满足延时不超过100 μs的要求。

需要注意的是，上述对译码器延时的计算是假设1 Gbit/s的数据吞吐量是可以通过一个译码器来实现正确译码的，然而实际上，由于芯片时钟速率的限制，要实现Gbit/s数量级的译码速率，必须采用多个译码器并行译码的结构，设并行的译码器个数为M，则相当于每个译码器有1/M（Gbit·s-1）的数据吞吐量，因此其译码延时也将增大为原来的M倍。此时，若需要满足译码延时不超过100 μs的要求，需要对M的取值进行限制。并且，码长N越小，并行度M的最大值越大，因此对芯片处理速率的要求就越低。因此为尽可能在满足译码延时的条件下提高并行度M，选择码长为1 920的码字作为HINOC2.0系统中的LDPC纠错码，其码率为0.9。

2 译码器硬件结构设计

考虑到实际应用中，LDPC译码器的输入数据是码长长度的似然信息，因此只有当一个完整的码字全部输入到译码器之后才能开始译码，由于输入数据流一般都是连续的，因此需要额外的RAM来作为输入数据的缓存器。

乒乓RAM结构是工业界中LDPC译码器常采用的一种结构，译码算法为归一化的最小和算法。这种结构是将输入数据依次写入到2个RAM缓冲区，通过2个RAM的读和写的切换来实现数据的流水式传输和处理。其结构如图1所示。

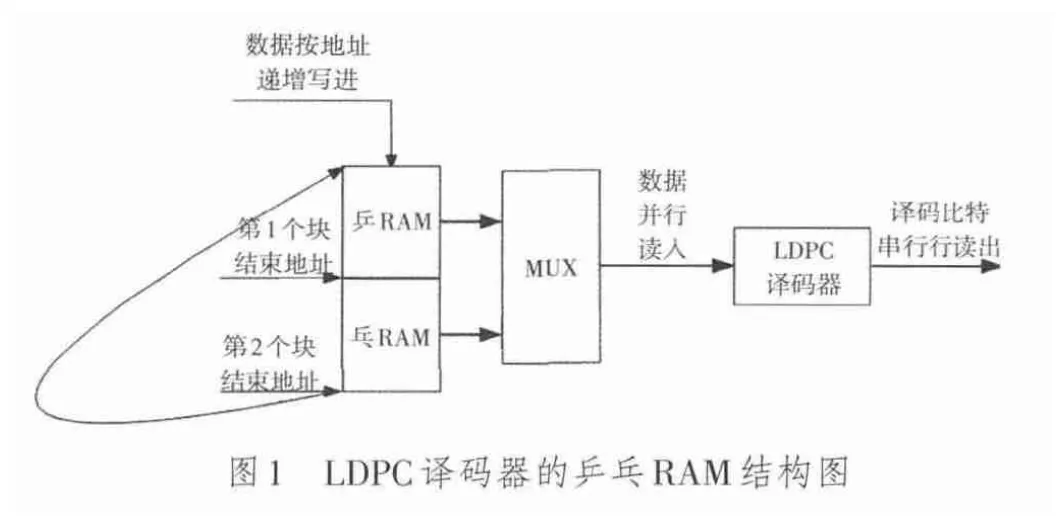
设译码器的迭代次数为X，LDPC码长为N，校验矩阵子块大小为q×q，输入数据速率为Rbit/s，译码器的芯片时钟频率为R2Hz，则约束关系为

式中：公式左边为该译码器每秒能完成译码的码字个数；右边为在输入数据速率为R时，每秒钟输入到译码器中的码字个数。目前高速的LDPC译码器芯片，其时钟频率可以达到200～300 MHz，为方便计算，不妨设为250 MHz，输入数据速率即HINOC2.0系统对LDPC译码器在吞吐量方面的要求，要求速率为1 Gbit/s，码长N为1 920，所设计的码字的子块大小为q×q=12×12，将这些参数代入式（1）可得，最大的迭代次数X为15次。

2.1 并行译码器结构

在一般情况下，译码器的时钟达不到250 MHz的速率，或者迭代次数要求多于15次，上述乒乓RAM的译码器结构便有了很大的局限性。

针对乒乓RAM的局限性，本文提出了一种多个译码器并行的结构，其结构图如图2所示。

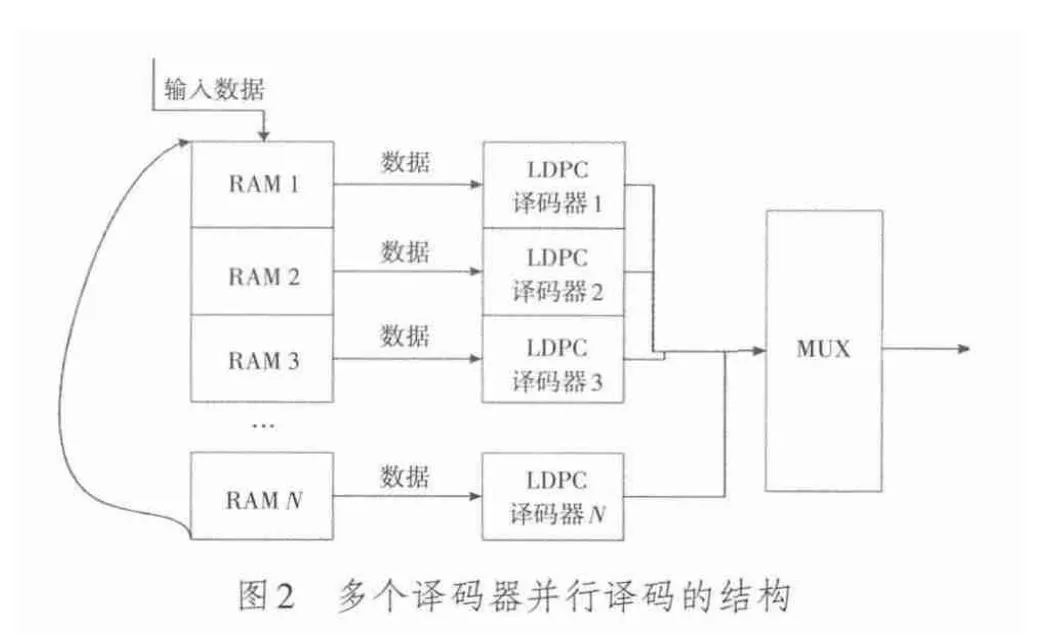
工作流程为：首先将输入数据按照地址递增的顺序快速写入RAM中，当地址累加到第二个RAM块开始时，那么输入的LLR数据正好为一个LDPC码字长度，将第一个RAM数据读入LDPC译码器1并开始译码，输入数据继续写入RAM 2中，依次循环，直到地址累加到第N个RAM的结束地址，则将RAMN的数据读入译码器N进行译码。之后输入数据的写入地址则回到RAM 1的起始地址，此时要求译码器1已经完成译码，将译码器1的结果通过MUX输出，之后依次循环进行RAM 2，RAM 3，…，RAMN的数据写入和译码。

可以看到相对于图1中的乒乓译码器结构，图2中并行译码器结构使得每一个译码器可以花费的译码时间增加了（N-1）倍，因此这种结构可以解决由于高吞吐量或者高的迭代次数而带来的译码时间不足的问题。其中N的选取可以通过式（2）求得

式中：T1为一个LDPC块的数据写入一个RAM所需要的时钟周期的个数；T2为译码器完成一个LDPC码字译码所需要的时钟周期的个数。设数据传输速率为R，码长为n，芯片处理时钟为R2，那么T1可以表示为

将式（3）代入式（2），可得N的决定公式为

需要注意的是，译码器1的译码时间其实可以再增加一个写RAM 1所需要的时间，换个角度考虑，即其实可以节省一个译码器，那么当每一次输入数据完成一次循环，从RAMN回到RAM 1时，RAMN的数据读入到译码器1中进行译码，RAM 1的数据所传入的译码器则会向下移动一个，RAM 2，RAM 3也是如此。进一步考虑，如果译码器的译码速率可以再快一些，当输入数据写完RAM（N-X）时，译码器1已经完成译码，那么则可以节省（X+1）个译码器。

2.2 并行译码器结构的改进

图2中的译码器结构有一定的缺点，如N个译码器是相同的逻辑资源结构，虽然其在结构上是并行译码，但译码并不是同时进行，所以并不能很好的将多个译码器行操作、列操作的信息存取所需要的RAM整合到一起，也不能将多个译码器的读写地址的逻辑进行整合。本节提出一种改进的结构，使得多个译码器译码时RAM资源能进行整合，并且有比较统一的读写逻辑，如图3所示。

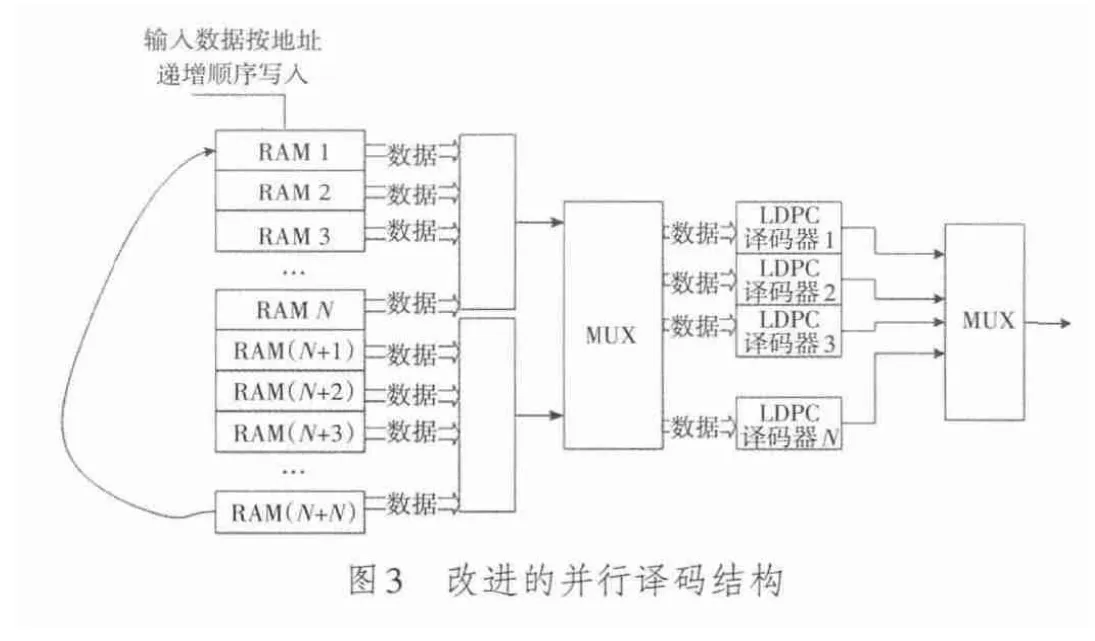
事实上，图3所示的译码器结构是图1乒乓RAM结构和图2并行结构的结合。当数据写满RAM 1～RAMN时，将前N个RAM中的数据同时MUX，并且分配到译码器1到N，同时进行译码操作；同时数据开始写RAM（N+1），而当输入数据写满RAM（N+1）到RAM（N+N）时，此时必须保证前N个RAM的译码已经完成，再将后面N个RAM的数据读入到MUX进而分配到相应的译码器中同时进行译码操作，输入数据回到RAM 1继续进行数据写入，依次循环。

这样的结构使得译码器可以同时进行并行译码，其RAM资源可以共用，并且译码器的读写逻辑能够一致，不会出现时钟错位的情况。

另一种译码器硬件结构如图4所示，适用的情况为当译码器的外部RAM有限，但是仍然要求有较多的迭代次数。上述结构中，迭代次数的最大值为

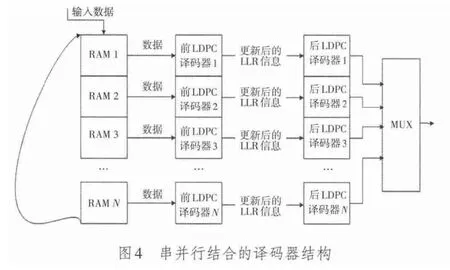
考虑到译码器的迭代过程中，每个变量节点的信息为更新后的LLR信息，因此可以在译码器后再接一个译码器，前面的译码器不需要进行译码判决，只需将迭代X次后的变量节点的LLR信息传输到后面的译码器即可。

可以看出，这样的译码器结构使得译码等效迭代次数增多为2X，因此会有更好的译码性能。需要注意的是，在译码过程中，前后两个译码器所译的码字其实不是同一个码字，而是输入码字流中相隔（N-1）的码字，例如前面的译码器码字为（N+1）时，相应的后面的译码器是第1个码字，当后面的译码器进行X次迭代后，前面译码器将输出迭代X次后变量节点的LLR信息输入到后面的译码器。

2.3 各种译码器结构的硬件资源分析

译码器所占用的硬件资源主要分为三种，即存储输入数据所需要的缓存RAM，称之为外部RAM资源，译码器进行行操作和列操作时更新的节点信息的存储RAM，称之为内部RAM，以及进行节点间传递信息的计算所需要的逻辑资源。在此，由于逻辑资源随译码算法的不同而不同，因此只给出外部RAM和内部RAM资源的分析。

统一规定用于定点化LLR信息的比特位数为 f=8，码长为1 920，P为H矩阵中“1”的个数。上述各种结构所占用的硬件资源以及适用场合如表1所示。

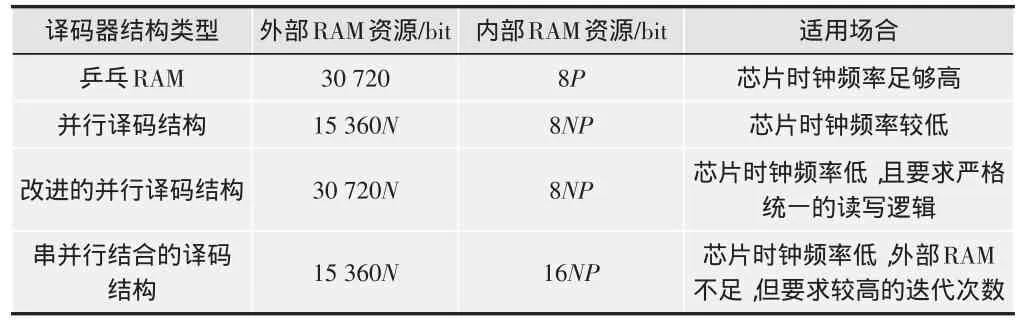
表1 几种译码器结构的硬件资源分析

2.4 各种译码器结构的硬件资源分析

为说明迭代次数对译码器译码性能的影响，图5是不同迭代次数下，某一HINOC2.0备选码字的性能仿真结果。

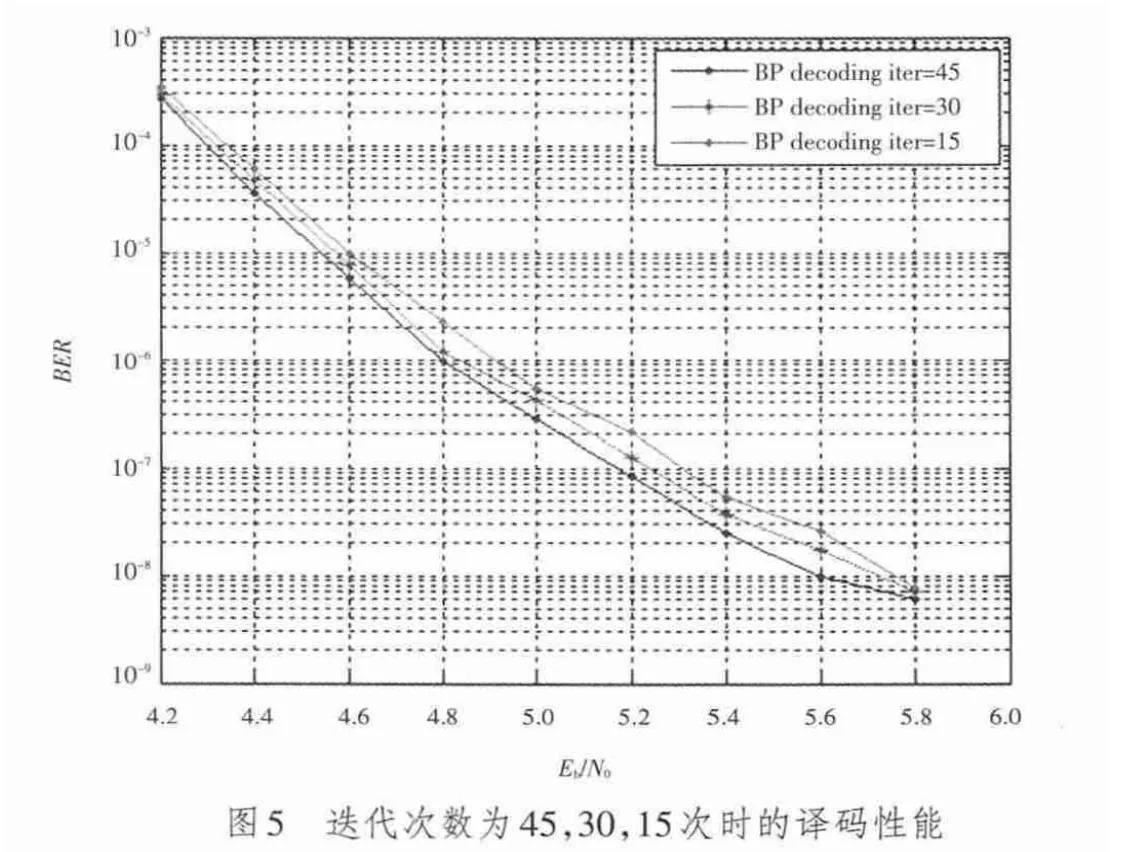
可以看出，迭代15次的译码性能并不会比45次相差很多，因此在一般情况下15次迭代完全可以满足译码性能的要求，可以将15次迭代作为HINOC2.0中LDPC译码器设计的最优迭代次数。

3 小结

本文基于HINOC2.0系统对LDPC码译码器吞吐量达到1 Gbit/s和译码延时不超过100 μs的要求，给出了3种不同的译码器硬件结构，可为译码器的硬件实现提供参考，并给出了硬件资源分析和仿真结果作为理论依据。LDPC码的设计是HINOC2.0系统的瓶颈之一，目前已有多家研究机构在LDPC码的设计上投入了大量的精力，LDPC码译码器在硬件上的实现有待于进一步研究。

：

[1]刘晓雪，章文辉.浅谈下一代广播电视网（NGB）[J].电视技术，2009，33（S2）：150-152.

[2]欧阳峰，崔竞飞，赵玉萍，等.HINOC同轴电缆接入系统技术方案[J].广播与电视技术，2011（10）：34-38.

[3]欧阳峰，崔竞飞.HINOC技术概述和进展[J].电视技术，2011，35（12）：11-13.

[4]GALLAGER R.Low-density parity-check codes[J].IRE Trans.In⁃form Theory，1962（1）：21-28.

[5]KOU Y，LIN S，FOSSORIER M.Low density parity checkcodes：con⁃struction based on finite geometries[C]//Proc.IEEE Globecom 2000.San Francisco，CA：IEEE Press，2000:825-829.